координаты »
найти наибольшее и наименьшее значение функции - страница 2
1. Найди корни уравнения 1/2*x^2=x+4.
(Корни уравнения запиши в возрастающем порядке, если корней нет, поставь −)
Ответ: x1= ;x2=
2. Без построения графика функции, определи в каких четвертях расположен график функции y=3,8*x^2.
(Четверти запиши арабскими цифрами)
3. Найди наибольшее значение функции y=6*x^2 на отрезке [0;1].
Ответ: y (наибольшее)=
Решение: .1
1/2*x²=x+4/*2
x²-2x-8=0
x1+x2=2 U x1*x2=-8
x1=-2 U x2=4
Ответ x1=-2,x2=4
2
y=3,8x²
a>0⇒график расположен в I и во II четверти
3
y=6x²
y(0)=6*0=0
y(1)=6*1=6
Ответ унаиб=6
1. Найдите наибольшее и наименьшее значения функции у = х6 на отрезке [–1; 2].
2. Сколько корней имеет уравнение –0,5х4 = х – 4?
3. Постройте и прочитайте график функции:
4. Найдите наибольшее и наименьшее значения функции у = (х – 2)3 +
+ 4 на отрезке [0; 3].
Решение: 1. Найдите наибольшее и наименьшее значения функции у = х6 на отрезке [–1; 2].
Минимум х=0 у=0
Максимум х=2 у=64
2. Сколько корней имеет уравнение –0,5х4 = х – 4?
-2=х-4
х=2 один корень
3. Постройте и прочитайте график функции:
Какой?
4. Найдите наибольшее и наименьшее значения функции у = (х – 2)3 +4 на отрезке [0; 3].
у=3х-6+4=3х-2
у=3х-2
Минимум при х=0 у=-2
Максимум при х=3 у=71 Найдите наибольшее и наименьшее значение функции у=х в восьмой на отрезке [-2,1]
2. сколько корней имеет уравнение 0,5х в кубе =2- х
3 постройте график и прочитайте функцию.
4 Найдите наибольшее и наименьшее значение функции
Решение: 1. y наибольшее= 256y наименьшее =1
2. один корень (графически попробуй сделать)
3. построй графики, по ним все наглядно видно, могу сказать что в первом икс принадлежин ( - ∞; 0) U (0;+ бесконгечности)
во втором же D=(-бесконечности;+ бесконечности)
4. y наибольшее= 12
y наименьшее =-3
////////////////////////////////////////////////////////////////////////////
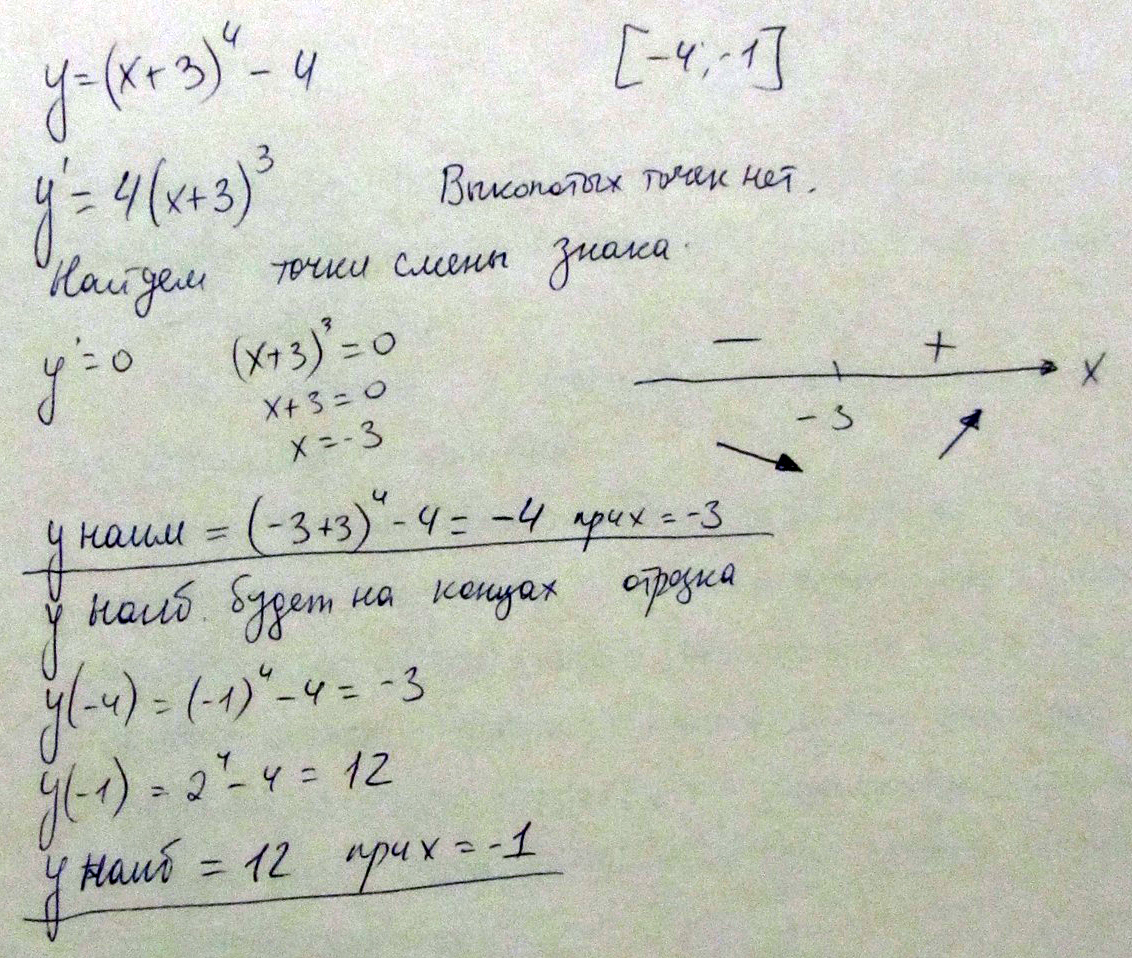
Функция y=f(x) задана графиком. Укажите для этой функции: а) область определения; б) нули; в) промежутки знакопостоянства; г) промежутки возрастания(убывания); д) наибольшее и наименьшее значение функции; е) область изменения.
Решение: А) от -4 до 3
б) х = -3; х = -1; x = 2
в) у > 0 при х Е [-4; -3), (-1; 2)
y < 0 при x E (-3; -2), (2; 3]
г) возрастает на x E (-2; 1)
убывает на x E (-4; -2), (1; 3)
д) наибольшее у = 3
наименьшее у = -2
е) [-2; 3]А)D(y)∈[-4;3]
б)x=-3 x=-1 x=2
в)y<0 x∈(-3;-2) U (2;3]
y>0 x∈[-4;-3) U (-1;2)
г) возр х∈(-2;1)
убыв х∈[-4;-2) U (1;3]
д)ymax(1)=3
ymin(2)=-2
e)E(y)∈[-2;3]Функция y=f(x) задана графиком. Укажите для этой функции: а) область определения; б) нули; в) промежутки знакопостоянства; г) промежутки возрастания(убывани
я); д) наибольшее и наименьшее значение функции; е) область изменения.
Решение: А) Область определения - это те иксы, на которых f определена. По картинке хорошо видно что это промежуток [-3; 4].
б) Нули - это решения уравнения f(x) = 0 или y = 0, то есть пересечения графика с осью Oy. По графику видно, что это точка 1.
в) Промежутки знакопостоянства следующие: [-3;1] и [1;4]. На каждом из них функция имеет постоянный знак (находится выше или ниже оси oX). На первом - она неотрицательна, на втором - неположительна.
г) По картинке видно, что функция возрастает (график идёт вверх) на промежутке [-3; -1], затем убывает на [-1; 2] и вновь возрастает на [2;4].
д) Наибольшее и наименьшее значения функции: 2 и -2 соответственно, это можно понять, посмотрев на ось Oy.
е) Область изменения (правильнее называть её множеством значений) функции - это те y, которые принимает f(x) при любом x из области определения. По картинке видно, что это промежуток [-2;2], опять смотри на ось Oy.


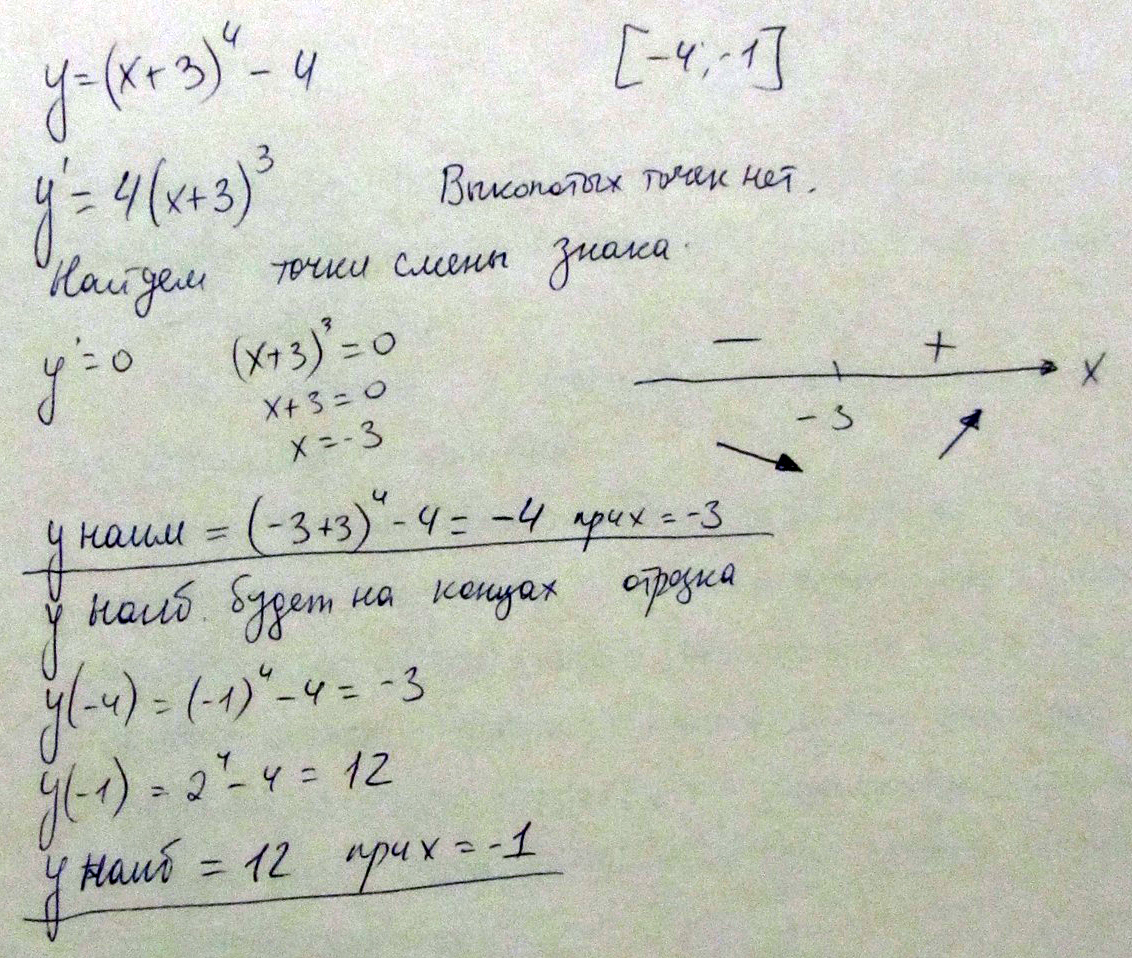
 Декартова система координат
Пусть в пространстве заданы две различные произвольные точки О и М, и пусть одна из них, например точка О, выбрана в качестве начальной. Тогда вектор \(\vec{OM}\) называется радиус-вектором точки М относительно точки О (рис.).
Пусть в пространстве задана точка О и некоторый базис e1, e2 , e3. Совокупность этого базиса и точки О называется декартовой системой координат О,...
Декартова система координат
Пусть в пространстве заданы две различные произвольные точки О и М, и пусть одна из них, например точка О, выбрана в качестве начальной. Тогда вектор \(\vec{OM}\) называется радиус-вектором точки М относительно точки О (рис.).
Пусть в пространстве задана точка О и некоторый базис e1, e2 , e3. Совокупность этого базиса и точки О называется декартовой системой координат О,... Выбором прямоугольной декартовой системы координат устанавливается взаимно однозначное соответствие между точками плоскости и упорядоченными парами действительных чисел. Это означает, что каждой точке плоскости соответствует единственная пара чисел и каждой упорядоченной паре действительных чисел соответствует единственная точка.
Выбор той или иной системы координат ничем не ограничен и определяется в каждом конкретном случае только соображениями удобства. Часто одно и то же множество приходится...
Выбором прямоугольной декартовой системы координат устанавливается взаимно однозначное соответствие между точками плоскости и упорядоченными парами действительных чисел. Это означает, что каждой точке плоскости соответствует единственная пара чисел и каждой упорядоченной паре действительных чисел соответствует единственная точка.
Выбор той или иной системы координат ничем не ограничен и определяется в каждом конкретном случае только соображениями удобства. Часто одно и то же множество приходится...