координаты »
найти наибольшее и наименьшее значение функции - страница 4
Задана функция y=-x^2 + 2 x + 3. Постройте его график и с помощью графика найдите:
1) промежутки, в которых график возрастает.
2) промежутки, в которых график убывает.
3) наибольшее значение функции
4) при каких значениях x y<0
Решение: 1. способ (без производной) График функции является квадратичной параболой. Так как коэффициент при х² отрицателен, то ветви параболы направлены вниз. Перепишем уравнение в виде y=-(x^2-2x-3)=-((x-1)^2-4)=4-(x-1)^2. Второе слагаемое либо положительно, либо обращается в 0 (при x=1). Отсюда ясно, что наибольшее значение функции достигается при х=1: у(1)=4. При x<4 функция возрастает, при x>4 функция убывает. Функция обращается в 0 при (x-1)^2=4, т. е. при x=3 и при x=-1, при x<-1 и при x>3 функция отрицательна (y<0).
2 способ. Производная y’=-2x+2=0 при x=1. Так как при x<1 y’>0, то при x<1 функция возрастает. Так как при x>1 y’<0, то при x>1 функция убывает. Так как при переходе через х=1 знак производной меняется с + на - то точка x=1 - точка максимума, причём у(1)=-1+2+3=4
1. Найдите значение производной функции f(x)=7x^3-2x^2+3 в точке х =1
2. Найдите наибольшее и наименьшее значение функции f(x)=2x^3-6x^2+7 на отрезке [1;4]
3. Исследуйте функцию f(x)=x^3+3x^2+2 и постройте ее график
Решение: 1. f’(x) = 21x^2 - 4x
f’(1) = 21*1^2 - 4*1 = 21 - 4 = 17.
2. f’(x) = 6x^2 - 12x.
6x^2 - 12x = 0, 6x(x - 2) = 0, x = 0, x = 2 - критические точки. Первая точка не принадлежит отрезку [1; 4].
f(2) = 2*2^3 - 6*2^2 + 7 = 16 - 24 + 7 = -1.
f(1) = 2*1^3 - 6*1^2 + 7 = 2 - 6 + 7 = 3.
f(4) = 2*4^3 - 6*4^2 + 7 = 128 - 96 + 7 = 39.
max f(x) = f(4) = 39, min f(x) = f(2) = -1.
3.
а) Область определения функции - вся числовая прямая.
Проверим функцию на чётность/нечётность:
f(-x) = (-x)^3 +3*(-x)^2 + 2.
f(-x) =/ f(x), f(-x) =/ -f(x), значит, данная функция не является чётной или нечётной. Функция непериодическая.
б) Асимптоты, поведение функции на бесконечности.
Так как функция непрерывна, то вертикальные асимптоты отсутствуют.
k = lim f(x) = lim x^3 + 3x^2 + 2 = +беск.
x-> беск x x
Нет и наклонных асимптот.
Выясним, как ведёт себя функция на бесконечности:
lim x^3 + 3x^2 + 2 = + беск.
x-> +беск
Если идём вправо, то график уходит бесконечно вверх, если влево – бесконечно вниз.
Таким образом, функция не ограничена сверху и не ограничена снизу. Учитывая, что у нас нет точек разрыва, становится понятна и область значений функции - любое действительное число.
в) Нули функции и интервалы знакопостоянства.
Пересечение графика с осью У:
x = 0 -> f(0) = 2.
Пересечение графика с осью X:
f(x) = 0 -> x^3 + 3x^2 + 2 = 0.
Такое уравнение имеет, как минимум, один действительный корень, и чаще всего этот корень иррационален.
г) Возрастание, убывание и экстремумы функции.
Найдём критические точки: f’(x) = 3x^2 + 6x.
3x^2 + 6x = 0, 3x(x + 2) = 0, x = -2, x = 0.
+ - +
-+-+-
-2 0
Следовательно, функция возрастает на (-беск; -2)u(0; +беск) и убывает на (-2; 0).
f(-2) = -8 + 12 + 2 = 6 - максимум.
f(0) = 0 + 0 + 2 = 2 - минимум.
д) Выпуклость, вогнутость и точки перегиба.
Найдём критические точки второй производной:
f’’(x) = 6x + 6 = 0. x = -1.
Определим знаки f’’(x):
- +
-+-
-1
График функции является выпуклым на (-1; +беск) и вогнутым на (-беск; -1). Вычислим ординату точки перегиба: f(-1) = -1 + 3 + 2 = 4.
е) Найдем дополнительные точки, которые помогут точнее построить графикПостройте график линейной функции y= -2х + 1/ С помощью графика найдите: а) наименьшее и наибольшее значения функции на отрезке [-1; 2]; б) значение переменной х, при которых грфик функции расположен ниже оси Ох.
Решение: Построить чисто физически не могу, но чем подсказать смогу, то и напишу.х 0 1
у 1 -1
(это мы отметили точки, через которые проходит график)
а) Чтобы найти наименьшее и наибольшее значение функции (у), можно без графика определить методом подставления, т. е.:
y наименьш. = -3
у наиб. = 3
б) Не совсем понял вопрос, если нужно выяснить значение функции (у), когда она меньше 0, то подставляем х или ищем по графику, получится:
у меньше 0, при х равном или больше 1
Как смог уж :)
Постройте график линейной функции y=1/2x-2 С помощью графика найдите: Наименьшее и наибольшольшее значение функции на отрезке [-2;4] Значение переменной
x, при которых y<0.
Решение: Линейная функция, график - прямая, строим по двум точкам, например (0;-2); (2;-1); на отрезке yнаим=-3, унаиб=0, y<0 при x<4
Для построения графика линейной функции нужно взять любой х (бери в пределах разумного), подставляете его в формулу, считаете y, получается точка, отмечаете её в декартовой системе координат (обычная система XoY), то же самое делаете для второй точки, соединяете их в системе координат, подписываете полученный графикПостройте график линейной функции у= 1/2х -2.
С помощью графика найдите:
А) наименьшее и наибольшее значения функции на отрезке [-2,4];
Б) значения переменной х, при которых у меньше или равно 0.
Решение: X=0, то y=-2
X=4 то y=0
внизу Я добавил график
a) [ -2 ; 4 ]
у мин = -3
Y макc = 0
б ) y ≤0 (-∞ ; 4]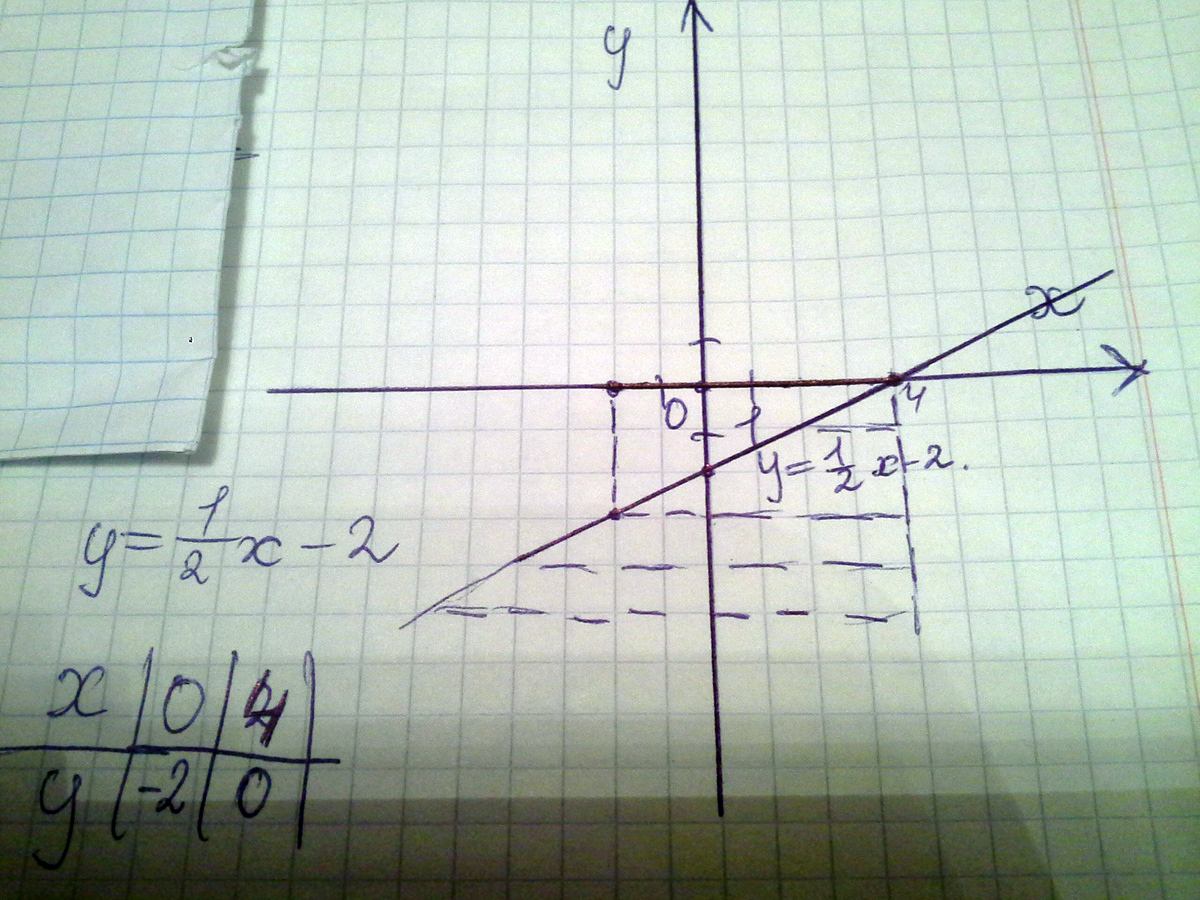


 Декартова система координат
Пусть в пространстве заданы две различные произвольные точки О и М, и пусть одна из них, например точка О, выбрана в качестве начальной. Тогда вектор \(\vec{OM}\) называется радиус-вектором точки М относительно точки О (рис.).
Пусть в пространстве задана точка О и некоторый базис e1, e2 , e3. Совокупность этого базиса и точки О называется декартовой системой координат О,...
Декартова система координат
Пусть в пространстве заданы две различные произвольные точки О и М, и пусть одна из них, например точка О, выбрана в качестве начальной. Тогда вектор \(\vec{OM}\) называется радиус-вектором точки М относительно точки О (рис.).
Пусть в пространстве задана точка О и некоторый базис e1, e2 , e3. Совокупность этого базиса и точки О называется декартовой системой координат О,... Выбором прямоугольной декартовой системы координат устанавливается взаимно однозначное соответствие между точками плоскости и упорядоченными парами действительных чисел. Это означает, что каждой точке плоскости соответствует единственная пара чисел и каждой упорядоченной паре действительных чисел соответствует единственная точка.
Выбор той или иной системы координат ничем не ограничен и определяется в каждом конкретном случае только соображениями удобства. Часто одно и то же множество приходится...
Выбором прямоугольной декартовой системы координат устанавливается взаимно однозначное соответствие между точками плоскости и упорядоченными парами действительных чисел. Это означает, что каждой точке плоскости соответствует единственная пара чисел и каждой упорядоченной паре действительных чисел соответствует единственная точка.
Выбор той или иной системы координат ничем не ограничен и определяется в каждом конкретном случае только соображениями удобства. Часто одно и то же множество приходится...