координаты »

определите координаты точек пересечения графиков

  • 1. Решите систему уравнений: xy=-10 x-y=7 2. Вычислите координаты точек пересечения графиков уравнений: x^2-y^2=13 и x+y=-5


    Решение: 1. x-y=7

      x=7+y

    2. xy= -10

      y(7+y)=-10

      y^2+7y=-10

      y^2+7y+10=0

      D=7^2-4*10*1=49-40=9.

      y1=(-7+3)/2=-2.

      y2=(-7-3)/2=-5,5.

    3. x=7+y

      x1=7+(-2)=5.

      x2=7+(-5,5)=1,5.

  • №1 Дана функция у=6х+19 а) у=? х=0,5

    б) х=?у=1 в) А(-2;7)
    №2 Построить график функции(только ответы, сам график не нужен) у=2х-4 б) у=? х=1,5
    №3 В одной системе координат построить графики функции(только ответы, сам график не нужен) у=-2х у=3
    №4 Найти координаты точек пересечения графиков функций у=47х-37 у=13х+23
    №5 Задать формулой линейную функцию, график которой параллелен прямой у=3х-7 и проходит через начало координат


    Решение: #1

    Tam nado prosto podstavit v uravneniye X (esli dano) ili Y (esli dano) i naiti to, chego ne hvataet.

    naprimer :

    y = 6X + 19

    y = 6* 0,5 + 19

    y = 3 + 19 = 22

    #2

    tut toje samoe

    №1

    Дана функция 

    у=6х+19

    а) у=? х=0,5 y=6*0.5+19=3+19=22

    б) х=?у=1 6x+19=1 6x=-18 x=-3

    в) А(-2;7) 6*(-2)+19=-12+19=7 проходит

    №2

    Построить график функции(только ответы, сам график не нужен)

    у=2х-4

    б) у=? х=1,5 y=2*1.5-4=3-4=-1

    №4

    Найти координаты точек пересечения графиков функций

    у=47х-37

    у=13х+23

    47х-37=13х+23 34x=60 x=60/34=30/17 y=13*30/17+23=390/17+23=

    №5

    Задать формулой линейную функцию, график которой параллелен прямой у=3х-7 и проходит через наяало координат

    параллельно прямой значит к=3

    проходит через начало координат y=3x

       

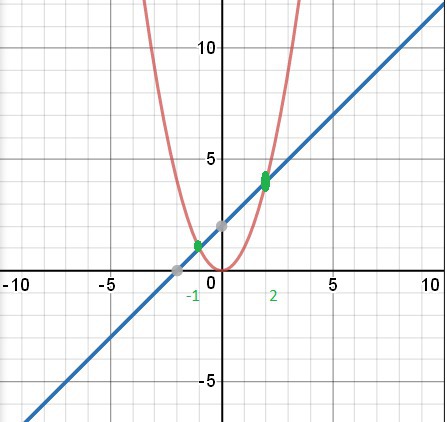
  • 1) Постройте в одной и той же системе координат графики функций y=x и y=x+2. Найдите с помощью графиков функций координаты точек пересечения этих графиков.
    2) Найдите координаты точек пересечения графиков функций, данных в 1 задаче, решая систему уравнений. При этом для нахождения корней многочлена разложите уравнения на множители.


    Решение: Х²=х+2
    х²-1=х+1
    (х-1)(х+1)=х+1
    (х-1)(х+1)-(х+1)=0
    (х+1)(х-1-1)=0
    (х+1)(х-2)=0
    х+1=0  или  х-2=0
    х=-1  или  х=2
    Второй способ:
    х²-х-2=0
    D=(-1)²-4·(-2)=9
    x=(1-3)/2=-1  или   х=(1+3)/2=2
    Графическое решение см. рисунок.
    О т в е т.1; 2

    Х х х - х х- х х х- х - х х х- - х х- х   или  х- х -   или  х Второй способ х -х- D - - - x - -   или   х Графическое решение см. рисунок.О т в е т....

  • Найти координаты точек пересечения графиков функций: у=6+х и у=х^2-4х. И уравнение. 16х^4 + 4х^2 - 2 = 0


    Решение: 16х4+4х2-2=0

    данное уравнение-биквадратное

    х2=т

    16т2+4т-2=0 делим все на 1

    8т2+2т-1=о

    Д=4+32=36

    х1=-2- 6 делить на 16=-18/16=-6/8=-3/4

     х2=-2+6/18=4/18=2/9

    итак возвращаемся

    2 /9

    минус, плюс корень из 2 делить на 3 

    составим систему :

    y=6+x

    y=x²-4x

    первое уравнение, можно подставить во второе:

    6+х=х²-4х

    -x²+5x+6=0

    x²-5x-6=0

    D=25+24=49

    D=7

    x=(5+7)/2=6

    x2=5-7/2=-1

    y1=6+6=12                    y=6²-4*6=36-24=12

    y2=6-1=5                      y2 = 1+4=5

    ответ: (6;12)(-1;5)

  • Линейная функция задана формулой y=2x+3. Найдите значение функции, если значение аргумента равно 0.
    Линейная функция задана формулой y=3х-5. Найдите значение функции, если значение функции равно 1.
    Не выполняя построения графиков, укажите координаты точек пересечения графиков
    у=16х+15.
    Не выполняя построений, найдите координаты точек пересечения графика функции
    у= -2х+2 с осями координат.


    Решение: 1) y=2x+3
      x=0 y=2*0+3=3
    Ответ: 3
    2) у=3х-5
    х=1 у=3*1-5= -2
    Ответ: -2
    3) у=16х+15
    с осью ОХ: у=0 0=16х+5
      -5=16х
      х= -5/16
    (-5/16; 0) - точка пересечения графика с осью ОХ.
    с осью ОУ: х=0 у=16*0+5
      у=5
    (0; 5) - точка пересечения графика с осью ОУ.
    4) у= -2х+2
    с осью ОХ: у=0 0= -2х+2
      -2= -2х
      х=1
    (1; 0) - точка пересечения графика с осью ОХ.
    с осью ОУ: х=0 у= -2*0+2
      у=2
    (0; 2) - точка пересечения графика с осью ОУ.

  • 1. Составьте формулу квадратичной функции, если вершина параболы находится в точке А(-5,1,5) и а=1 2. Составьте формулу квадратичной функции, если а=-1, координаты вершины параболы х=-3 и у=2 3. Найдите абсциссы точек пересечения графика функции у=х²+2,5х-1,5 с осью Ох 4. Найдите координаты точек пересечения графика функции у=-х²+2х-3 с осью ординат 5. Найдите координаты точек пересечения графиков функций у=х²-2х и у=-х²+2х


    Решение: 1) общая формула квадратичной функции y=ax^2+bx+c

    найдем b: 

    x0=-b/2a=-5

    -b/2=-5

    b=10

    найдем c:

    -1,5=(-5)^2+(-5)*10+c

    c=-1,5-25+50=23,5

    получается функция y=x^2-5x+23,5

    2)

    проделываем всё тоже самое.

    -b/2a=-3

    -b/-2=-3

    b/2=-3

    b=-6

    2=(-1)*(-3)^2-6*(-3)+c

    c=2+9-18

    c=-7

    получаем функцию y=-x^2-6x-7 

  • Постройте график функции и найдите координаты точек пересечения графиков y=2x-2 и y=-4


    Решение: 1)y=2x-2 - линейная функция, графиком является прямая, проходящая через точку (0;-2)
    если х=0, то у=-2, если х=1, то у=0
    у=-4 - линейная функция, графиком является прямая, проходящая через точку (0;-4)
    если х=0, то у=-4, если х=1, то у=-4.
    Строим координатную плоскость и на ней графики
    Точка пересечения - х=-1, у=-4.
    Если не трудно, сделай лучший ответ, чтобы мне дальше звания получать)))

  • Найти координаты точек пересечения графиков:
    a)y=2/5x и y=0.4x-1
    б)y=4.2x+2 и y=-4.2x-2
    в)y=3x+1 и y=x+1
    г)y=2x+5 и y=2x-10
    д)y=37x-8 и y=25x+4


    Решение: Линейная функция 
    а)K1=2/5 K2=0.4 значит есть только одна точка пересечения 
    Теперь нужно составить уравнение 2/5х=0,4х-1
    2/5х-0,4х=-1
    и так найдите х.
    потом к любой из двух  функций напишите значение х и найдите у 
    б) нет точки пересечения т. к К1=К2 
    в) нет точки пересечения т. к К1=К2 
    г) нет точки пересечения т. к К1=К2 
    д) посмотри А и реши 

  • Найдите координаты точек пересечения графиков функций y-x2+6x-4 и y=24/x


    Решение: Для этого нужно решить систему двух уравнений:
    $$ \left \{ {y= x^{2} +6x-4} \atop {y=\frac{24}{x}} \right. $$
    Приравниваем правые части уравнений
    $$ x^{2} +6x-4= \frac{24}{x}, \\ x^{3}+6 x^{2} -4x-24=0,x = 0 $$
    Разложим на множители способом группировки:
    х²(х+6)-4(х+6)=0,
    (х+6)(х²-4)=0
    х+6=0  или  х²-4=0
    х=-6  или  х=2  или  х=-2
    у=$$ \frac{24}{(-6)}=-4 $$  у= 12  у=-12
    Ответ. (-6;-4)  (2; 12)  (-2; -12)

  • Найдите координаты точек пересечения графиков функций, затем проверьте их, построив графики функций:y=0,5x+4 и y=2x+4


    Решение: 0,5X + 4 = 2X + 4 
    2X - 0,5X = 4 - 4 
    0,5X = 0
    X = 0
    -
    Y = 2X + 4 
    Y = 4 
    -
    Точка пересечения данных графиков имеет координаты ( 0 ; 4)
    -
    Построение графиков:
    1) Y = 0,5X + 4 ( прямая линия)
    Отмечаем точку А ( 0 ; 4 ) и точку B ( 2 ; 5 ) Cоединяем точки А и В ( это и есть график функции Y = 0,5X + 4 )
    2) Y = 2X + 4 ( прямая линия ) 
    Отмечаем точку С ( 0 ; 4 ) и точку D ( 1 ; 6 ) Cоединяем точки C и D ( это и есть 
    график функции Y = 2X + 4 
    -
    Данные два графика пересекутся в точке ( допустим Е ) с координатами 
    ( 0 ; 4 ), это и есть проверка правильности нашего решения
     

1 2 3 > >>