координаты »

определите координаты точек пересечения графиков - страница 3

  • Найдите координаты точек пересечения графиков функций y = х2(в квадрате) и y = 5х – 6 (графически)


    Решение: y1=x^2
    x=0,x=1, x=2, x=-1, x=-2y=0,
     y=1, y=4, y=1, y=4
    y2=5x-6x=0,
    x=1, x=2, x=-1, x=-2
    y=-6, y=-1, y=4, y=-11, y=-16
    точка пересечения этих прямых, точка "А" я ее обвела красным кругом.
    Ее координаты (2;4)
    Ответ: А(2;4)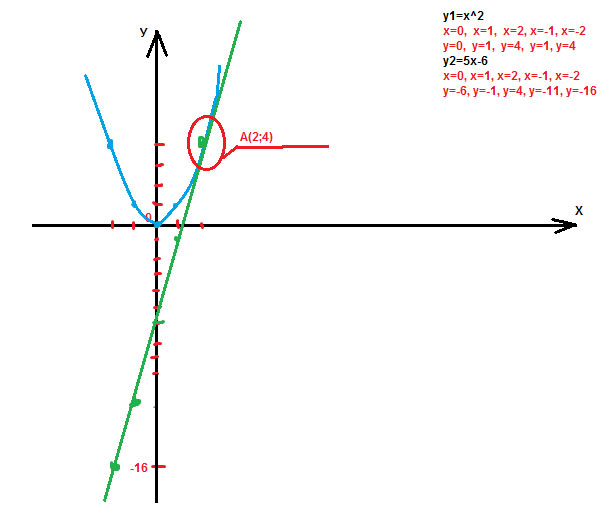

    y x x x x x - x - y  y y y y y x- x x x x - x - y - y - y y - y - точка пересечения этих прямых точка А я ее обвела красным кругом.Ее координаты Ответ А...

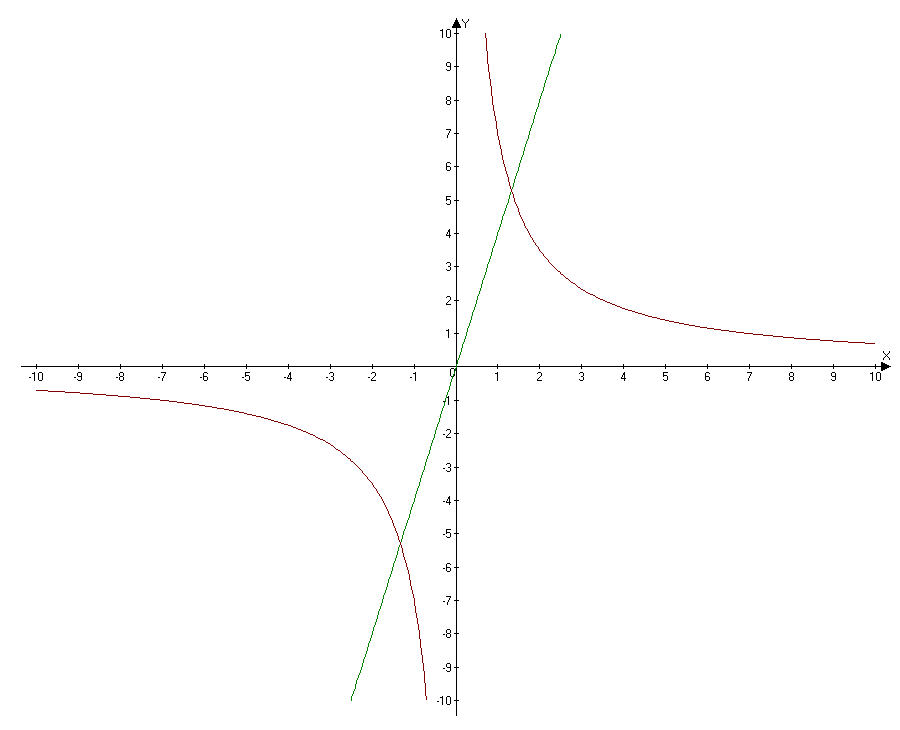
  • Найдите координаты точек пересечения графиков функций y=4x и y=7/(x+1)-1.


    Решение: У=4х
    у=7/х
    Для определения координат точек пересечения нужно приравнять правые части обоих уравнений найти значения "х" при которых выполняется равенство, затем найденные х подставить в одно из уравнений (удобнее по расчетам в первое) и найти значения у соответствующие этим значениям. 
    Полученные пары х и у и будут координатами точек пересечения.
    Предварительно можно сказать, что первый график - прямая, проходящая через начало координат, а второй гипербола находящаяся в первом и третьем квадрантах.
    4х=7/х,   4х^2=7,    x 1,2 = +- √7 /2,   x1=√7 /2,    x2= -√7 /2
    y=4x
    y1=4*x1=2√7
    y2=4*x2= -2√7
    Т. о. координаты точек пересечения графиков:
    х1= √7 /2    у1=2√7
    х2= -√7 /2    у2= -2√7

    У ху хДля определения координат точек пересечения нужно приравнять правые части обоих уравнений найти значения х при которых выполняется равенство затем найденные х подставит...

  • Найдите координаты точек пересечения графиков функции y=x^2 + 8x + 15 c осью ОХ


    Решение: Ось ОХ задаётся функцией y=0, по этому, чтобы найти точки пересечения с осью ОХ, нужно приравнять эти функции:
    y = 0
    y = x² + 8x + 15
    x² + 8x + 15 = 0
    Обычное квадратное уравнение, решается через дискриминант:
    $$ D=64-60=4 \\\\\sqrt{D}=2 \\\\x_1=\frac{-8+2}{2}=-3\\\\x_2=\frac{-8-2}{2}=-5 $$
    Ответ: точки пересечения: x = -3 ; x = -5.

  • Найдите координаты точек пересечения графиков функций
    y= x^3\х-2 и y=x^2-3x+1.
    Найдите координаты точек пересечения графиков функций
    y=x/x-3 и y=3x-4/2x


    Решение: 1) Найти координаты точек пересечения графиков функций 
      y= x³/(х-2) и y=x²-3x+1.
      Приравниваем  x³/(х-2) = x²-3x+1.
      х³ = х³-2х²-3х²+6х+х-2.
      Получаем квадратное уравнение:
      5х²-7х+2 = 0.
      Квадратное уравнение, решаем относительно x:   Ищем дискриминант:
      D=(-7)^2-4*5*2=49-4*5*2=49-20*2=49-40=9;  Дискриминант больше 0, уравнение имеет 2 корня:
      x₁=(√9-(-7))/(2*5)=(3-(-7))/(2*5)=(3+7)/(2*5)=10/(2*5)=10/10=1;
      у₁ = 1/(1-2) = -1.  x₂=(-√9-(-7))/(2*5)=(-3-(-7))/(2*5)=(-3+7)/(2*5)=4/(2*5)=4/10=0,4.
      у₂ = 0.064/(0,4-2) = -0,04.
      Имеем 2 точки пересечения:
      (1; -1) и (0,4; -0,04).
    2) Найти координаты точек пересечения графиков функций   y=x/(x-3) и y=(3x-4)/2x.
      Приравниваем x/(x-3) = (3x-4)/2x.
      2х² = 3х²-4х-9х+12,
      Получаем квадратное уравнение:
      х²-13х+12 = 0.
      Квадратное уравнение, решаем относительно x:   Ищем дискриминант:
      D=(-13)^2-4*1*12=169-4*12=169-48=121;  Дискриминант больше 0, уравнение имеет 2 корня:
      x₁ = (√121-(-13))/(2*1)=(11-(-13))/2=(11+13)/2=24/2=12;
      у₁ = 12/(12-3) = 12/9 = 4/3.  x₂=(-√121-(-13))/(2*1)=(-11-(-13))/2=(-11+13)/2=2/2=1.
      у₂ = 1/(1-3) = -1/2.
      Имеем 2 точки пересечения: (12; (4/3)) и (1; (-1/2)).

  • Найдите координаты точек пересечения графиков функций у=х³/х-2 и у=х²-3х+1


    Решение: Х³/(х-2)=х²-3х+1
    х³=(х-2)*(х²-3х+1)
    х³=х³-3х²+х-2х²+6х-2
    х³=х³-5х²+7х-2
    5х²-7х+2=0
    D=49-40=9 √D=3
    х₁=(7+3)/10=1 у₁=1³/(1-2)=-1
    х₂=(7-3)/10=0.4 у₂=(0.4)³/(0.4-2)=0.064/(-1,6)=-0.04
    Ответ: ( 1; -1),( 0,4 ; -0.04)

    $$ \frac{x^3}{x-2}=x^2-3x+1 \\ x^3=(x^2-3x+1)(x-2) \\ x^3=x^3-3x^2+x-2x^2+6x-2=0 \\ x^3-x^3-3x^2-2x^2+6x+x-2=0 \\ -5x^2+7x-2=0 \\ D=b^2-4ac=7^2-4*(-5)*(-2)=49-40=9 \\ x_1= \frac{-7+ \sqrt{9} }{2*(-5)}= \frac{-7+3}{-10}=0.4 \\ \\ x_2= \frac{-7- \sqrt{9} }{2*(-5)}= \frac{-7-3}{-10}=1 $$
    точками пересечения графиков будут
    $$ f(0.4)= \frac{0.4^3}{0.4-2}= \frac{0.064}{-1.6} =-0.04 $$
    первая точка (0,4;-0,04)
    $$ f(1)= \frac{1^3}{1-2}= \frac{1}{-1}=-1 $$
    вторая точка (1;-1)

<< < 123 4 5 > >>