координаты »

определите координаты точек пересечения графиков - страница 4

  • Найдите координаты точек пересечения графиков функций \( y=\frac{x^3}{x-2}\) и \(y=x^2-3x+1\)


    Решение: $$ y= \frac{x^3}{x-2} \\ y=x^2-3x+1 \\ \frac{x^3}{x-2}=x^2-3x+1 \\ x-2 = 0 \\ x = 2 \\ x^3=(x^2-3x+1)(x-2) \\ x^3=x^3-3 x^{2} +x-2 x^{2} +6x-2 \\ x^3-3 x^{2} +x-2 x^{2} +6x-2-x^3=0 \\ -5 x^{2} +7x-2=0 \\ 5 x^{2} -7x+2=0 \\ D=(-7)^2-4*5*2=9 \\ x_1= \frac{7+3}{10} =1 $$, $$ y_1= \frac{1}{1-2} =-1 \\ x_2= \frac{7-3}{10} =0.4 $$, $$ y_2= \frac{0.064}{0.4-2} =-0.04 $$
    Ответ: (1;-1) и (0.4; -0.04)

    Для нахождения точек пересечения графиков функций нам нужно отыскать такие значения аргумента при которых значений функций будут равны

  • Найдите координаты точек пересечения графиков функций:
    y=\( \frac{2}{x} \) и y=x+1


    Решение: 2/x=x+1
    x^2+x=2, причем х не равен 0
    x^2+x-2=0
    По Виета:
    х1=-2
    х2=1
    у1=-2+1=-1
    у2=1+1=2
    Ответ: (-2;-1) и (1;2)x x x x причем х не равен x x- По Виета х - х у - - у Ответ - - и...

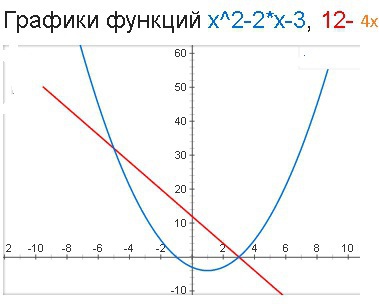
  • Найдите координаты точек пересечения графиков функций y=x^2-2x-3 и y=12-4x


    Решение: Приравняем оба выражения и найдем корни уравнения
    x²-2x-3=12-4x
    x²+2x-15=0
    x1-2=(-2+-√(4+60))/2=(-2+-8)/2
    x1=(-2+8)/2 =3
    x2=(-2-8)/2=-5
    подставив значения х в любое из выражений, например во второе,
     найдем у
     x=3, y=12-4x=12-12=0 первая точка (3;0)
    x=-5, y=12-4x= 12+20=32 вторая точка (-5;32)

    Приравняем оба выражения и найдем корни уравненияx - x- - xx x- x - - - - - x - x - - - подставив значения х в любое из выражений например во второе  найдем у x y - x - перва...

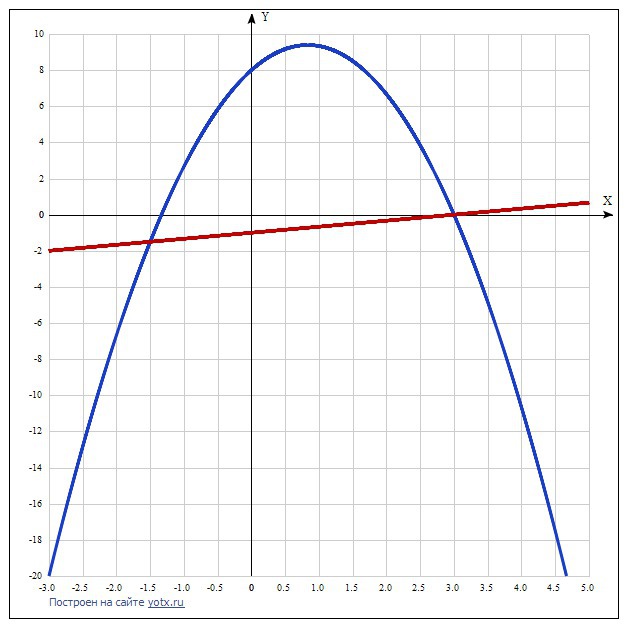
  • Найдите координаты точек пересечения графиков функции: y=x/3 - 1 и y=-2(x-3) * ( x +1( 1/3)


    Решение: Уравнение y=-2(x-3) * ( x +1( 1/3) преобразуем, раскрыв скобки:
    у = -2х² + (10/3) х + 8.
    Для определения точек пересечения графиков функции: y=x/3 - 1 и y=-2(x-3) * ( x +1( 1/3) надо их приравнять - общие точки принадлежат обоим графикам:
    -2х² + (10/3) х + 8 = (1/3) х -
    -2х² + (9/3) х + 9 = 0,
    -2х² + 3х + 9 = 0.
    Квадратное уравнение, решаем относительно x: 
    Ищем дискриминант:D=3^2-4*(-2)*9=9-4*(-2)*9=9-(-4*2)*9=9-(-8)*9=9-(-8*9)=9-(-72)=9+72=81;
    Дискриминант больше 0, уравнение имеет 2 корня:x_1=(√t81-3)/(2*(-2))=(9-3)/(2*(-2))=6/(2*(-2))=6/(-2*2)=6/(-4)=-6/4=-1.5;
    x_2=(-√81-3)/(2*(-2))=(-9-3)/(2*(-2))=-12/(2*(-2))=-12/(-2*2)=-12/(-4)=-(-12/4)=-(-3)=3.
    Ответ: х_1 = -1,5, у = (1/3)*(-3/2) - 1 = -1,5,
      х_2 = 3, у = (1/3)*3 - 1 = 0.

    Уравнение y - x- x преобразуем раскрыв скобки у - х х    .Для определения точек пересечения графиков функции y x - и y - x- x надо их приравнять - общие точки принадлежат обо...

  • Найдите координаты точек пересечения графиков функций y=-4x+11 и y=12x+75


    Решение: Приравниваем, получаем -4x+11=12x+75 находим х, он равен-4 Теперь подставляем х в любую функцию у=-4*-4+11 у= 27 пересечение (-4;27)

    Приравнять: -4х+11=12х+75
    -16х=64
    х=64/(-16)
    x=-4
    затем подставить х в любое из этих ур-ний
    у=-4(-4)+11
    у=27
    можно ещё проверку сделать:
    27=12(-4)+75
    27=-48+75
    27=27
    т. е. точки пересечения(-4;27)

<< < 234 5 6 > >>