на координатной прямой найдите координату точки
Решите неравенство и покажите на координатной прямой множество его решений
|x| < 3
|у| ≥ 5
Решение: 1)
х<3 и -х<3
х >-3
_____-3//////////////////////3________ точки -3 и 3 выколотые (-3;3)
2)
у≥5 и -у ≥5
у≤-5
//////////////-5______________5///////////////// Точки -5 и 5 закрашенные
(-∞;-5] ∪[5;+∞)]Решите неравенство и покажите на координатной прямой множество его решений: /x/<3, /x/< или равно 4, /y/> или равно 5,/y/>2.
Решение: |x|<=4-нет решения
|y|>2
------------------->
-2 -1 0 1 2
Ответ: (-∞; 2)|x|<3 ⇔ -3<x<3, на координатной прямой - это числа от -3 до 3 (сами числа -3 и 3 не считаются)
|x|≤4 ⇔ -4≤x≤4, на коорд. прямой - это числа от -4 до 4 (числа -4 и 4 входят)
|y|≥5 ⇔ y≤-5 и y≥5, на коорд. прямой - это числа, левее -5 (-5 входит) и числа, правее 5 (5 входит)
|y|>2 ⇔ y<-2 и y>2, на коорд. прямой - это числа, левее -2 и правее 2.Решите неравенство и покажите на координатной прямой множество его решений: [x]<3, [х]< или равно 4, [y]> или равно 5,[y]>2
Решение: [x] - это целая часть числа? Если да, то решение: x ∈ [0; 3)
А если это модуль, то решение: x ∈ (-3; 3)
[x] <= 4. Опять-таки, для целой части решение x ∈ [0; 4]
Для модуля решение x ∈ [-4; 4]
[y] >= 5. Тут решения [5; +oo) или (-oo; -5] U [5; +oo)
[y] > 2. Тут решения (2; +oo) или (-oo; -2) U (2; +oo)X^2 - 2х - 3 <= 0 (Меньше либо равно)
Решить неравенство и показать на координатной прямой
Решение: X^2-2x-3<=0
Приравниваем к нулю и решаем уравнение:
x^2-2x-3=0
D=4+4*3=16
√16=4
x₁=(2+4)/2=6/2=3
x₂=(2-4)/2=-2/2=-1
отмечаем точки на координатной прямой
___________+__________-1________-___________3_____+_____>
x∈[-1;3]
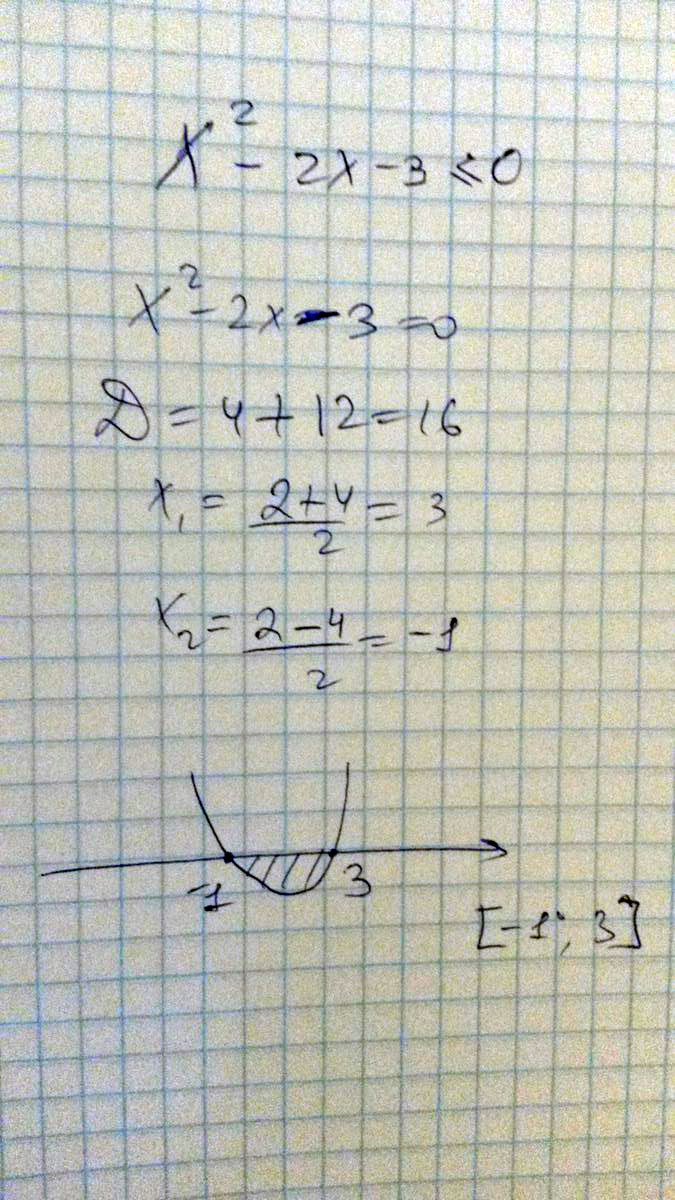
Решите неравенство и изобразите его решение на координатной прямой:
1) 4, 5х - 1, 4 =7,6;
2) 3х-1,2 3, 3;
3) 7-1,2 > 2+3,8х;
4) 3х+7 < х-1.
Решение: 4.5х-1,4=7,6тогда 4,5х = 9 отсюда х=2. и на координатной плоскости отметь 2. Если больше там было то будет (2; до + бесконечности) если там знак меньше. то (- беск до 2)
3х=4,5
х= 1,5 и то же самое.
3) 7-1,2>2+3,8x
7 - 1,2 - 2>3,8x
3,8>3,8x
x<1 также чертите. Ответ (от - бесконечности до1)
4) 3x + 7 < x-1
2x < -8
x<-4
все так же чертите. Ответ (-4; + беск)

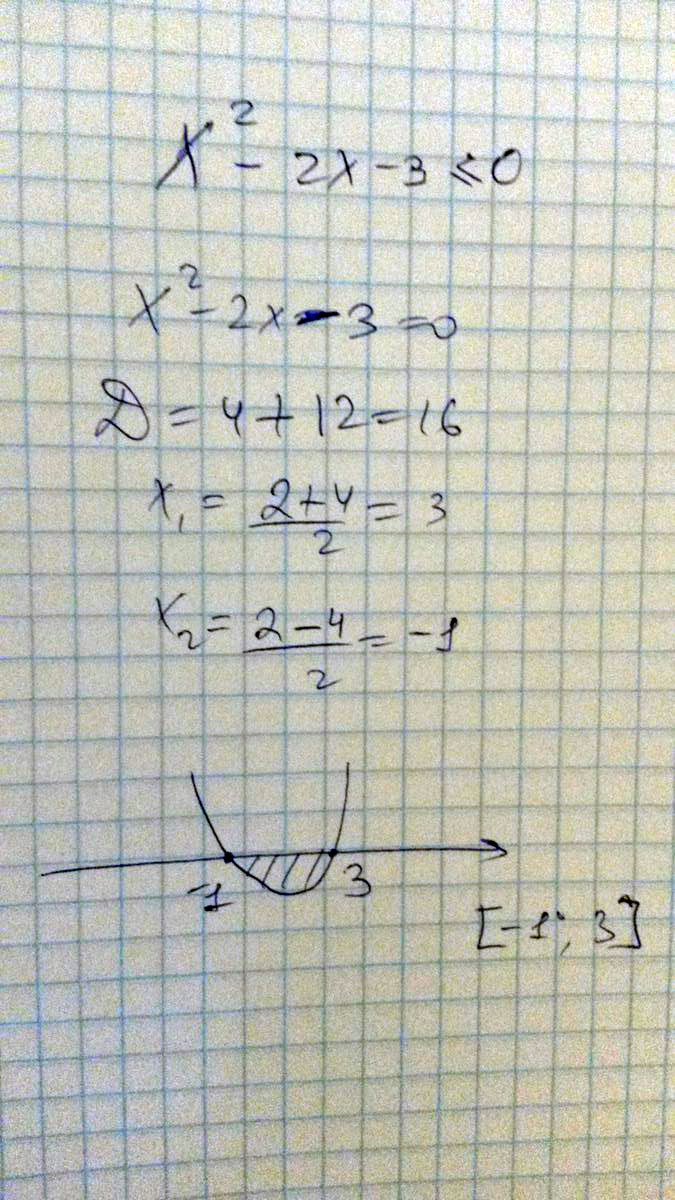
 Декартова система координат
Пусть в пространстве заданы две различные произвольные точки О и М, и пусть одна из них, например точка О, выбрана в качестве начальной. Тогда вектор \(\vec{OM}\) называется радиус-вектором точки М относительно точки О (рис.).
Пусть в пространстве задана точка О и некоторый базис e1, e2 , e3. Совокупность этого базиса и точки О называется декартовой системой координат О,...
Декартова система координат
Пусть в пространстве заданы две различные произвольные точки О и М, и пусть одна из них, например точка О, выбрана в качестве начальной. Тогда вектор \(\vec{OM}\) называется радиус-вектором точки М относительно точки О (рис.).
Пусть в пространстве задана точка О и некоторый базис e1, e2 , e3. Совокупность этого базиса и точки О называется декартовой системой координат О,... Выбором прямоугольной декартовой системы координат устанавливается взаимно однозначное соответствие между точками плоскости и упорядоченными парами действительных чисел. Это означает, что каждой точке плоскости соответствует единственная пара чисел и каждой упорядоченной паре действительных чисел соответствует единственная точка.
Выбор той или иной системы координат ничем не ограничен и определяется в каждом конкретном случае только соображениями удобства. Часто одно и то же множество приходится...
Выбором прямоугольной декартовой системы координат устанавливается взаимно однозначное соответствие между точками плоскости и упорядоченными парами действительных чисел. Это означает, что каждой точке плоскости соответствует единственная пара чисел и каждой упорядоченной паре действительных чисел соответствует единственная точка.
Выбор той или иной системы координат ничем не ограничен и определяется в каждом конкретном случае только соображениями удобства. Часто одно и то же множество приходится...