координаты »

на координатной прямой найдите координату точки - страница 4

  • укажите сделайте рисунок где на координатной прямой расположены числа модули которых равны 3 ; меньше 3; больше 3


    Решение: ...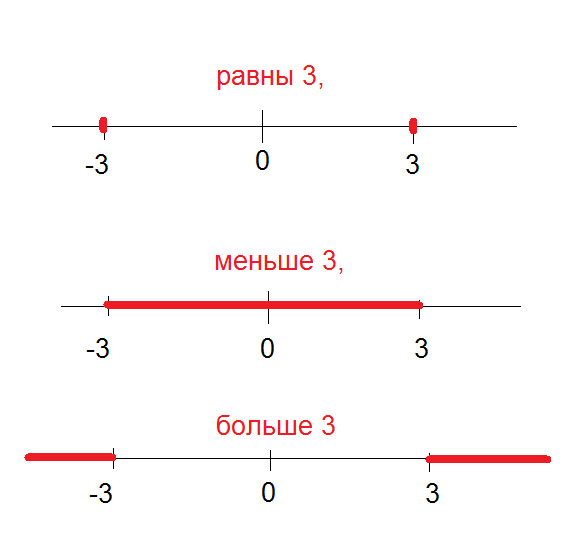

  • 1. Заданы числа с координатами. Укажите их на координатной прямой:
    A(2); B(9,1); C(0); D(-1); E( -4(2⁄9);
    2. Найдите числа, противоположные заданным числам:
    -30; 0,45; - 4 3⁄8; 2,9; -3 3⁄14 ;
    3. Найдите модуль чисел: 12; -6; 9; -52⁄7
    4. Вычислите:
    | 3,6 | * | - 8 | - | 2 5 ⁄7 | * | - 2⁄5 |
    5. Заданы числа. Сравните их и результат запишите в виде неравенства:
    а) 2⁄3 и 5⁄7
    б)- 3 4⁄9 и - 3 5⁄9


    Решение: 1.4 2/9  -1  0  2 9,1  ________E________D____C_______A______________B_________
    2.30*(-1)=30  0,45*(-1)=-0,45
       -4 3/8=4 3/8 ; 2,9*(-1)=-2,9  -3 3/14*(-1)=3 3/14
    3. |12|=12 ; |-6|=6  ;  |9|=9; |-52/7|=52/7
    4. |3,6|*|-8|-|2 5/7|*|-2/5|=3,6*8-19/7*2/5=28,8-38/35=970/35=194/7=27 5/7
    5. 2/3-5/7=(14-15)/21=-1/21<0 2/3<5/7
    -3 4/9-(-3 5/9)=1/9  >0  -3 4/9> -3 5/9

  • На оси координат найдите точку M, расстояние от которой до точки,A( 4;3;0) равно 5


    Решение: Точка М расположена на оси ординат, значит имеет координату по ОY какое-то число, а по осям ОХ и ОZ нулевые координаты: М(0; y; о)
    Расстояние МА=√((4-0)^2+(3-у)^2+(0-0)^2)=√(4^2+(3^2-6y+y^2)+0)=
    =√(16+9-6y+y^2)=√(y^2-6y+25)
    МА=5⇒√(y^2-6y+25)=5;
    y^2-6y+25=5^2;
    y^2-6y+25=25;
    y^2-6y=0;
    y(y-6)=0; ⇒y1=0;⇒М(0;0;0)
      ⇒y2=6⇒М(0; 6; 0)

<< < 234