найти координаты точек - страница 6
Не выполняя построений, найти координаты точек пересечения окружности x^2+y^2=1 и прямой 2y-x=5
Решение: 2y-x=5⇒x=2y-5
x²+y²=1
(2y-5)²+y²=1
4y²-20y+25+y²-1=0
5y²-20y+26=0
D=400-520=-120<0
нет решения⇒точек пересечения нетРешение .
2y-x=5
x=2y-5
x^2+y^2=1
(2y-5)^2+y^2=1
4y^2-20y+25+y^2-1=0
5y^2-20y+26=0
D=400-520=-120<0
Точек пересечения нет.x^2-9x+y^2+8y-20=0 найти координаты точек пересечения окружности с осью ординат.
Решение: Окружность пересекается с осью ординат в точке, координаты которой (0; у)подставляем её координаты в уравнение окружности:
0^2-9*0+у^2 + 8у-20=0
у^2+8у-20=0
D=8*8-4*(-20)*1=64+80=144=12^2
у1=(-8+12)/2=2
у2=(-8-12)/2=-10
Итак, данная окружность пересекается с осью ординат в двух точках с координатами (0;2) и (0;-10)
Прямая у=х пересекает параболу у=х2+3х-3. Найти координаты точек пересечения.
Решение: Если прямая прямая пересекает параболу, значит значения у будут равны. приравниваем:х=х^2+3x-3
x^2+2x-3=0
D=4+12=16
x1=1 x2=-3
но равны будут не только значения у, но и х.
получается, точки пересечения:
(1;1) (-3;-3)
а) Не выполняя построения, найти координаты точек пересечения параболы у = х ^ 2 (в квадрате) +4 и прямой х + у = 6
Решение: х²+4=6-хх²+4-6+х=0
х²+х-2=0
D= 1-4×1×(-2)=9
х₁=-2
х₂-1
у=6-х
у₁=6-(-2)
у₁=8
у₂=6-1
у₂=5
Значит (-2;8) и (1;5)
Solve for x over the real numbers:
x^2+4 = 6-x
Subtract 6-x from both sides:
x^2+x-2 = 0
The left hand side factors into a product with two terms:
(x-1) (x+2) = 0
Split into two equations:
x-1 = 0 or x+2 = 0
Add 1 to both sides:
x = 1 or x+2 = 0
Subtract 2 from both sides:
Answer: |
| x = 1 or x = -2Не выполняя построения, найти координаты точек пересечения параболы y=x2+4 и прямой x+y=6
Решение: 1) решаете систему.
2) подставляете во второе уравнение значение у.
3) потом через дискриминант находите.С помощью системы уравнений получаем линейное уравнение второй степени:
y2 - 13y + 40=0
через дискриминант находим корни.
y₁ = 16
y₂= 10
подставляем в уравнение:
х=y-6
x₁=16-6=10
x₂=10-6=4
Ответ: (10;16), (4;10)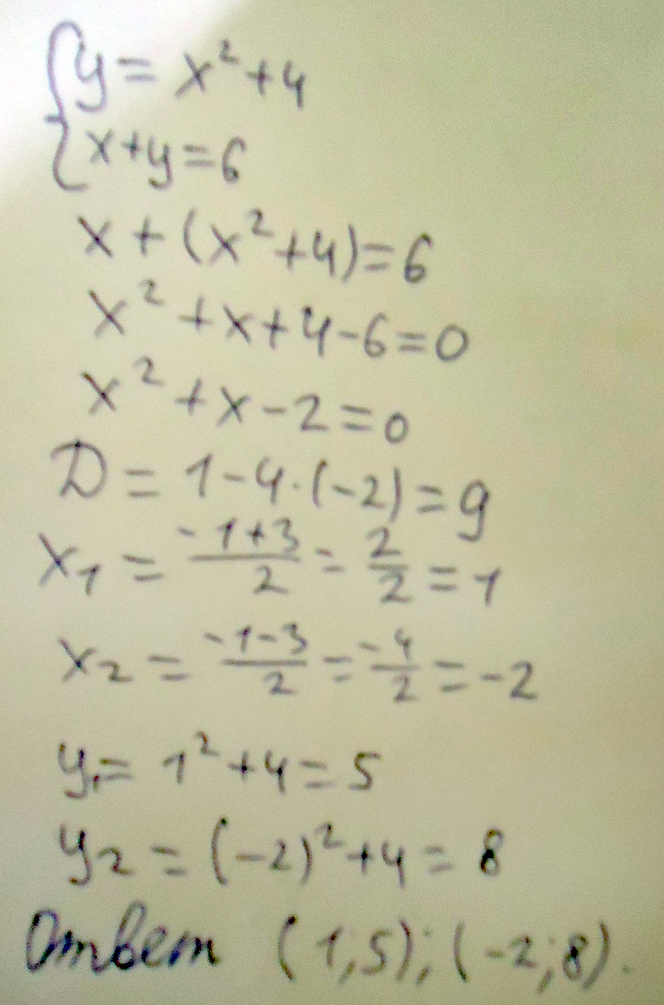

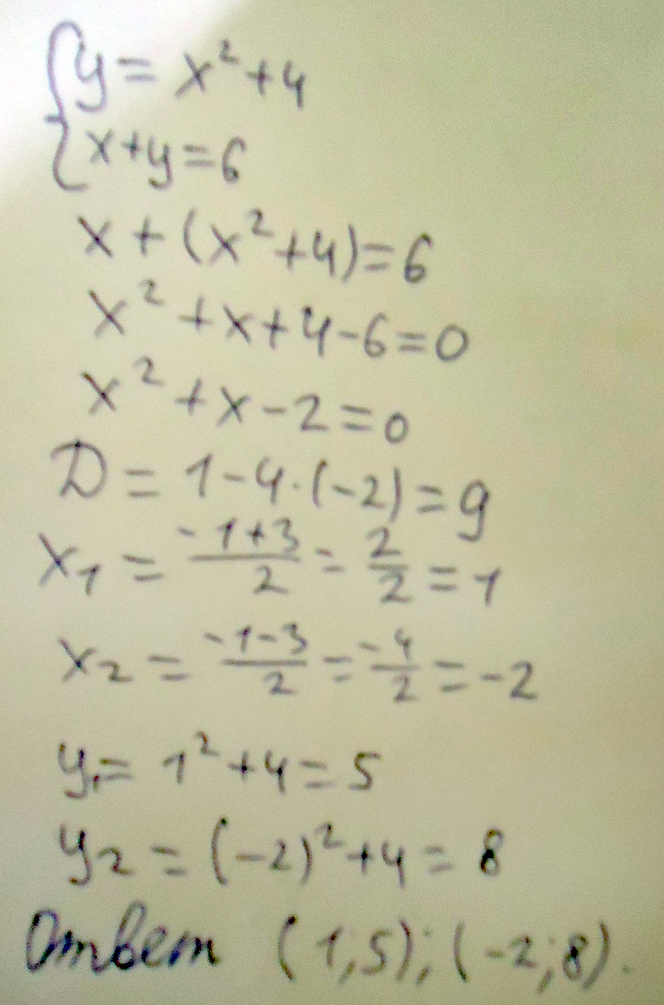
 Декартова система координат
Пусть в пространстве заданы две различные произвольные точки О и М, и пусть одна из них, например точка О, выбрана в качестве начальной. Тогда вектор \(\vec{OM}\) называется радиус-вектором точки М относительно точки О (рис.).
Пусть в пространстве задана точка О и некоторый базис e1, e2 , e3. Совокупность этого базиса и точки О называется декартовой системой координат О,...
Декартова система координат
Пусть в пространстве заданы две различные произвольные точки О и М, и пусть одна из них, например точка О, выбрана в качестве начальной. Тогда вектор \(\vec{OM}\) называется радиус-вектором точки М относительно точки О (рис.).
Пусть в пространстве задана точка О и некоторый базис e1, e2 , e3. Совокупность этого базиса и точки О называется декартовой системой координат О,... Выбором прямоугольной декартовой системы координат устанавливается взаимно однозначное соответствие между точками плоскости и упорядоченными парами действительных чисел. Это означает, что каждой точке плоскости соответствует единственная пара чисел и каждой упорядоченной паре действительных чисел соответствует единственная точка.
Выбор той или иной системы координат ничем не ограничен и определяется в каждом конкретном случае только соображениями удобства. Часто одно и то же множество приходится...
Выбором прямоугольной декартовой системы координат устанавливается взаимно однозначное соответствие между точками плоскости и упорядоченными парами действительных чисел. Это означает, что каждой точке плоскости соответствует единственная пара чисел и каждой упорядоченной паре действительных чисел соответствует единственная точка.
Выбор той или иной системы координат ничем не ограничен и определяется в каждом конкретном случае только соображениями удобства. Часто одно и то же множество приходится...