координаты »

постройте в системе координат графики

  • В одной системе координат постройте схематически графики функций y = x^5 -1 и 1/x-1. Запишите координаты их
    общих точек (если они существуют).


    Решение:

    $$ x^5-1=\frac1x-1\\ x^5=\frac1x\\ x^6=1\\ x_1=1,\;x_2=-1\\ y_1=0,\\ y_2=-2 $$
    $$ A(1;0),\\B(-1;-2) $$ - общие точки (точки пересечения графиков).
    Графики во вложении.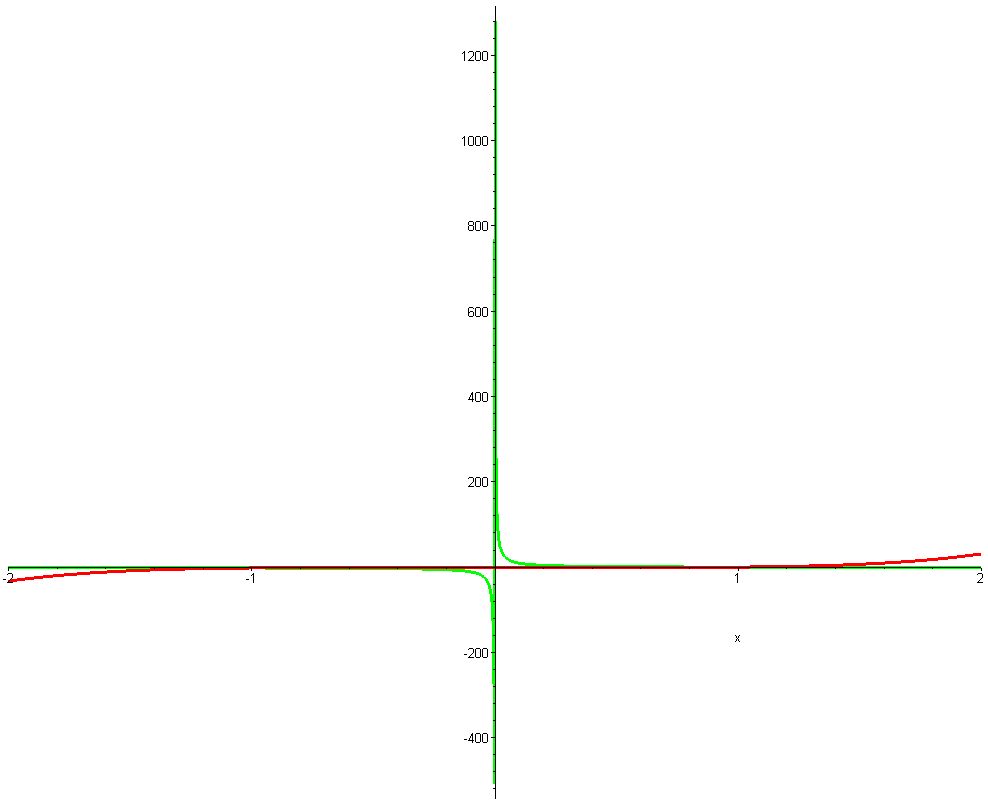 x - frac x- x frac x x x x - y y - A B - - - общие точки точки пересечения графиков .Графики во вложении....

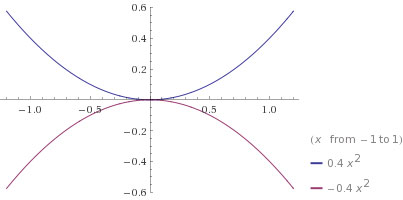
  • Постройте в одной системе координат графики функций y=0,4Х квадрат и y= -0,4х квадрат. Какова область значения каждой из этих функций?


    Решение: симметричные параболы

    y=0.4x^2 -ветви направлены ВВЕРХ

    область значения [0; +∞)

    y=-0.4x^2 -ветви направлены ВНИЗ

    область значения (-∞; 0]

    общая точка (0;0)

    симметричные параболы y . x -ветви направлены ВВЕРХ область значения y - . x -ветви направлены ВНИЗ область значения - общая точка...

  • Постройте в одной системе координат график функций у=-6х+9


    Решение: Y = -6x + 9

    Это график прямой, по скольку уравнение функции соответствует общей формуле прямой.
    y = kx + b
    В нашем случае k = -6 и b = 9.

    Для построения прямой нам достаточно взять две точки.
    Берём любые две цифры, подставляем вместо х и считаем сколько будет у.
    Например 1.
    y = -6*1 + 9 = 3
    И 2.
    y = -6*2 + 9 = -12 + 9 = -3
    Мы получили точки (1;3) и (2;-3).
    Проведём через них прямую.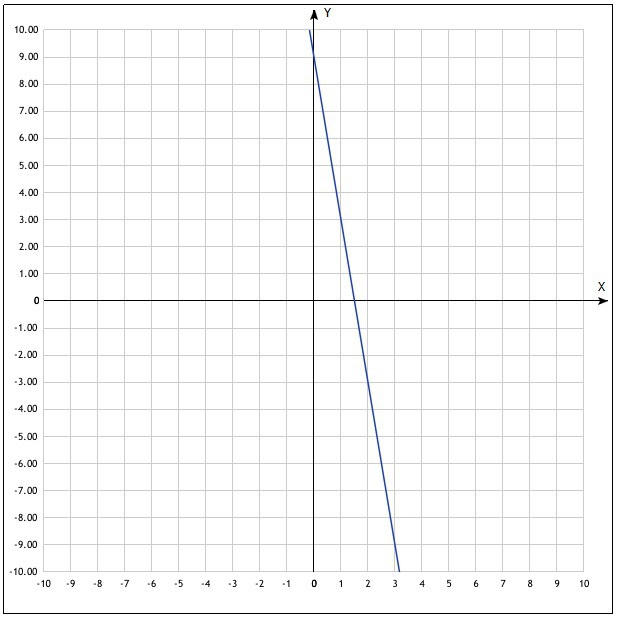
    Y - x Это график прямой по скольку уравнение функции соответствует общей формуле прямой. y kx bВ нашем случае k - и b .Для построения прямой нам достаточно взять две точки.Бер...

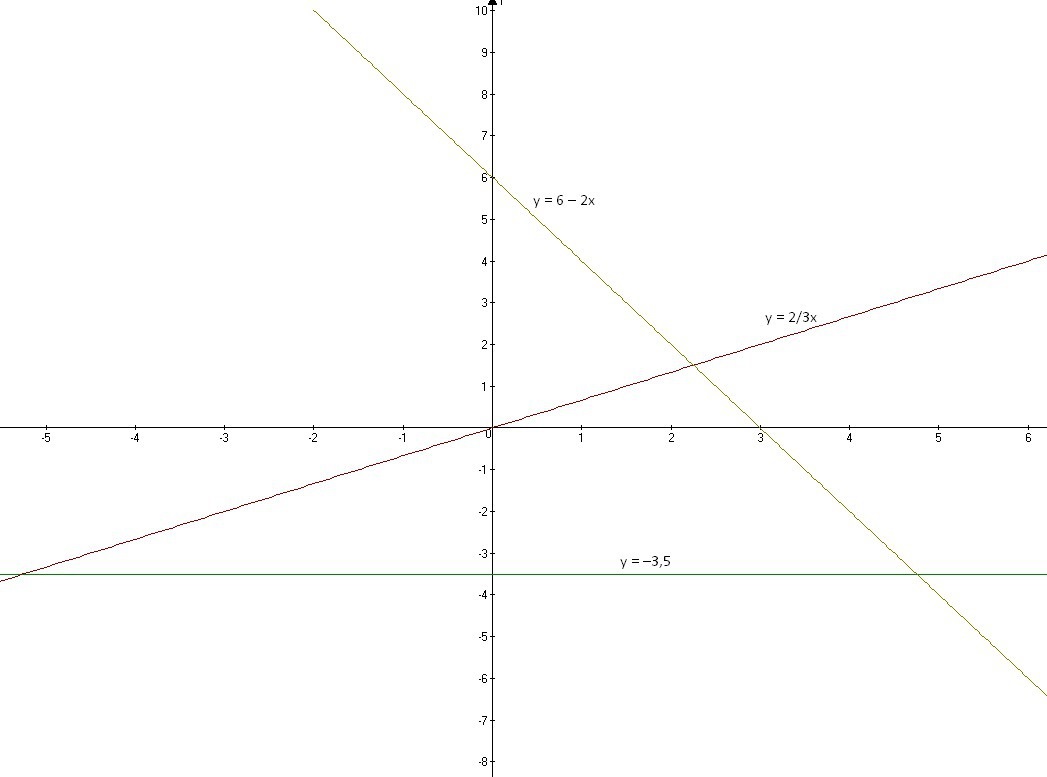
  • Постройте в одной системе координат графики функций y=-2x+6; y=2/3x y= -3.5


    Решение: 1–ая функция и её точки: 
    y=2(3-x)
    если x=3, то y=0
    если x=2, то y=2; 

    2–ая функция и её точки: 
    $$ y=\frac{2}{3}x $$
    если x=3, то y=2
    если y=6, то  y=4; 

    3–я функция и её точки: 
    y=-3,5
    Функция постоянна, поскольку нет зависимости от икса; игрек равен -3,5 в любой точке икс, а значит функция – постоянная прямая. 

    График во вложении. 
    ая функция и е точки   y -x если x то y если x то y   ая функция и е точки   y frac x если x то y если y то  y   я функция и е точки  y - Функция постоянна поскольку нет зави...

  • Постройте в одной системе координат графики функций y=x и y=-3x+3. Какая из этих функций является возрастающей?


    Решение: Построим графики предложенных функций на одной координатной плоскости. График функции $$ y = x $$ отметим красным цветом, а функции $$ y = -3x+3 $$ — синим. Из рисунка, прикрепленного к ответу, видим, что возрастает функция $$ y = x $$, так как она, грубо говоря, идет вверх.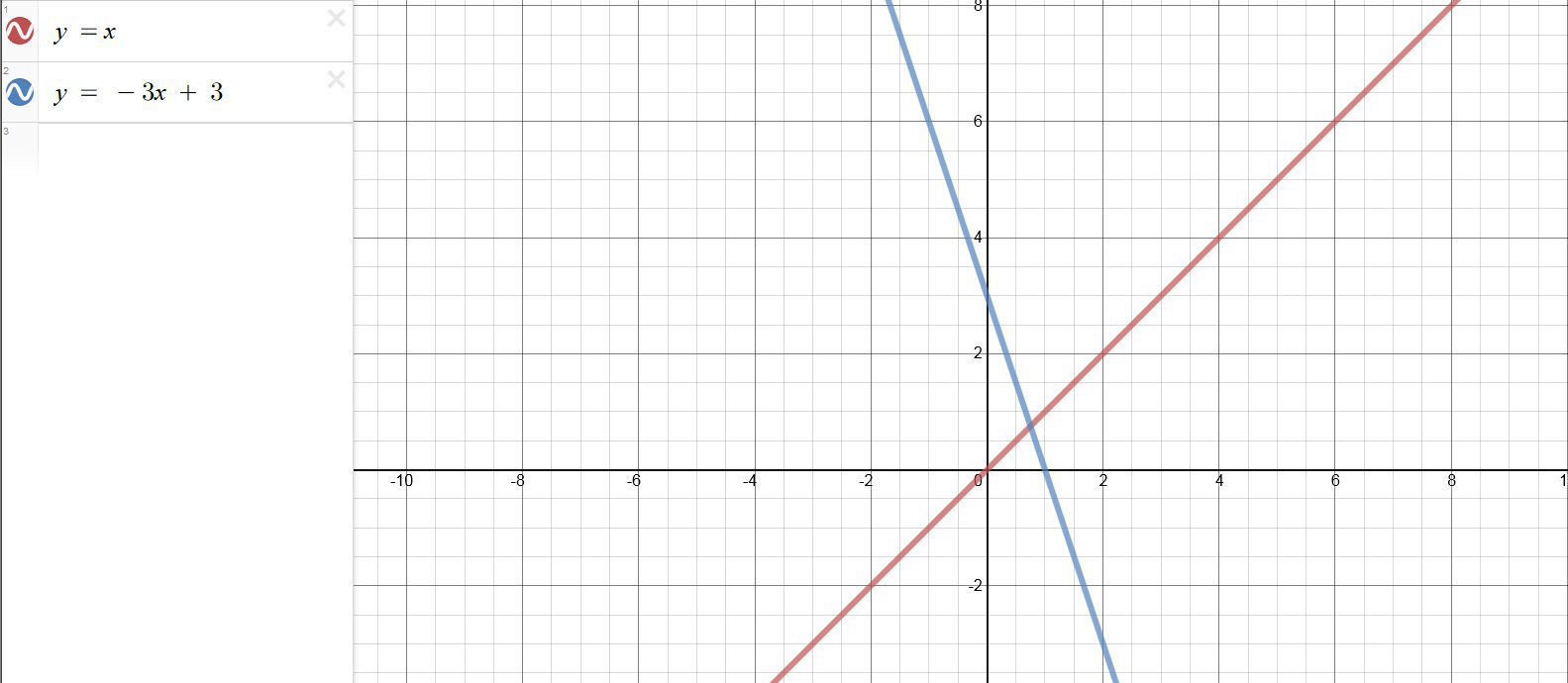  Построим графики предложенных функций на одной координатной плоскости. График функции y x отметим красным цветом а функции y - x синим. Из рисунка прикрепленного к ответу види...
1 2 3 > >>