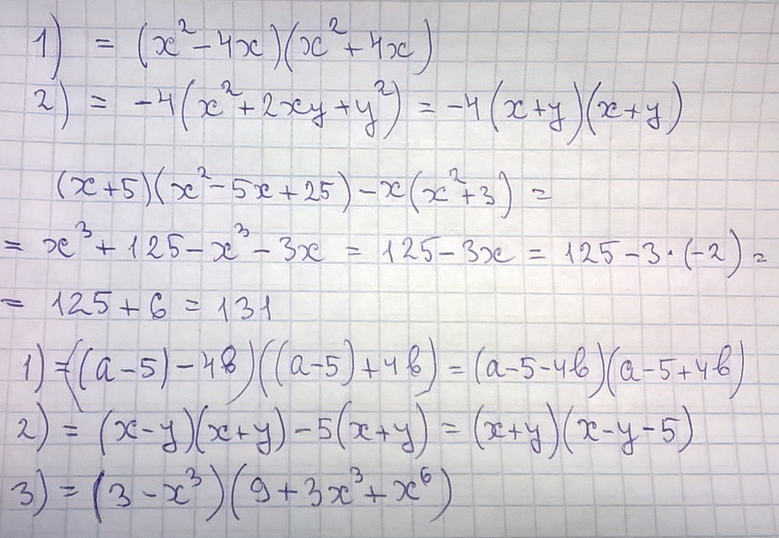представить многочлен в виде произведения - страница 2

Преобразования суммы и разности тригонометрических функций в произведение
1.) Напишите в виде произведения:
а) 1+2cosα
б) sin10+cos20
2.) Докажите тождество:
\( \frac{2cos^{2} \alpha -1 }{sin2 \alpha } + \frac{sin3 \alpha -sin \alpha }{cos3 \alpha +cos \alpha } = \frac{1}{sin2 \alpha } \)
3.) Напишите в виде произведения:
cosα-cosβ+sin(α+β)
4.) Упростите выражение:
\( \frac{1+tg \alpha }{1-tg \alpha } \)

Теорема Безу.
1. Выпишите строку коэффициентов многочлена:
x^2+5x^4-7x^3-2x^5.
2. Найдите значения многочлена непосредственной подстановкой и с помощью схемы Горнера:
3x^2+2x-4 при x=+-1,+-2,+-4.
3. Найдите целые корни многочлена:
5x^3-19x^2+11x+3;
4. Представьте в виде произведения многочленов:
5x^3+9x^2-5x-9;

1) Выполните умножение:
А) (x-8)(x+5)
Б)(3b-2)(4b-2)
В)(6а+x)(2а-3x)
Г)(с+1)(с+ 2 степень+3с+2)
2)
Разложите на множители:
А)2x(x-1)-3(x-1)
Б)ab+ac+4b+4с
3)
Представьте многочлен в виде произведения
kp-ks-px+cx+c-p
5) упростите выражение:
-0,4а(2а в квадрате)+3)(5-3а в квадрате)

Выполните умножение:

А) (x-8)(x+5)

Б)(3b-2)(4b-2)

В)(6а+x)(2а-3x)

Г)(с+1)(с+ 2 степень+3с+2)

2)

Разложите на множители:

А)2x(x-1)-3(x-1)=(x-1)(2x-3)

Б)ab+ac+4b+4с=(a(b+c)+4(b+c)=(b+c)(a+4)

3)

Представьте многочлен в виде произведения

kp-kc-px+cx+c-p=k(p-c)-x(p-c)-(p-c)=(p-c)=k-x-1)

5) упростите выражение:

-0,4а(2а^2+3)(5-3а^2)=-0.4a(10a^2-6a^4+15-9a^2)=-0.4a(a^2-6a^4+15)=-0.4a^3+2.4a^5-6a

Преобразовать в многочлен 2*(a-3)^2-2a^2
Разложите на множители
1) x^4-16x^2
2) -4x^2-8xy-4y^2
Упростите выражение и найдите его значение при x=-2
(x+5)*(x^2-5x+25)-x*(x^2+3)
Представьте в виде произведения:
1) (a-5)^2-16b^2
2) x^2-y^2-5x-5y
3) 27-x^9

2*(a-3)²-2a²=2(а²-6а+9)-2а²=2а²-12а+18-2а²=-12а+18
Разложите на множители
1) x^4-16x²=х²(х²-16)=х²(х-4)(х+4)
2) -4x²-8xy-4y²=-4(х²+2ху+у²)=-4(х+у)²
Упростите выражение и найдите его значение при x=-2
(x+5)*(x²-5x+25)-x*(x²+3)=х³+125-х³-3х=125-3·(-2)=125+6=131
Представьте в виде произведения:
1) (a-5)²-16b²=(а-5-4b)(a-5+4b)
2) x²-y²-5x-5y=(x-y)(x+y)-5(x+y)=(x+y)(x-y-5)
3) 27-x^9=3³-(x³)³=(3-x³)(9+3x³+x^60

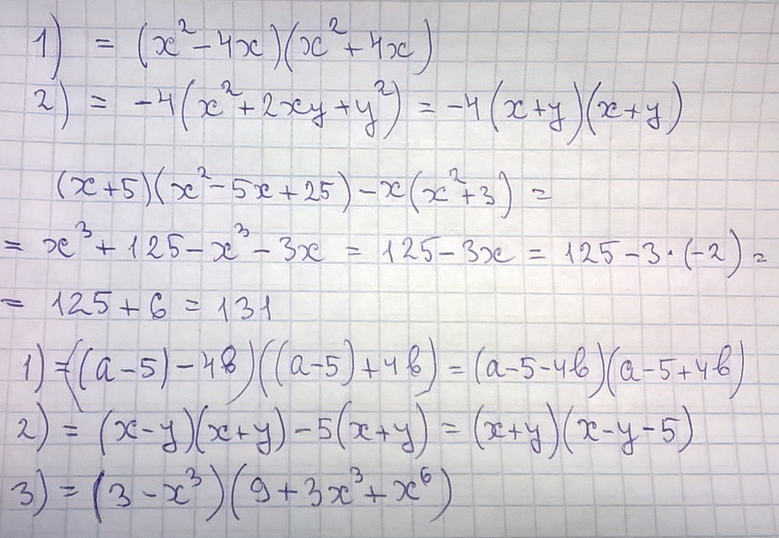
1. Сократите дробь:

16 - b2
b2 - b - 12
2. Разложите на множители квадратный трехчлен:
а) 2х2 - 5х +3;
б) 5у2 +2у - 3;
в) 3х2 - 24х + 21;
г) -2х2 +5х +7;
д) 3b2 +5b - 2;
е) -m2 +5m - 6.
3. Можно ли представить квадратный трехчлен в виде произведения многочленов первой степени:
а) х2 - 7х +12; б)
4b2 - 9b +7; в) 3у2 - 12у +12?
Если это возможно, то представьте квадратный трехчлен в виде произведения многочленов первой степени.