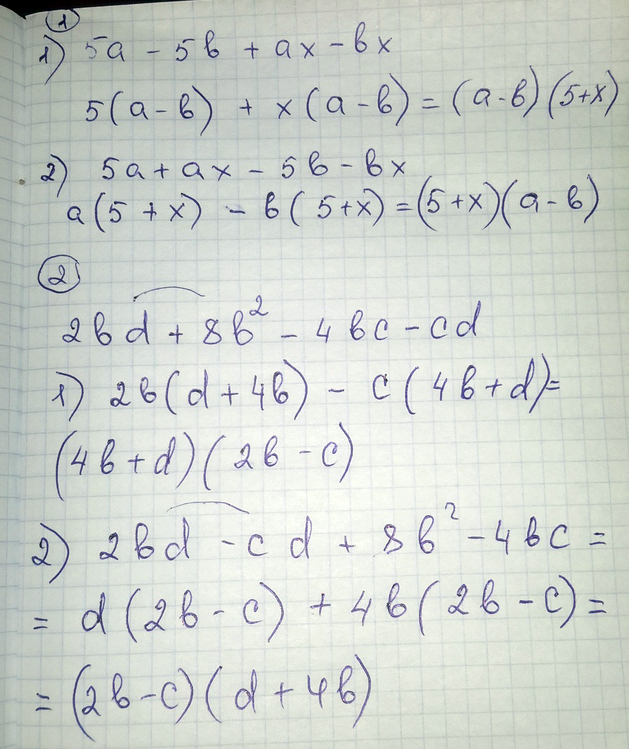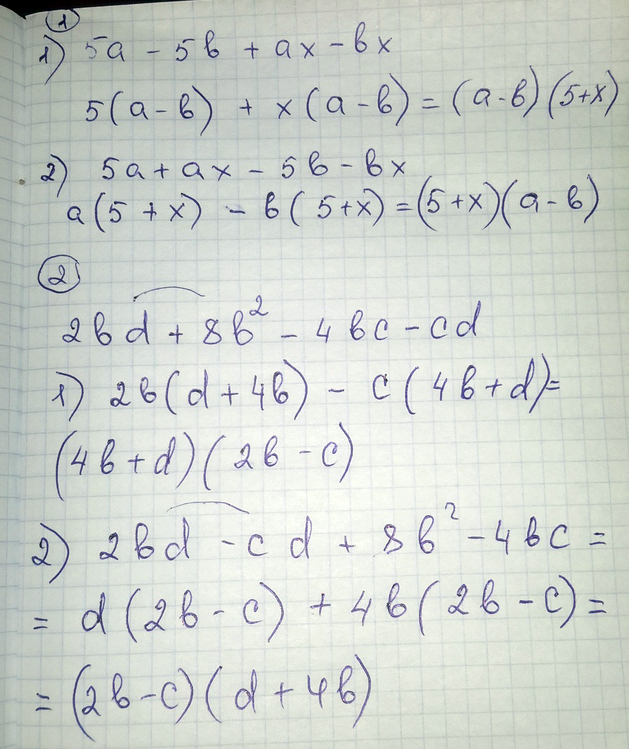представить многочлен в виде произведения - страница 4

1) Разложить на множители
а) 2х(х-1)-3(х-1)
б)ab+ac+4b+4c
2) УПРОСТИТЬ ВЫРАЖЕНИЯ
-0,4а(2а²+3)(5-3а²)
3) ПРЕДСТАВИТЬ МНОГОЧЛЕН В ВИДЕ ПРОИЗВЕДЕНИЯ
а) а²+ab-3a-3b б) kp-kc-px+cx+c-p

Представить многочлен в виде произведения №1) x²-xy-4x+4y=
(№2)ab-ac-bx+cx+c-b=
разложить на множители №1) a(a+3)-2(a+3)=
(№2) ax-ay+5x-5y=
разложите на множители №1) x(x-y)+a(x-y)=
(№2) 2a-2b+ca-cb=
Представить многочлен в виде произведения №1)2a-ac-2c+c²=
(№2) bx+by-x-y-ax-ay=
решите уравнение №1) 9x-6(x-1)-5(x+2) (№2) 7-4(3x-1)=5(1-2x)
упростите выражения№1) 2a(a+b-c)-2b(a-b-c)+2c(a-b+c)=
(№2) 3x(x+y+c)-3y(x-y-c)-3c(x+y-c)=

a(a+3)-2(a+3)=(a-2)(a+3);

ax-ay+5x-5y=a(x-y)+5(x-y)=(a+5)(x-y);

x(x-y)+a(x-y)=(x+a)(x-y);

2a-2b+ca-cb=2(a-b)+c(a-b)=(c+2)(a-b);

$$ 2a-ac-2c+c^2=a(2-c)-c(2-c)=(a-c)(2-c); $$

bx+by-x-y-ax-ay=b(x+y)-1*(x+y)-a(x+y)=(b-1-a)(x+y);

№1) 9x-6(x-1)-5(x+2) -это не уравнение

7-4(3x-1)=5(1-2x);

7-12x+4=5-10x;

-12x+10x=5-7-4;

-2x=-6;

x=-6:(-2);

x=3 - решение

$$ 2a(a+b-c)-2b(a-b-c)+2c(a-b+c)=\\=2a^2+2ab-2ac-2ab+2ab^2+2bc+2ac-2bc+2c^2=2a^2+2b^2+2c^2; \\ 3x(x+y+c)-3y(x-y-c)-3c(x+y-c)=\\=3x^2+3xy+3xc-3xy+3y^2+3yc-3cx-3cy+3c^2=3x^2+3y^2+3c^2; $$

№1) x²-xy-4x+4y=  x(x-y)-4(x-y)=(x-4)(x-y)

(№2)ab-ac-bx+cx+c-b=a(b-c)-x(b-c)-(b-c)=(b-c)(a-x-1)

разложить на множители №1) a(a+3)-2(a+3)= (a-2)(a+3) 

(№2) ax-ay+5x-5y=a(x-y)+5(x-y)=(x-y)(a+5)

разложите на множители №1) x(x-y)+a(x-y)=  (x+a)(x-y)

(№2) 2a-2b+ca-cb=2(a-b)+c(a-b)=(2+c)(a-b)

Представить многочлен в виде произведения №1)2a-ac-2c+c²=a(2-c)-c(2-c)=(a-c)(2-c)

(№2) bx+by-x-y-ax-ay=b(x+y)-(x+y)-a(x+y)=(x+y)(b-1-a)

решите уравнение №1) 9x-6(x-1)=5(x+2)

9x-6x+6=5x+10

3x-5x=4

-2x=4  x=-2

  (№2) 7-4(3x-1)=5(1-2x)

7-12x+4=5-10x

11-5=12x-10x

2x=-6   x=-3

упростите выражения№1) 2a(a+b-c)-2b(a-b-c)+2c(a-b+c)=

2a^2+2ab-2ac-2ab+2b^2+2bc+2ac-2bc+2c^2=2a^2+2b^2+2c^2=2(a^2+b^2+c^2)

(№2) 3x(x+y+c)-3y(x-y-c)-3c(x+y-c)=3x^2+3xy+3xc-3xy+3y^2+3yc-3xc-3yc+3c^2=3(x^2+y^2+c^2)

1. Выполнить умножение:
а)(x-8)*(x+5)= в)(6a+x)*(2a-3x)=
б)(3b-2)*(4b-2)= г)(c+1)*(С"в квадрате"+3с+2)=
2. Разложить на множители:
a)2x(x-1)-3(x-1)=
б)ab+ac+4d+4c=
3. Представьте многочлен в виде произведения:
а)a"в квадрате"+ab-3a-3b=
б) kp-kc-px+cx+c-p=
4. Упростите выражение:
0,4a(2a"в квадрате"+3)(5-3a"в квадрате")

а)2x(x-1)-3(x-1)=(х-1)*(2х-3)

б)ab+ac+4d+4c=а(b+c)+4(d+c)

1.

а) x^2+5x-8x-40=x^2-3x-40

б) 12b^2-6b-8b+4=12b^2-14b+4

в) )12a^2-18ax+2ax-3x^2=12a^2-16ax-3x^2

г) c^3+3c^2+2c+c^2+3c+2=c^3+4c^2+5c+2

( x^2 это значит х "в квадрате" )

( ^ знак степени )

3. 

а) a"в квадрате"+ab-3a-3b= a(a-3)+b(a-3)= (a-3)*(a+b)

б) kp-kc-px+cx+c-p= -k(c-p)+x(c-p)+(c-p)= (c-p)*(x-k+1)

Представить многочлен в виде произведения:
1)3а³-3b³+5a²-5b²
2)a³-b³+a²-b²
3)a^4-a³b+ab³-b^4
Разложите многочлен на множители:
1)(а-b)³+b³
2)(x-2)³-27
3)8a³+(a-b)³
4)27x³-y³(x-y)³

Представить многочлен в виде произведения двучленов сгруппировав по попарно его члены двумя способами 5а -5b +ах - bх. 2 ) 2bd +8b во 2 степени - 4bc- cd=.