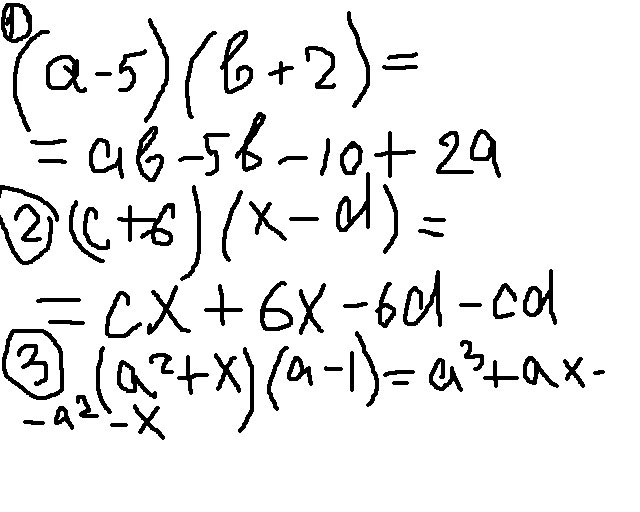многочлен »

представить многочлен в виде произведения - страница 5

  • Представить произведение в виде многочлена: 1) (a-5)*(b+2)
    2) (c+6)*(x-d)
    3) (a^2+x)*(a-1)
    4) (b-2)*(b^2+2b-3)


    Решение: $$ (a-5)*(b+2)=a*b+a*2-5*b-5*2=ab+2a-5b-10 \\ (c+6)*(x-d)=c*x+c*(-d)+6*x+6*(-d)=cx-cd+6x-6d \\ (a^2+x)*(a-1)=a^2*a+a^2*(-1)+x*a+x*(-1)=a^3-a^2+ax-x \\ (b-2)(b^2+2b-3)=b*b^2+b*2b+b*(-3)-2*b^2-2*2b-2*(-3)=\\=b^3+2b^2-3b-2b^2-4b+6=b^3-7b+6 $$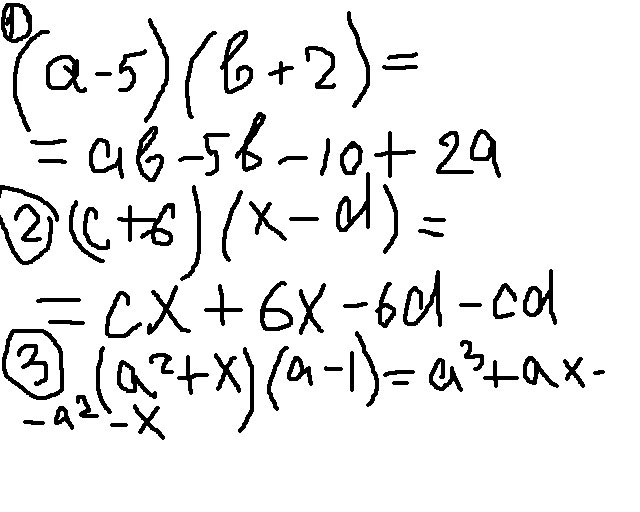

    a- b a b a - b- ab a- b- c x-d c x c -d x -d cx-cd x- d a x a- a a a - x a x - a -a ax-x b- b b- b b b b b - - b - b- - b b - b- b - b b - b...

  • Помогите представить в виде произведения многочлен:
    1) a³+a²-a-1;
    2) 2х³-2хy²-8х²+8y²;
    3) 5а²-5b²-15а³b+15аb³;
    4) а²b²-1-b²+a².


    Решение: 1) ( a^3 - 1) + (a^2 - a) = (a - 1)(a^2 + a + 1) + a(a - 1) = (a - 1)(a^2+a+1+a)=
    = ( a - 1)(a^2 + 2a + 1)
    2) (2x^3 - 2xy^2) - 8( x^2 - y^2) = 2x( x^2 - y^2) - 8(x^2 - y^2) =
    = ( x^2 - y^2)(2x - 8) = 2(x + y)(x - y)(x - 4)
    3) (5a^2 - 5b^2) - 15ab(a^2 - b^2) = 5(a^2 - b^2) - 15ab(a^2 - b^2) =
    = (a^2 - b^2)( 5 - 15ab) = 5(a- b)(a + b)( 1 - 3ab)
    4) (a^2b^2 - b^2) + (a^2 - 1) = b^2(a^2 - 1) + (a^2 - 1) = (a^2 - 1)(b^2 +1)=
    = (a - 1)(a+ 1)(b^2 + 1)
    )))

  • 1) Представьте в виде произведения многочлен
    x(b+c)+3b+3c
    y(a-c)+5a-5c
    p(c-d)+c-d
    a(p-q)+q-p
    2) Решите уравнение
    а) 4-x(x+8)=11-x² b) 4x(3x-1)-2x(6x+8)=5


    Решение: Задание № 1

    $$ x(b+c)+3b+3c=\\=x(b+c)+(3b+3c)=x(b+c)+3(b+c)=(b+c)(x+3) \\ y(a-c)+5a-5c=y(a-c)+(5a-5c)=y(a-c)+5(a-c)=(a-c)(y+5) $$

    $$ p(c-d)+c-d=p(c-d)+(c-d)=p(c-d)+1(c-d)=(c-d)(p+1) $$

    $$ a(p-q)+q-p=a(p-q)-p+q=a(p-q)+(-p+q)=\\=a(p-q)-(p-q)=a(p-q)-1(p-q)=(p-q)(a-1) $$

    Задание № 2

    а) $$ 4-x(x+8)=11-x^{2} \\ 4-x^{2}-8x=11-x^{2} \\ 4-x^{2}-8x-11+x^{2}=0 \\ -8x-7=0 \\ 8x=-7 \\ x=-7:8 \\ x=-\frac{7}{8} $$

    б) $$ 4x(3x-1)-2x(6x+8)=5 \\ 12x^{2}-4x-12x^{2}-16x=5 \\ (12x^{2}-12x^{2})+(-4x-16x)=5 \\ -4x-16x=5 \\ -20x=5 \\ x=5:(-20) \\ x=-\frac{1}{4}=-0,25 $$

  • Как представить многочлен в виде произведения?


    Решение: Если многочлен во второй степени, вроде ах²+bx+c, то просто приравниваете к нулю по формуле Виета находите корни
    х1+х2=-b/a и
    x1*x2=c/a,
    либо через дискриминант D=b²-4*a*c, x1,x2=(-b+-√D)/2a. Найдя корни, раскладываете (x-x1)*(x-x2).
    Если же степень больше, то попробуй методом группировки, создавая одинаковые скобки, которые потом выносите как общий множитель и получается то же самое произведение. Еще есть вариант по схеме Горнера, но там легко запутаться...

  • Представьте многочлен x^4-3x^2+1 в виде произведения.
    Вычислите
    12,5^2+1,2^2- (12,5^3+1,2^3/13,7 дробь)


    Решение: $$ x^4-3x^2+1=x^4-x^3-x^2+x^3-x^2-x-x^2+x+1= \\ =x^2(x^2-x-1)+x(x^2-x-1)-1(x^2-x-1)= \\ =(x^2+x-1)(x^2-x-1) \\ 12,5^2+1,2^2-[(12,5^3+1,2^3):13,7]= \\ \\ =(\frac{125}{10})^2+(\frac{12}{10})^2-[((\frac{125}{10})^3+(\frac{12}{10})^3):\frac{137}{10}]= \\ \\ =(\frac{25}{2})^2+(\frac{6}{5})^2-[((\frac{25}{2})^3+(\frac{6}{5})^3):\frac{137}{10}]= \\ \\ =\frac{625}{4}+\frac{36}{25}-[(\frac{15625}{8}+\frac{216}{125}):\frac{137}{10}]= \\ \\ =\frac{625*25+36*4}{100}-[\frac{15625*125+216*8}{1000}:\frac{137}{10}]= \\ \\ =\frac{15769}{100}-[\frac{1954853}{1000}:\frac{137}{10}]= \\ =\frac{15769}{100}-[\frac{1954853}{1000}*\frac{10}{137}]= \\ \\ =\frac{15769}{100}-\frac{14269}{100}= \frac{1500}{100}=15 $$

<< < 345 6 7 > >>