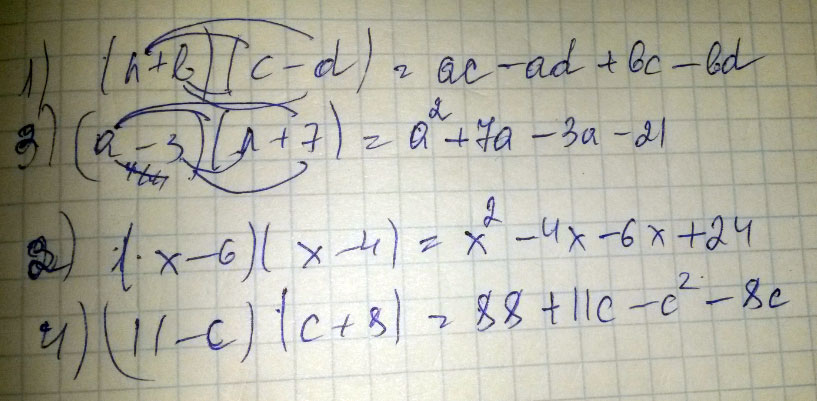многочлен n-й степени - страница 6

1. Упростите вырожение (х-3)в кваадрате+х(х=9)= 2.b в квадрате=49-(b-7)вквадрате= 3 Разложите на мнодители многочлен b в 6 степени-3b в 4 степени-2bв квадрате+6= 4.хв квадрате+6х+5= СПАСИБО

(x-3)(x+3) + x2 + 9x 

X2- 9-3x -9

2x2+6x

1) (х-3) в квадрате +х(х+9)= хв квадрате +9-6х+хв квадрате+9=2хв квадрате -6х+18= х в квадрате - 3х +9

2) в в вквадрате +49 -(в-7)в квадрате= в в квадрате +49 - ( в в квадрате +49 - 14в)= в в квадрате +49 - в в квадрате -49 +14в= 14в

3) в в 6 степени - зв в 4 степени - 2в в квадрате +6= в в 4 степени( в в квадрате - 3) -2( в в квадрате - 3)= (в в 4 степени -2)(в в квадрате - 3)

Разложите на множители многочлен: 1) (х(во 2й степени) - 4) + (2+х)
2) (х( во 2й степени) -9) +(3+х)

1. (x² - 4) + (2 + х) = (х - 2)(х + 2) + (х + 2) = (х - 2 + 1)(х + 2) = (х - 1)(х + 2). Первое слагаемое - это разность квадратов чисел х и 2, то есть (x² - 4). После выделения множителей у разности квадратов мы выносим за скобку общий множитель. 2. (х² - 9) + (3 + х) = (х - 3)(х + 3) + (х + 3) = (х - 3 + 1)(х + 3). Первое слагаемое - разность квадратов чисел х и 3, то есть (х² - 9). Опять-таки после разложения разности квадратов на множители выносим общий множитель за скобку.

Определите многочлен А и найдите его степень, используя правила нахождения неизвестного слагаемого, уменьшаемого и вычитаемого.


а) А+(12у^2+6y-1)=-10+9
б) (-6x^2+7x-11)-A=2x^2+2x-1
в) A-(6a^2_5ab+b^3)=4b^3-11ab
г) (25x^5-13x^3+7)+A=15x^5-13x^2

В многочлен: 1 (а+b)(c-d) 2 (x-6)(x-4)
3 (a-3)(a+7)
4 (11-c)(c+8)
5 (d+13)(2d-1)
6 (3y-5)(2y-12)
7 2x(2-й степени)-3)(х(2-й степени)+4)
8 (х-6)(х(2-й)-2х+9)
9 (5х-у)(2х(2-й)+ху-3у(2-й))
10 b(6b+7)(3b-4)

7 2x(2-й степени)-3)(х(2-й степени)+4) 
8 (х-6)(х(2-й)-2х+9) 
9 (5х-у)(2х(2-й)+ху-3у(2-й)) 
10 b(6b+7)(3b-4) 

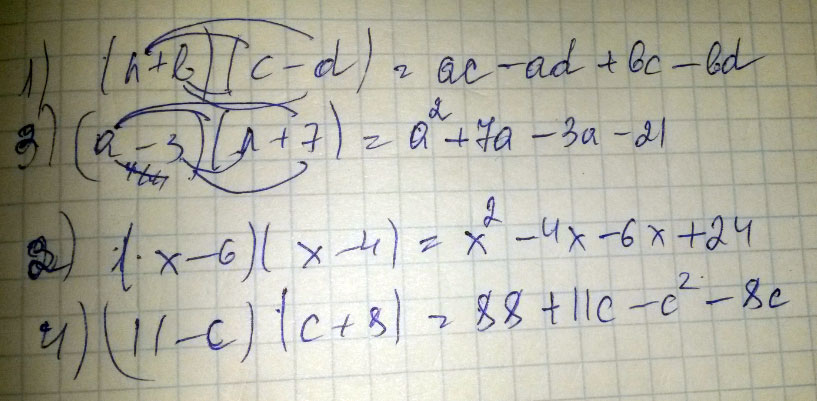
Разложить многочлены на множители: а4(а в 4 степени) – а2(а во 2 степени) + 6а +6 х2 ( х во 2 степени)– 9 – 2ах – 6а

Где первая скобка - это формула. (a^2-1)=(a-1)(a+1). Используем это:
a^2*(a-1)*(a+1)+6*(a+1)
Выносим общую часть:
(a+1)*(a^2*(a-1)+6)

x^2-9-2ax-6a=(x-3)(x+3)-2a*(x+3)=(x+3)(x-3-2a)