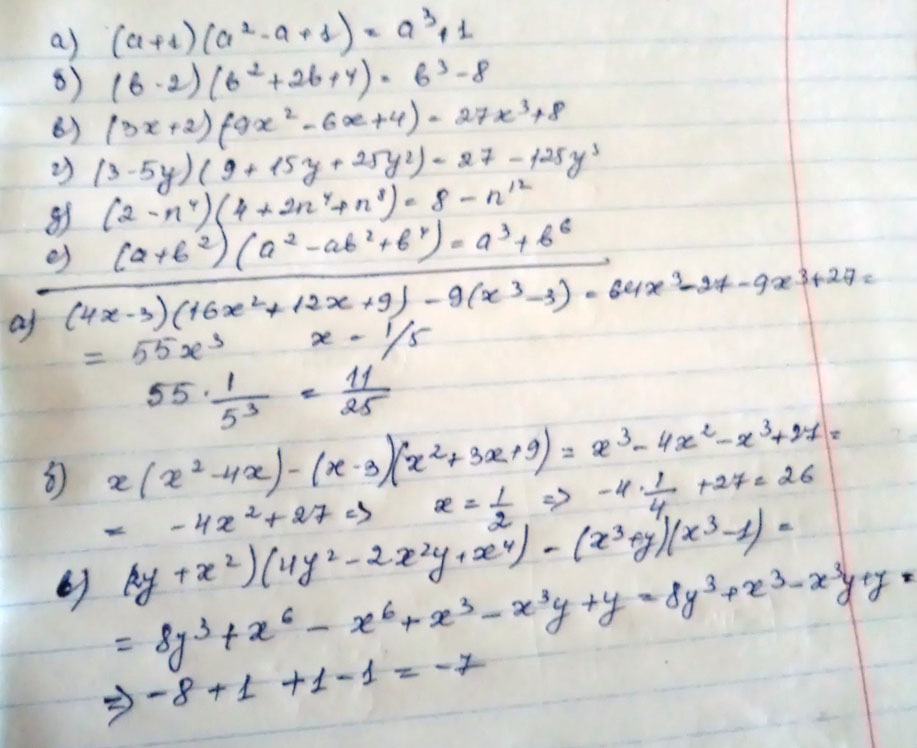преобразуйте выражение в многочлен
Упростите выражение. а) 2c(5c-3)-(c-2)(c-4) б) (a-4)(a+6)+(a-10)(a-2). Преобразуйте в многочлен. а) (y-2)(y+3)-(y-1)^2 ( ^-степень) б) 4(а+5)^2-(4a^2+40a)
Решение: a)2c(5c-3)-(c-2)(c-4) a)(y-2)(y+3)-(y-1)²=3y-710c²-6-(c²-6c+8) 4(a+5)²-(4a²+40a)
10c²-6-c²+6c-8 4(a²10a+25)-(4a²+40a)
9c²-14+6c 4a²+40a+100-4a²-40a=100
b)(a-4)(a+6)+(a-10)(a-2)
a²+2a-24+a²-12a+20
2a²-10a-4
$$ 2c(5c-3)-(c-2)(c-4)=10c^2-6c-c^2+4c+2c-8=9c^2-8 $$
$$ (a-4)(a+6)+(a-10)(a-2)=\\=a^2+6a-4a-24+a^2-10a-2a+20=2a^2-10a-4 $$
$$ (y-2)(y+3)-(y-1)^2=\\=y^2-2y+3y-6-y^2+2y-1=3y-7 $$
$$ 4(a+5)^2-(4a^2+40a)=\\=4a^2+40a+100-4a^2-40a=100 $$
1. Преобразуйте в многочлен. а) (2х-1)(Единица во второй степени) б) (3а +с) (С во второй степени) в)(у-5)(у+5) г) (4b+5c)(4b-5c) 2.Упростите выражение. (х+у)(х-у)-(Х во второй степени) + 3у(У во второй степени) 3.Разложите на множители а) 16у(во второй степени) - 0.25 б) а(во второй степени) +10аb+25b(во второй степени)
Решение: 1.а)=1*(2х-1)=2х-1б)=с^2*(3a+c)=3ac^2+c^3
в)=y^2-25
г)=16b^2-25c^2
2.=x^2-y^2-x^2+3y^3=3y^3-y^2=y^2(3y-1)
3.а)=16y^2-0.25=(4y-0.5)(4y+0.5)
б)=a^2+10ab+25b^2=(a+5b)(a+5b)
P.S. y^2 значит игрик в квадрате
1.
а) (2х-1)(1^2)=2х-1
б) (3a+c)*с^2 =3ac^2+c^3
в) y^2-25
г) 16b^2-25c^2
2.x^2-y^2-x^2+3y^3=3y^3-y^2=y^2(3y-1)
3.а) 16y^2-0.25=(4y-0,5)(4y+0,5)
б) a^2+10ab+25b^2=(a+5b)(a+5b)1.Чему равен остаток при делении многочлена Q(X;Y)=(x-2y)в десятой степени+5(x-2y)в четвёртой степени+(x-2y+5)в квадрате -14 на двучлен x-2y. 2.Преобразуйте в многочлен выражение (а-3)(а+1)-(а+6)в 3 степени
Решение:первые два слагаемых нацело разделятся на двучлен (т.е. без остатка)...
остаток возникнет только при делении (х-2y+5)^2 - 14
раскроем скобки: (x-2y)^2 + 10(x-2y) + 25 - 14
и вновь первые два слагаемых разделятся на (х-2у) нацело
а остаток будет = 25-14 = 11
-------------------------------------------
А здесь нужно просто раскрыть скобки и привести подобные...
a^2 - 2a - 3 - a^3 - 18a^2 - 108a - 216 = -a^3 - 17a^2 - 110a - 219
1) Преобразуйте данное выражение в многочлен:
а) (а+1)(а^2-а+1)=
б)(b-2)(b^2+2b+4)=
в) (3x+2)(9x^2-6x+4)=
г) (3-5y)(9+15y+25y^2)
д) (2-n^4)(4+2n^4+n^8)=
е)(a+b^2)(a^2-ab^2+b^4)=
2) Упростите выражение и найдите его значение:
а) (4x-3)(16x^2+12x+9)-9(x^3-3) при х= 1/5
б) x(x^2-4x)-(x-3)(x^2+3x+9) при х=1/2
в) (2y+x^2)(4y^2-2x^2y+x^4)-(x^3+y)(x^3-1) при х=1, у= -1
Решение: 1) Преобразуйте данное выражение в многочлен:
а) (а+1)(а^2-а+1)=a³+1
б)(b-2)(b^2+2b+4)=b³-8
в) (3x+2)(9x^2-6x+4)=27x³+8
г) (3-5y)(9+15y+25y^2)=27-125y³
д) (2-n^4)(4+2n^4+n^8)=8-n^12
е)(a+b^2)(a^2-ab^2+b^4)=a³+b^6
2) Упростите выражение и найдите его значение:
а) (4x-3)(16x^2+12x+9)-9(x^3-3) при х= 1/5
64x³-27-9x³+27=55x³ 55/125=11/25
б) x(x^2-4x)-(x-3)(x^2+3x+9) при х=1/2
x³-4x²-x³+27=27-4x² 27-4*1/4=26
в) (2y+x^2)(4y^2-2x^2y+x^4)-(x^3+y)(x^3-1) при х=1, у= -1
8y³+x^6-x^6-yx^3+x^3+y -8+1-1+1+1-1=-7
(2y+x^2)(4y^2-2x^2y+x^4)-(x^3+1)(x^3-1) при х=1, у= -1
8y³+x^6-x^6+1=8y³+1 -8+1--7
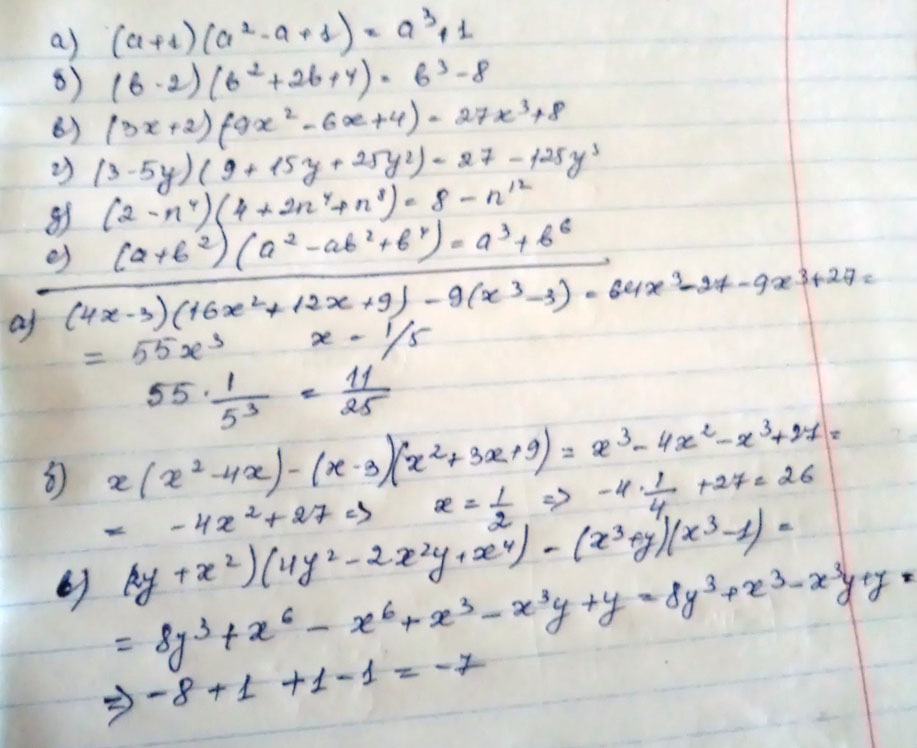
1. Преобразуйте в многочлен выражение: (3х – 2у)(х + у) – 3х².
2. Упростите выражение: 7а(а – b) – 3(b – a)²
3. Разложите на множители: 18ху² - 2хz²
4. Представьте в виде произведения: ху^4 - у^4 + ху³ - у³(^4- в 4 степени)
5. Найдите значение выражения (6а – 1)(6а + 1) – (12а – 5)(3а + 1) при а=0,2
6. Выполните возведение в квадрат (7b + b^5 )²
7. Возведите в куб двучлен: 3х + 2
8. Замените знак таким одночленом, чтобы полученное выражение можно было представить в виде квадрата двучлена: - 28pq + 49q²
9. Найдите корень уравнения (6х – 1)(6х + 1) – 9х(4х + 2) = 2
10. Разложите на множители 100 - k^6(в 6 степени)
11. Вычислите 599², используя формулу квадрата разности
12. Вычислите значение выражения 2001² - 1999²
13. Упростите выражение (1 – 3х)(1 – 4х + х²) + (3х – 1)(1 – 5х + х²) + 3х²
14. Найдите значение х из условия (х + 2)(х² - 2х + 4) = 16
Решение: 1.
=3х²+3ху-2ху-2у²-3х²=ху-2у²
2.
=7(а-б)+3(а-б)²=(а-б)(7+3(а-б))=(а-б)(7+3а-3б)
а если разложить на множители то тогда
=7а²-7б-3б²-6аб+3а²=10а²-7б-3б²-6аб
3.
=2х(9у²-z²)=2х(3у-z)(3у+z)
4.
=у∧4(х-1)+у∧3(х-1)=(х-1)(у∧4-у∧3)=у∧3(х-1)(у-1)
∧4 в четвертой степени
5.
=36а²-1-36а²-12а+15а+5=3а+4=3*0,2+4=4,6
6.
=49б²+14б∧6+б∧10
7.
(3х+2)³=27х³+54х²+36а+8
9.
36х²-1-36х²-18х=2
-1-18х=2
-18х=2+1
-18х=3
х=3÷(-18)
х=-1/6
10.
100-к∧6=(10-к∧3)(10+к∧3)
12.
=(2001-1999)(2001+1999)=2*4000=80001) Преобразуйте выражение (2х-1)^2-4(x+1) в многочлен стандартного вида
2)Представьте уравнение х^3/x^-5 * x^2 в виде степени к основанием х
3)Решите уравнение 4(х-2)=х+7
Решение: 1) (2х-1)² - 4(x+1) =
4х² - 4х + 1 - 4х - 4 =
4х² - 8х - 3
2) на фото
3) 4(х-2) = х + 7
4х - 8 = х + 7
3х = 15
х = 5
1) (2х-1)²-4(x+1)=4х²-4х+1-4х-4=4х²-8х-3
2) х³/x⁻⁵ * x²=х³⁺⁵ * х²=х⁸ * х²=х⁸⁺²=х¹⁰
3)4(х-2)=х+7
4х-8=х+7
4х-х=7+8
3х=15
х=15/3=5
отв:5
1. Преобразуйте в многочлен:
а) 4х(2х – 1) – (х – 3)(х + 3)
б) (х + 3)(х – 11) + (х + 6)2
в) 7(а + b) 2 – 14аb
2. Разложите на множители:
а) у3 - 49у б) -3а2 – 6аb - 3b2
3. Найдите значение выражения а2 – 4bс, если а = 6, b = -11, с = -10
4. Упростите выражение:
(а - 1)2 (а + 1) + (а + 1)( а - 1)
5. Докажите тождество:
(х - у)2 + (х + у)2 = 2(х2 + у2)
Решение: 1.
a)8x²-4x-(x²-9)=8x²-4x-x²+9
=7x²-4x+9
b) x²-11x+3x-33+x²+12x+36=
=2x²+4x+3
v) 7(a²+2ab+b²)-14ab=
=7a²+14ab+7b²-14ab=
=7(a²+b²)
2. a) y(y²-49)=y(y-7)(y+7)
b) -3(a²+2ab+b²)= -3(a+b)²
3. a²-4bc=36-4(-11)*(-10)=
=36-440= -404
4. (a-1)²(a+1)+(a+1)(a-1)=
=(a-1)(a²-1)+(a²-1)=(a-1)(a²-1-1)
=(a-1)(a²-2)
5. (x-y)²+(x+y)²=2(x²+y²)
x²-2xy+y²+x²+2xy+y²=
=2(x²+y²)
2x²+2y²=2(x²+y²)
2(x²+y²)=2(x²+y²)
чтд
Преобразуйте в многочлен:
а) 4х(2х – 1) – (х – 3)(х + 3); в) 7(а + b)2 – 14аb.
б) (р + 3)(р – 11) + (р + 6)2;
2. Разложите на множители:
а) у3 – 49у; б) –3а2 – 6ab – 3b2.
3. Упростите выражение (а – l)2(a + 1) + (а + 1)(а – 1) и найдите его значение при а = – 3.
4. Представьте в виде произведения:
а) (у – 6)2 – 9у2; б) с2 – d 2 – с + d.
5. Докажите тождество (х – у)2 + (х + у)2 = 2(х 2 + у 2).
Решение: 1) 8x^2 - 4x - ( x^2 - 9) = 8x^2 - 4x - x^2 + 9= 7x^2 - 4x + 9
p^2 - 8p - 33 + p^2 + 12p + 36 = 2p^2 + 4p + 3
7( a^2 + 2ab + b^2) - 14ab = 7a^2 + 14ab + 7b^2 - 14ab = 7a^2 + 7b^2
2) y^3 - 49y = y( y^2 - 49) = y( y - 7)(y + 7)
- 3( a^2 + 2ab + b^2) = - 3(a + b)^2 = - 3( a + b)(a + b)
3) 2( a - 1)( a + 1) +( a + 1)(a - `1) = (a^2 - 1)(2 + 1) = 3(a^2 - 1) = 3a^2 - 3
При a = - 3:
3a^2 - 3 = 3*(-3)^2 - 3 = 27 - 3 = 24
4) ( y - 6 + 3y)(y - 6 - 3y) = ( 4y - 6)( - 2y - 6)
( c - d)(c + d) - (c - d) = ( c - d)( c + d - 1)
5) ( x - y)^2 + ( x + y)^2 = 2( x^2 + y^2)
x^2 - 2xy + y^2 + x^2 + 2xy + y^2 = 2x^2 + 2y^2
2x^2 + 2y^2 = 2x^2 + 2y^2 - верно, тождество доказаноВыражение (а + 1/а)^3 преобразуйте в многочлен, используя полученное тождество, найдите значение выражения а^3 + 1/а^3 при условии а + 1/а =5.
Решение: Применим формулу куба суммы. Там часть множителей сократиться. Оттуда можно вычислить искомое выражение.(a+1/a)³=a³+3a²×1/a+3a×1/a²+1/a³=a³+3a+3/a+1/a³=a³+1/a³+3(a+1/a);
a³+1/a³=(a+1/a)³-3(a+1/a)
a³+1/a³=5³-3×5=125-15=110
1. Преобразуйте в многочлен:
а) (а – 2)( а + 2) – 2а(5 – а)
б) (у – 9)2 – 3у(у + 1)
в) 3(х – 4) 2 – 3х22. Разложите на множители:
а) 25х – х3 б) 2х2 – 20х + 503. Найдите значение выражения а2 – 4bс, если а = 6, b = -11, с = -10
а) 452 б) -202 в) -404 г) 4764. Упростите выражение:
(с2 – b)2 – (с2 - 1)(с2 + 1) + 2bс25. Докажите тождество:
(а + b)2 – (а – b)2 = 4аb
Решение: Преобразуйте в многочлен:
а) (а – 2)( а + 2) – 2а(5 – а) =а^2-4-10a+2a^2=6a^2-10a-4
б) (у – 9)2 – 3у(у + 1) =y^2-18y+81-3y^2-3y=-2y^2-21y+81
в) 3(х – 4) 2 – 3х2 =3(x^2-8x+16)-3x^2=3x^2-24x+48-3x^2=48-24x
2. Разложите на множители:
а) 25х – х3=x(25-x^2)=x(5-x)(5+x)б) 2х2 – 20х + 50 =2(x^2-10x+25)=2(x-5)^2=2(x-5)(x+5)
3. Найдите значение выражения а2 – 4bс=36-4*(-11)*(-10)=36-440=-404
а) 452 б) -202 в) -404 г) 476
4. Упростите выражение:
(с2 – b)2 – (с2 - 1)(с2 + 1) + 2bс2 =c^4-4bc^2+b^2-c^4+1=-4bc^2+b^2+1
5. Докажите тождество:
(а + b)2 – (а – b)2 = 4аba^2+2ab+b^2-a^2+2ab-b^2=2a+2ab=4ab
2. а/ (5-х) х*(х+5); б/ 2(x-5)^2;
4. b^2+1.
