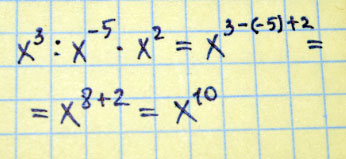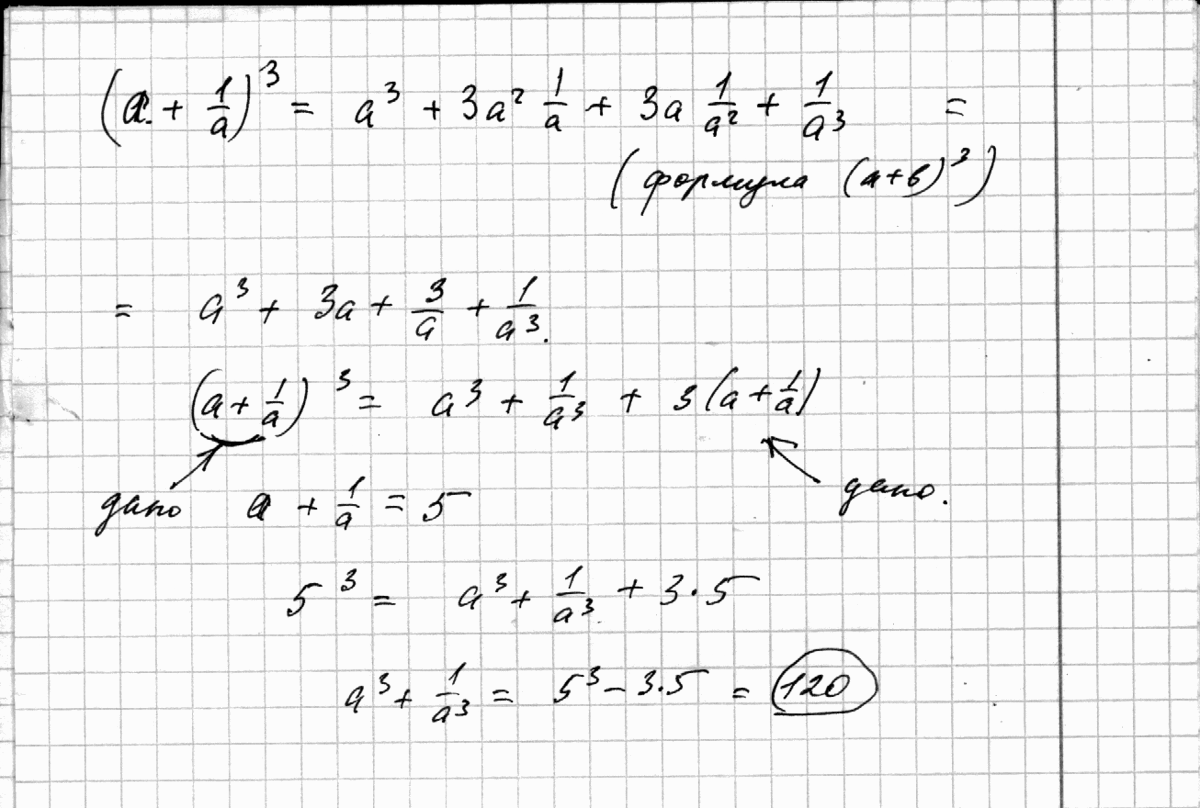многочлен »

преобразуйте выражение в многочлен - страница 2

  • 1) Преобразуйте выражение (2х-1)^2-4(x+1) в многочлен стандартного вида

    2)Представьте уравнение х^3/x^-5 * x^2 в виде степени к основанием х

    3)Решите уравнение 4(х-2)=х+7


    Решение: 1) (2х-1)² - 4(x+1) =
    4х² - 4х + 1 - 4х - 4 =
    4х² - 8х - 3

    2) на фото

    3)     4(х-2) = х + 7
    4х - 8 = х + 7
    3х = 15
    х = 5

    1) (2х-1)²-4(x+1)=4х²-4х+1-4х-4=4х²-8х-3
    2) х³/x⁻⁵ * x²=х³⁺⁵ * х²=х⁸ * х²=х⁸⁺²=х¹⁰
    3)4(х-2)=х+7
    4х-8=х+7
    4х-х=7+8
    3х=15
    х=15/3=5
    отв:5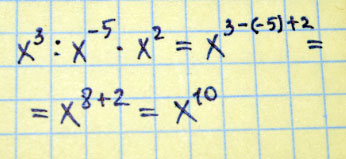     х- - x х - х - х - х - х - на фото х- х х - х х х   х- - x х - х - х- х - х-  х x   x х х х х х х х- х х- х х-х х х отв...

  • 1. Преобразуйте в многочлен:
    а) 4х(2х – 1) – (х – 3)(х + 3)
    б) (х + 3)(х – 11) + (х + 6)2
    в) 7(а + b) 2 – 14аb
    2. Разложите на множители:
    а) у3 - 49у б) -3а2 – 6аb - 3b2
    3. Найдите значение выражения а2 – 4bс, если а = 6, b = -11, с = -10
    4. Упростите выражение:
    (а - 1)2 (а + 1) + (а + 1)( а - 1)
    5. Докажите тождество:
    (х - у)2 + (х + у)2 = 2(х2 + у2)


    Решение: 1.
    a)8x²-4x-(x²-9)=8x²-4x-x²+9
    =7x²-4x+9
    b) x²-11x+3x-33+x²+12x+36=
    =2x²+4x+3
    v) 7(a²+2ab+b²)-14ab=
    =7a²+14ab+7b²-14ab=
    =7(a²+b²)
    2. a) y(y²-49)=y(y-7)(y+7)
    b) -3(a²+2ab+b²)= -3(a+b)²
    3. a²-4bc=36-4(-11)*(-10)=
    =36-440= -404
    4. (a-1)²(a+1)+(a+1)(a-1)=
    =(a-1)(a²-1)+(a²-1)=(a-1)(a²-1-1)
    =(a-1)(a²-2)
    5. (x-y)²+(x+y)²=2(x²+y²)
    x²-2xy+y²+x²+2xy+y²=
    =2(x²+y²)
    2x²+2y²=2(x²+y²)
    2(x²+y²)=2(x²+y²)
    чтд

  • Преобразуйте в многочлен:
    а) 4х(2х – 1) – (х – 3)(х + 3); в) 7(а + b)2 – 14аb.
    б) (р + 3)(р – 11) + (р + 6)2;
    2. Разложите на множители:
    а) у3 – 49у; б) –3а2 – 6ab – 3b2.
    3. Упростите выражение (а – l)2(a + 1) + (а + 1)(а – 1) и найдите его значение при а = – 3.
    4. Представьте в виде произведения:
    а) (у – 6)2 – 9у2; б) с2 – d 2 – с + d.
    5. Докажите тождество (х – у)2 + (х + у)2 = 2(х 2 + у 2).


    Решение: 1) 8x^2 - 4x - ( x^2 - 9) = 8x^2 - 4x - x^2 + 9= 7x^2 - 4x + 9
    p^2 - 8p - 33 + p^2 + 12p + 36 = 2p^2 + 4p + 3
    7( a^2 + 2ab + b^2) - 14ab = 7a^2 + 14ab + 7b^2 - 14ab = 7a^2 + 7b^2
    2) y^3 - 49y = y( y^2 - 49) = y( y - 7)(y + 7)
    - 3( a^2 + 2ab + b^2) = - 3(a + b)^2 = - 3( a + b)(a + b)
    3) 2( a - 1)( a + 1) +( a + 1)(a - `1) = (a^2 - 1)(2 + 1) = 3(a^2 - 1) = 3a^2 - 3
    При a = - 3:
    3a^2 - 3 = 3*(-3)^2 - 3 = 27 - 3 = 24
    4) ( y - 6 + 3y)(y - 6 - 3y) = ( 4y - 6)( - 2y - 6)
    ( c - d)(c + d) - (c - d) = ( c - d)( c + d - 1)
    5) ( x - y)^2 + ( x + y)^2 = 2( x^2 + y^2)
    x^2 - 2xy + y^2 + x^2 + 2xy + y^2 = 2x^2 + 2y^2
    2x^2 + 2y^2 = 2x^2 + 2y^2 - верно, тождество доказано

  • Выражение (а + 1/а)^3 преобразуйте в многочлен, используя полученное тождество, найдите значение выражения а^3 + 1/а^3 при условии а + 1/а =5.


    Решение: Применим формулу куба суммы. Там часть множителей сократиться. Оттуда можно вычислить искомое выражение.

    (a+1/a)³=a³+3a²×1/a+3a×1/a²+1/a³=a³+3a+3/a+1/a³=a³+1/a³+3(a+1/a);
    a³+1/a³=(a+1/a)³-3(a+1/a)
    a³+1/a³=5³-3×5=125-15=110

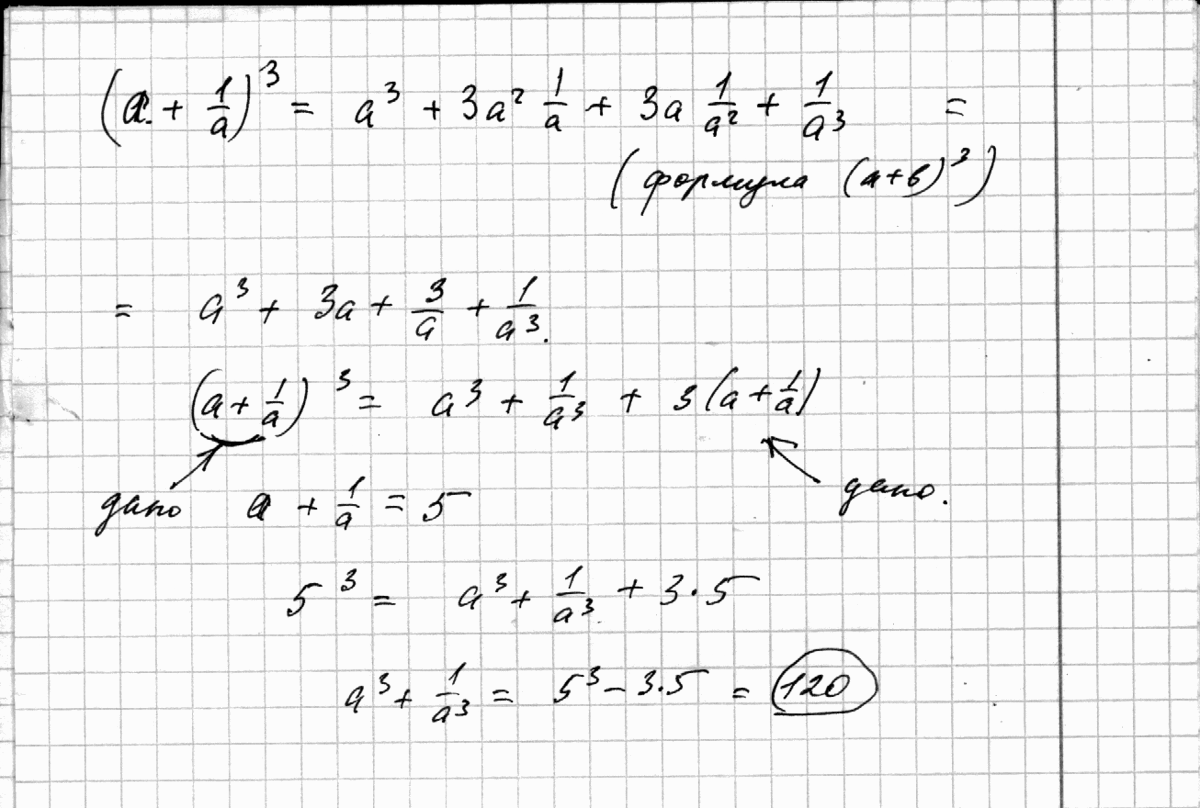
    Применим формулу куба суммы. Там часть множителей сократиться. Оттуда можно вычислить искомое выражение. a a a a a a a a a a a a a a a a a a a a - a a a a - -...

  • 1. Преобразуйте в многочлен:
    а) (а – 2)( а + 2) – 2а(5 – а)
    б) (у – 9)2 – 3у(у + 1)
    в) 3(х – 4) 2 – 3х2

    2. Разложите на множители:
    а) 25х – х3 б) 2х2 – 20х + 50

    3. Найдите значение выражения а2 – 4bс, если а = 6, b = -11, с = -10
    а) 452 б) -202 в) -404 г) 476

    4. Упростите выражение:
    (с2 – b)2 – (с2 - 1)(с2 + 1) + 2bс2

    5. Докажите тождество:
    (а + b)2 – (а – b)2 = 4аb


    Решение: Преобразуйте в многочлен:
     а) (а – 2)( а + 2) – 2а(5 – а) =а^2-4-10a+2a^2=6a^2-10a-4
     б) (у – 9)2 – 3у(у + 1) =y^2-18y+81-3y^2-3y=-2y^2-21y+81
     в) 3(х – 4) 2 – 3х2 =3(x^2-8x+16)-3x^2=3x^2-24x+48-3x^2=48-24x
    2. Разложите на множители:
     а) 25х – х3=x(25-x^2)=x(5-x)(5+x)

     б) 2х2 – 20х + 50 =2(x^2-10x+25)=2(x-5)^2=2(x-5)(x+5)
     3. Найдите значение выражения а2 – 4bс=36-4*(-11)*(-10)=36-440=-404
     а) 452 б) -202 в) -404 г) 476 
    4. Упростите выражение:
     (с2 – b)2 – (с2 - 1)(с2 + 1) + 2bс2 =c^4-4bc^2+b^2-c^4+1=-4bc^2+b^2+1
    5. Докажите тождество:
    (а + b)2 – (а – b)2 = 4аb

    a^2+2ab+b^2-a^2+2ab-b^2=2a+2ab=4ab 

    2. а/ (5-х) х*(х+5); б/ 2(x-5)^2;

    4. b^2+1.

<< < 12 3 4 > >>