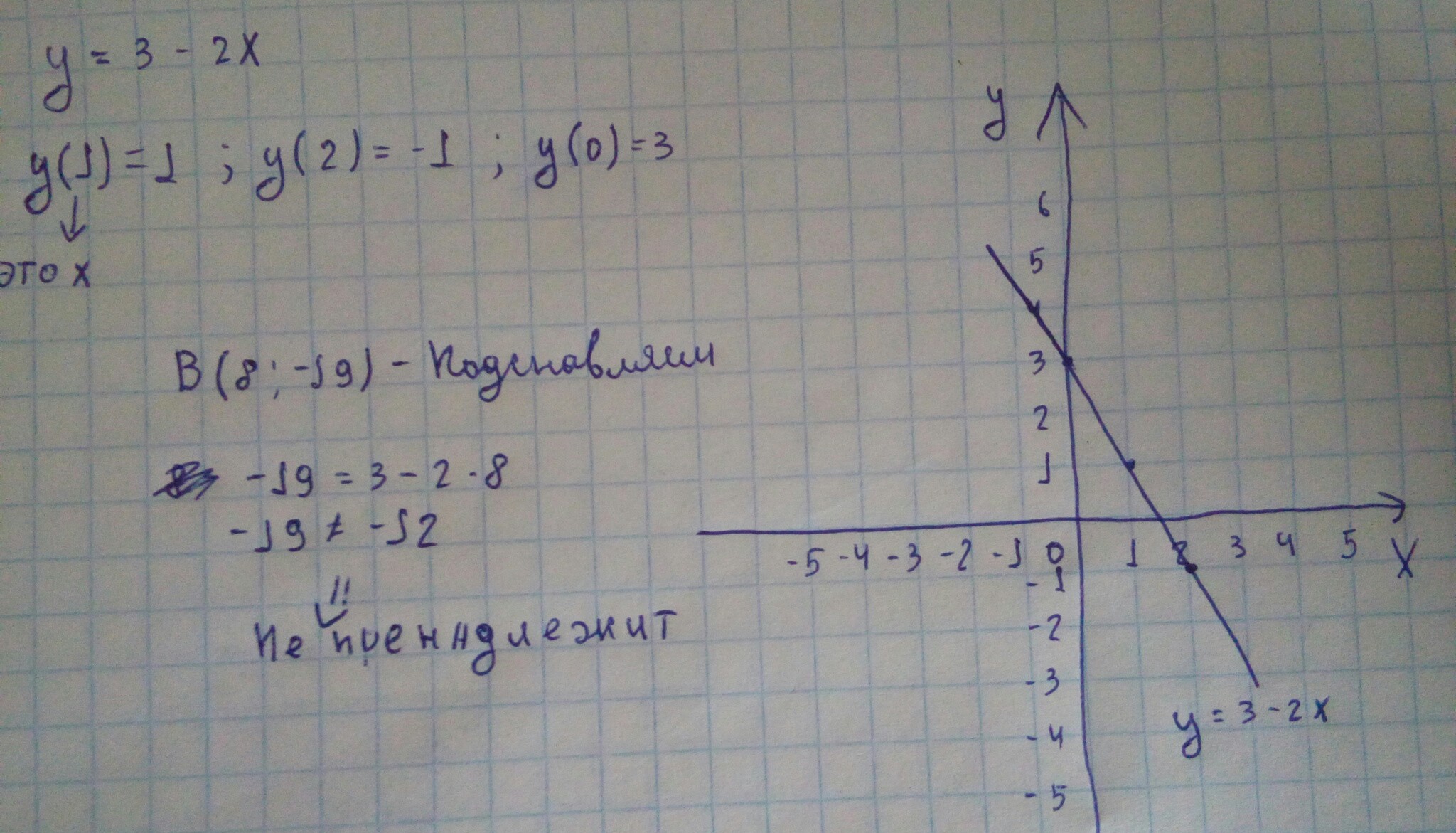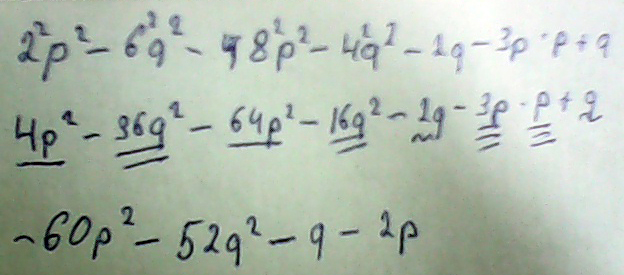преобразуйте выражение в многочлен стандартного вида - страница 4

1) преобразуйте многочлен стандартного вида
а)(x+4y)(4y-x)
б)2t(t+8)-(t-6) в квадрате
2) решите уравнения
6x-(2x+5)=2(3-6)
3) решите систему уравнений
3x+5y=-9
4x+y=5
4) постройте график функций
y=3-2x принадлежит ли этому гаф. ку этой функции точка B(8;-19)

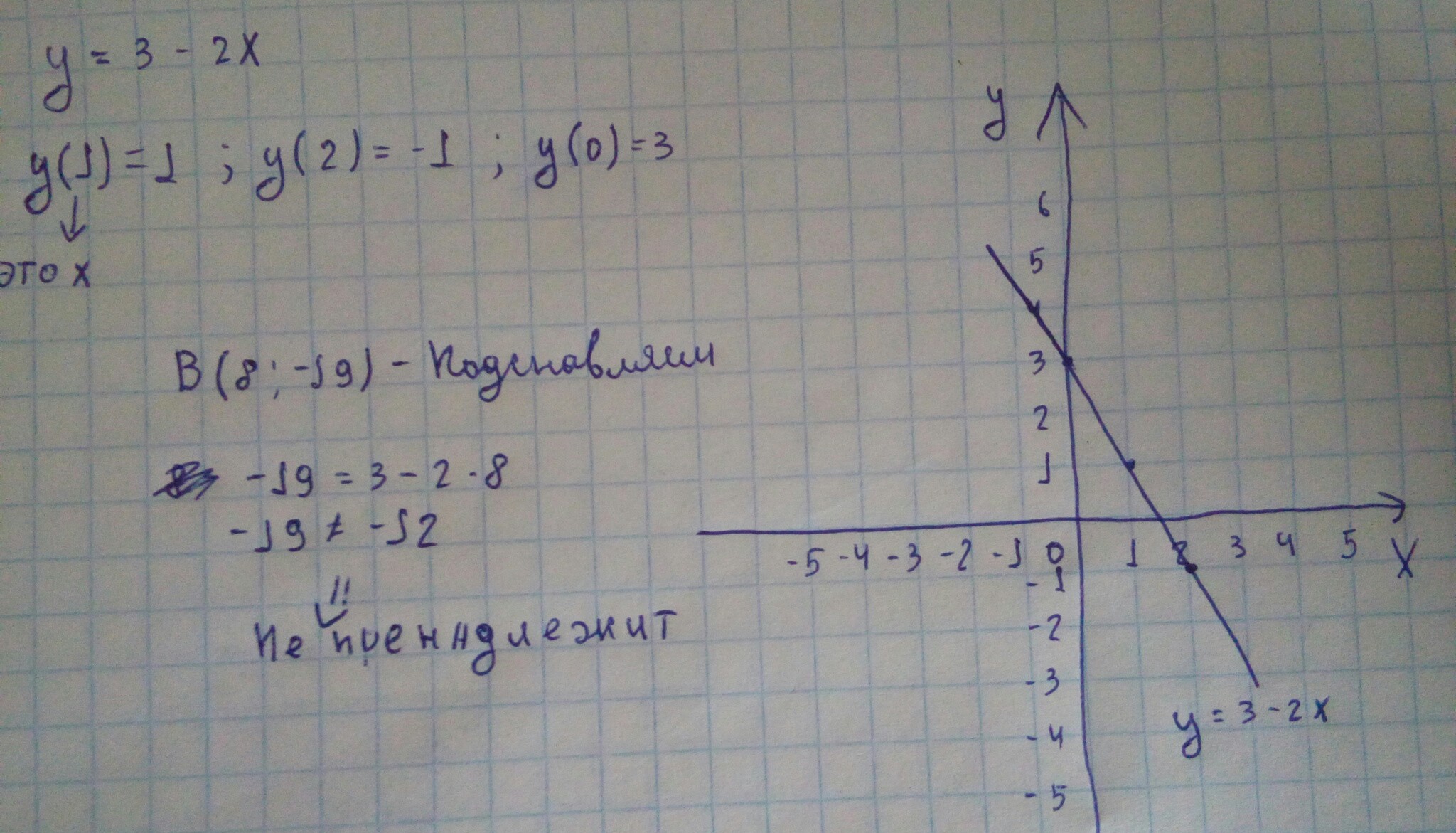
Решить: преобразуйте выражение в многочлен стандартного вида во вложениях 535

б) 2(a-1)^2+3(a-2)^2=2(a^2-2a+1)+3(a^2-4a+4)=2a^2-4a+2+3a^2-12a+12=5a^2-16a+14

в) 5(x-y)^2+(x-2y)^2=5(x^2-2xy+y^2)+x^2-4xy+4y^2=5x^2-10xy+5y^2+x^2-4xy+4y^2=6x^2-14xy+9y^2

г) 4(m-2n)^2-3(3m+n)^2=4(m^2-4mn+4n^2)-3(9m^2+6mn+n^2)=4m^2-16mn+16n^2-27m^2-18mn-3n^2=-23m^2-34mn+13n^2

д) 3(2a-b)^2-5(a-2b)^2=3(4a^2-4ab+b^2)-5(a^2-4ab+4b^2)=12a^2-12ab+3b^2-5a^2+20ab-20b^2=7a^2+8ab-17b^2

e) 4(3x+4y)^2-7(2x-3y)^2=4(9x^2+24xy+16y^2)-7(4x^2-12xy+9y^2)=36x^2+96xy+64y^2-28x^2+84xy-63y^2=8x^2+180xy+y^2

ж) 2(p-3q)^2-4(2p-q)^2-(2q-3p)(p+q)=2(p^2-6pq+9q^2)-4(4p^2-4pq+q^2)-(2pq+2q^2-3p^2-3pq)=2p^2-12pq+18q^2-16p^2+16pq-4q^2-2q^2+3p^2+pq=-11p^2+5pq+12q^2

з) 5(n-5m)^2-6(2n-3m)^2-(3m-n)(7m-n)=5(n^2-10mn+25m^2)-6(4n^2-12mn+9m^2)-(21m^2-3mn-7mn+n^2)=5n^2-50mn+125m^2-24n^2+72mn-54m^2-21m^2+10mn-n^2=-20n^2+32mn+50m^2

и) (x-y)^3=x^3-3x^2*y+3x*y^2-y^3

к) (2a-b)^3=8a^3-12a^2*b+6a*b^2-b^3

Реши

Задание:
Преобразуйте выражение в многочлен стандартного вида.
см. фото

2(p^2+9q^2-6pq)-4(q^2+4p^2-4pq)-2pq-2q^2+3p^2+3pq=
=2p^2+18q^2-12pq-4q^2-16p^2+16pq+pq-2q^2+3p^2=
=-11p^2+12q^2+5pq

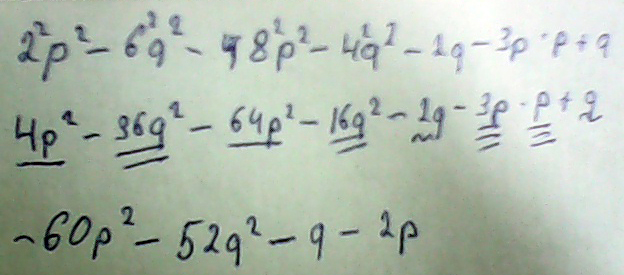
1. Преобразуйте выражение в многочлен стандартного вида: а) (3а - 2) в квадрате б) (2а - 5b)(2a + 5b)
в) (x + 3)(x в квадрате - 3x - 9). Задание 3: Упростите выражение: 3(а+b) в квадрате - (2а + b)(2a - b) Задание 4: Докажите, что число 158 в квадрате - 42 в квадрате кратно 50. Задание 5: Сравните числа (341 + 113) в квадрате и 341 в квадрате + 113 в квадрате. Задание 6: Докажите, что при всех значениях х значение выражения 5 - 6х + 9х в квадрате больше 3. Задание 7: Решите уравнение (3х - 1) в квадрате - (3х + 2)(3х - 2) = 11

1. а)=9а²-12а+4; б)=4а²-25b²; в)=х³+27(эти задание на формулы сокращённого умножения.) задание 3. 3(а+в)²-(2а+в)(2а-в)=3(а²+2ав+в²)-(4а²-в²)=3а²+6ав+3в²-4а²+в²=4в²-а²+6ав. задание 5.(341+113)²= 341²+113²; (341+113)(341+113)= (341+113)(341+113). задание 7. (3х-1)²-(3х+2)(3х-2)=11; 9х²-6х+1-9х²+4=11; -6х=6; х=-1. задание.4. 158²-42²=(158-42)(158+42)=116×200=23200; 23200:50=464

№347 Преобразуйте №347 Преобразуйте выражение в многочлен стандартного вида фото в низу ))№347