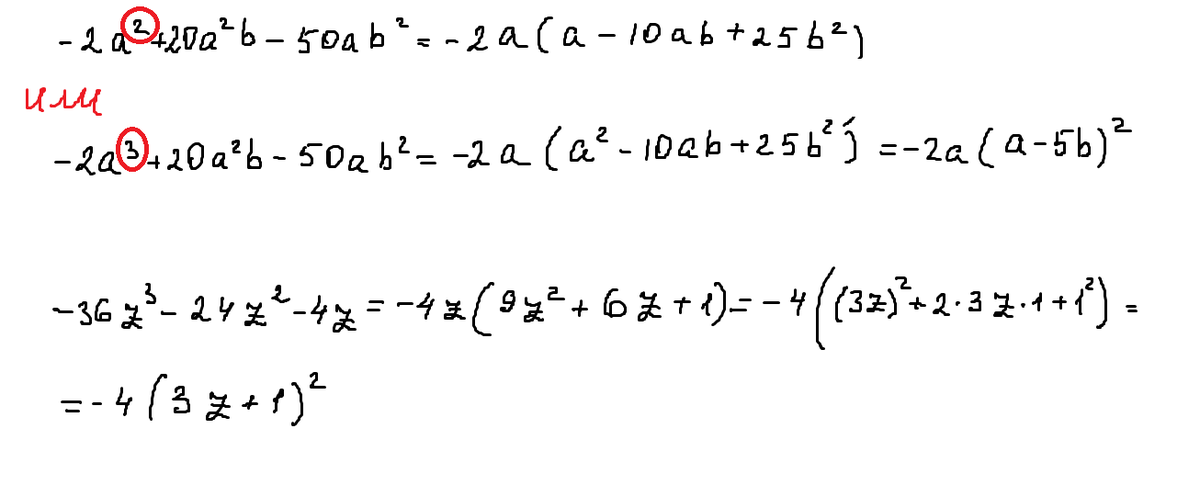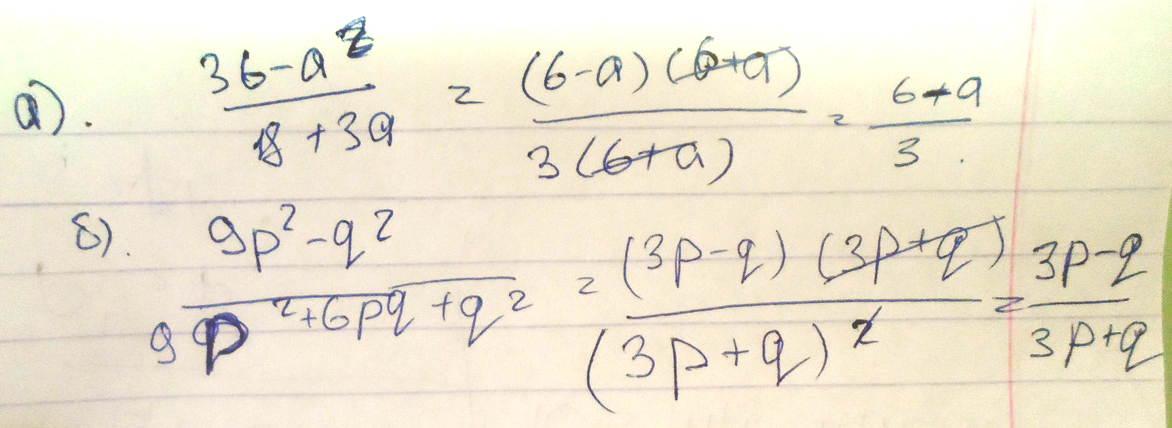многочлен »

разложите многочлен на множители - страница 14

  • Разложите многочлен на множители: 1).2а² + 20а² б - 50аб². 2).36z³ - 24z² -4z.


    Решение: $$ -36z^{3}-24z^{2}-4z=-4z(9z^{2}+6z+1)=-4z(3z+1)^{2}= \\ =-4z(3z+1)(3z+1) $$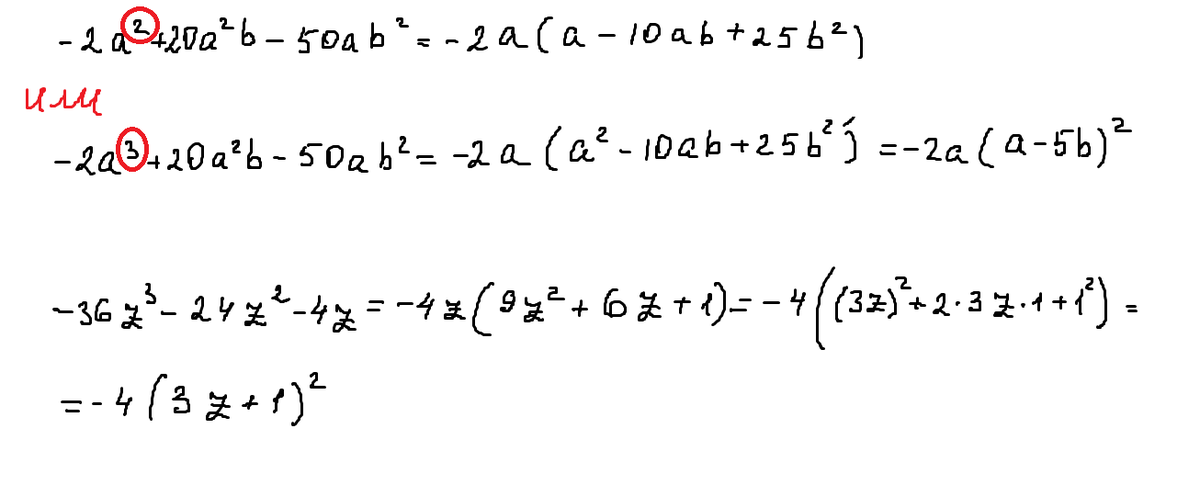- z - z - z - z z z - z z - z z z...

  • Разложите многочлен на множители:
    ^2-число или буква в степени
    1) (p^2-6)-4(p^2-6)^2
    2) 8m(m-3)-3(m-3)^2
    3) (a-4)^3+8a(a-4)
    4) 5x^2(3x-8)+10x(3x-8)^2
    5) 6d^2(2d-5)^2-12d^2(2d^2+5d-25)


    Решение: 1) $$ (p^2-6)-4(p^2-6)^2 = (p^2-6)(1-4p^2+24)= \\ (p^2-6)(25-4p^2)=(p^2-6)(5-2p)(5+2p) $$

    2) $$ 8m(m-3)-3(m-3)^2=(m-3)(8m-3(m-3)) = \\ (m-3)(5m+6) $$

    3) $$ (a-4)^3+8a(a-4) = (a-4)((a-4)^2+8a)= \\ (a-4)(a^2-8a+16+8a)=(a-4)(a^2+16) $$

    4) $$ 5x^2(3x-8)+10x(3x-8)^2 = (3x-8)(5x^2+10x(3x-8))= \\ (3x-8)(5x^2+30x^2-80x)=5x(3x-8)(7x-16) $$

    5) $$ 6d^2(2d-5)^2-12d^2(2d^2+5d-25)= \\ 6d^2(4d^2-20d+25-4d^2-10d+50)=6d^2(-30d+75)= \ 90d^2(5-2d) $$

  • F (х; у)=ух^5у^2х^2 + х^3у^4ху^2 – 2х^4у(-1) у^5– у^3у^3х^4 + 15х^4ух^3у^2+х^2у^2(х^5у – х^2у^4)
    a) Приведите данный многочлен к стандартному виду.
    б) Установите, является ли данный многочлен однородным.
    в) Если данный многочлен является однородным, определите его степень.
    3. Разложите многочлен на множители:


    Решение: Ух^5у^2х^2 + х^3у^4ху^2 – 2х^4у(-1) у^5– у^3у^3х^4 + 15х^4ух^3у^2+х^2у^2(х^5у – х^2у^4)=ух^5у^2х^2 + х^3у^4ху^2 – 2х^4у(-1) у^5– у^3у^3х^4 + 15х^4ух^3у^2+х^2у^2(х^5у – х^2у^4)= х^3у^4ху^2 – 2х^4у(-1) у^5– у^3у^3х^4 + 15х^4ух^3у^2+x^7y^3-x^4y^6= х^3у^4ху^2+2x^4y^6-у^3у^3х^4 + 15х^4ух^3у^2+x^7y^3-x^4y^6 - упростили, теперь приводим к стандартному виду: х^3у^4ху^2+2x^4y^6-у^3у^3х^4 + 15х^4ух^3у^2+x^7y^3-x^4y^6=x^4y^6+16x^7y^3
    a) x^4y^6+16x^7y^3 - стандартный вид 
    б) Данный многочлен однородный
    в) степень равна 10 
    г) x^4*y^3(y^3+16x^3) 

  • 1. Разложите многочлен на множители:
    а) 4х² + 8х
    б) 3m - 6n + mn - 2n²
    в) 9a² - 16
    г) y³ + 18y² + 81y
    2. Сократите дробь:
    а) в числителе 36 - а²
    в знаменателе 18 + 3а
    б) в числителе 9р² - q²
    в знаменателе 9p² + 6pq + q²
    3. Решите уравнение: х³ - 36х =0
    4. Докажите тождество: х² + 14х + 48=(х+8)(х+6)
    :


    Решение: а) 4х вынеси за скобку полу4ится : 4х(х+2)

    б) способ груп-ки м(3+н) -2н(3+н) =(3+н)(м-2н)

    в) разность квадрата 3^2a^2-4^2=(3а-4)(3а+4)

    г) тут вроде только у можно вынести за скобку у(у^2+18y+81) в скобках полу4ился квадрат суммы у(у+9)^2

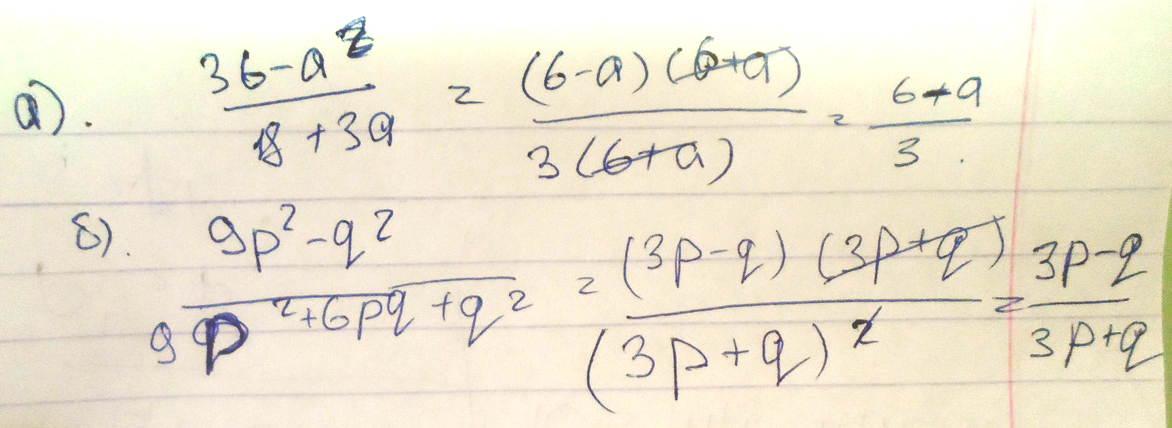
    а х вынеси за скобку полу ится х х б способ груп-ки м н - н н н м- н в разность квадрата a - а- а г тут вроде только у можно вынести за скобку у у y в скобках полу ился квадр...

  • 1. решите уравнение
    (x-4)^2-25=0
    2. вычислите наиболее рациональынм способом
    99^3-61^3
    __________+99*61
    38
    3. докажите тождество
    x^2-12x-45=(x-15)(x+3)
    4.
    Разложите многочлен на множители: а) -12а^2+18a^3 b) 2a+4b-ab-2b^2 v) x^2-64y^2 g) -2x^3-28x^2-98x.
    5. сократите дробь
    a)
    49m^2-n^2
    _______(деление)
    3mn^2-21m^n
    b)
    81x^2-16
    _______(деление)
    16+72x+81x^2
    Решите,


    Решение: 1. X^2-8x+16-25=0

        x^2-8x-9=0

      D=64+36=100

    x1=9

    x2=-1

    5. а) (7m-n)(7m+n)

    разделить на 3mn(n-7m) выносим минус за скобки получается -3mn(7m-n)

    сокращаем (7mn-n) в числителе и знаменателе остается

    (7m+n) разделить на 3mn

<< < 121314