логарифм »
логарифмическое неравенство - страница 2
Решить логарифмические неравенства \( \log_{0,4}\frac{3x+1}{x-2} \geq 1 \\ x^{3\log_2 X+1}\leq 16\)
Решение: 1) ОДЗ
(3x+1)/(x-2)>0
x=-1/3 U x=2
+ _ +
-(-1/3)-(2)-
x<-1/3 U x>2
(3x+1)/(x-2)≤2/5
(15x+5-2x+4)/5(x-2)≤0
(13x+9)/(x-2)≤0
x=-9/13 U x=2
+ _ +
-[-9/13]-(2)-
-9/13≤x<2
x∈[-9/13;-1/3)
2) ОДЗ x>0
прологарифмируем по основанию 2
(3log(2)x+1)*log(2)x≤log(2)16
3log²(2)x+log(2)x≤4
log(2)x=a
3a²+a-4≤0
D=1+48=49
a1=(-1-7)/6=-4/3
a2=(-1+7)/6=1
-4/3≤a≤1
-4/3≤log(2)x≤1
x∈[1/2∛2;2]
Как решать логарифмические неравенства где в левой части logx (f(x))>0
где f(x) функция с х
Решение: При решении неравенства с переменным основанием нужно учитывать, что при основании, большем 1 логарифмическая функция является возрастающей, а при основании от 0 до 1- убывающей. Нужно решить объединение двух систем неравенств. 0=log x (1).
Первая систем{x>1;f(x)>1;f(x)>0} или вторая система {0<x<1;f(x)<1;f(x)>0}. В первой системе неравенство f(x)>0 можно не решать, оно автоматически верно.Решить Логарифмические неравенства 1) \( \log_{\frac{2}{3}}(3x+6) > \log_{\frac{2}{3}}3 + 2\log_{\frac{2}{3}}2 \)
2) \( \log_3(x+20) < 3 \)
Решение:log3(x+20)<3
О. Д. З x+20<0
x<-20
т. к основание больше 1/2 то знак неравенства не меняется.
log3(x+20)
x+20<81
x<61
x<-20 строите интервалы(вы должны проходить это)
Ответ: x<-20
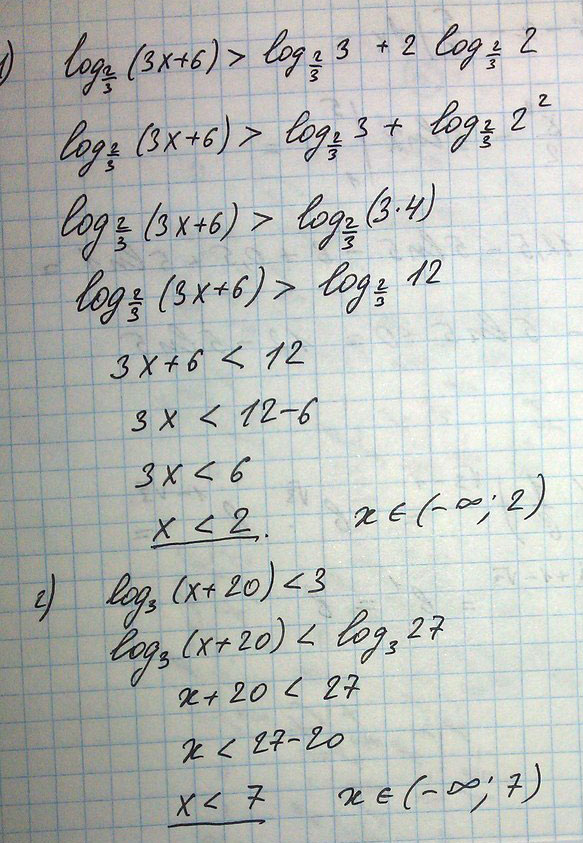
Решите логарифмические неравенства 1. \(\log_2(2x-2) > \log_2(6-5x)\)
2. \( \log_{\frac{1}{2}}(5x-8) > 1\)
3. \(\log_{\pi}\frac{x-2}{x-3} < \log_{\pi}3\)
4. \( \log_{\frac{1}{2}}(2x-2) \geq 0 \)
5. \( \log_4 x+\log_4(x-3) < 1 \)
Решение: 1)2x-2>6-5x ⇒ 7x>8⇒x>8/7 (40/35) (при переходе к неравенству знак сохраняется, т. к. в основании чисто больше 1)
2x-2>0 x>1 (по определению логарифма)
6-5x>0 -5x>-6 ⇒ x<6/5 (42/35) (по определению логарифма)
х∈(8/7;6/5)
2)5х-8<1/2 ⇒ 5x<17/2⇒x<17/10 (знак неравенства меняется т. к. основание меньше 1)
5х-8>0⇒5x>8⇒x>8/5 (16/10)
x∈(8/5;17/10)
4) 2x-2≤1 ⇒ 2x≤3⇒x≤3/2(знак неравенства меняется т. к. основание меньше 1)
2х-2>0 ⇒ x>1
x∈(1;3/2]
5) x(x-3)<4
x²-3x-4<0
(x+1)(x-4)<0 x∈(-1;4)
x>0
x-3>0 ⇒ x>3
ответ: х∈(3;4)
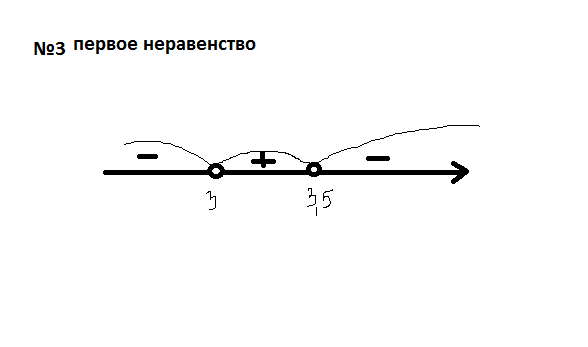
3) (x-2)/(x-3)<3 (т. к. π>1)
(x-2-3x+9)/x-3<0
(-2x+7)/(x-3)<0 x∈(-∞;3)V(3.5;+∞)
x-2/x-3>0
x∈(-∞;2)V(3;+∞)
ответ x∈(-∞;2)V(3,5;+∞)
Решите Простейшие логарифмические неравенства укажите промежуток содержащие все корни уравнения log3(x^2-1)=1 должно получиться [-2;2] 2) 0,8^log0,8(5x-1)=4 должно получиться 1 3) укажите промежуток содержащие все корни уравнения ig(x^2-x+14)=ig(2-9x) в ответе должно быть[-∞;2]
Решение: 1) log3(x^2-1)=log3(3)
x^2-1=3
x=2 или x=-2 оба корня подходят при проверке x^2-1>0
2) 0.8^log0.8(5x-1)=4
5x-1=4
x=1
3) просто отбросьте lg и найдете корни x=-2
x=-6 оба корня подходят при проверке подставляя в x^2-x+14>0 и 2-9x>0 будут соблюдаться одз:x>0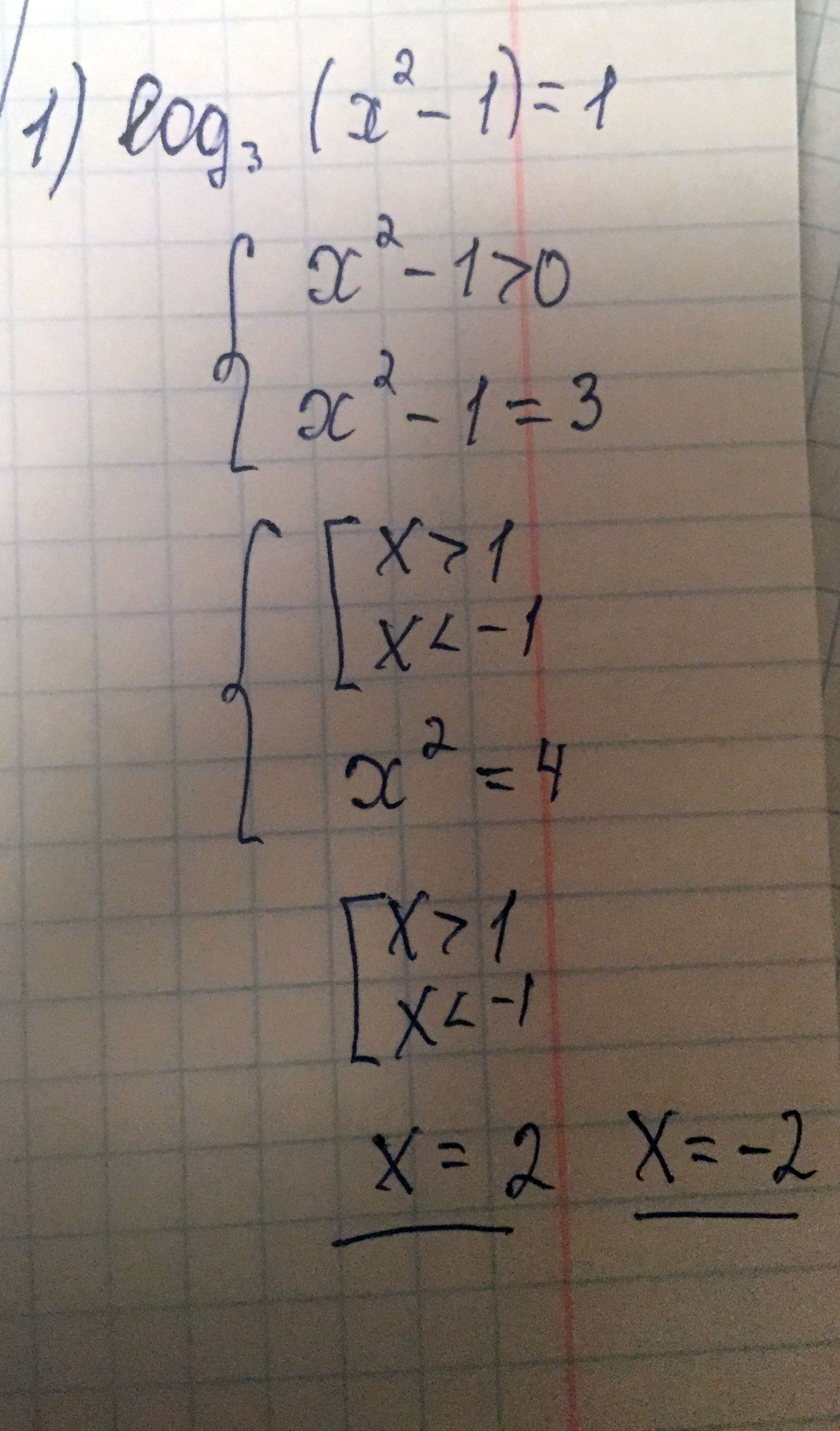


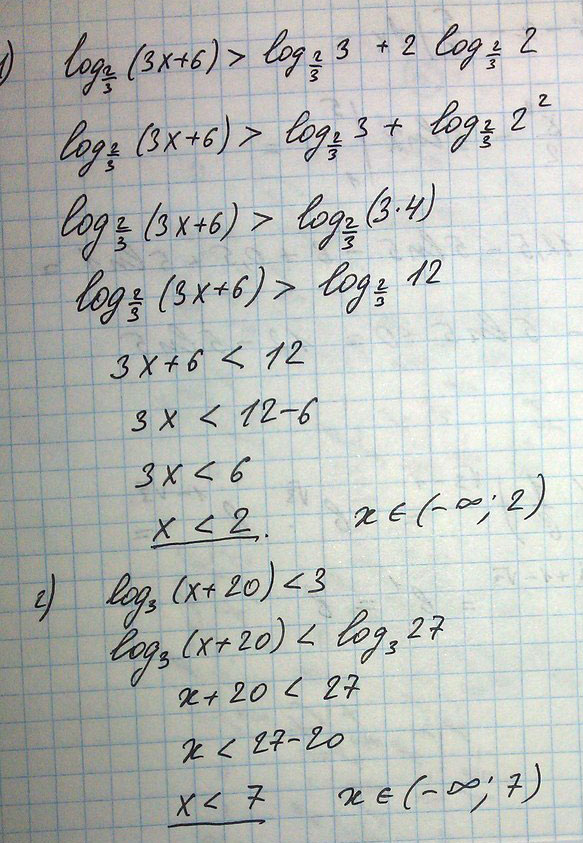

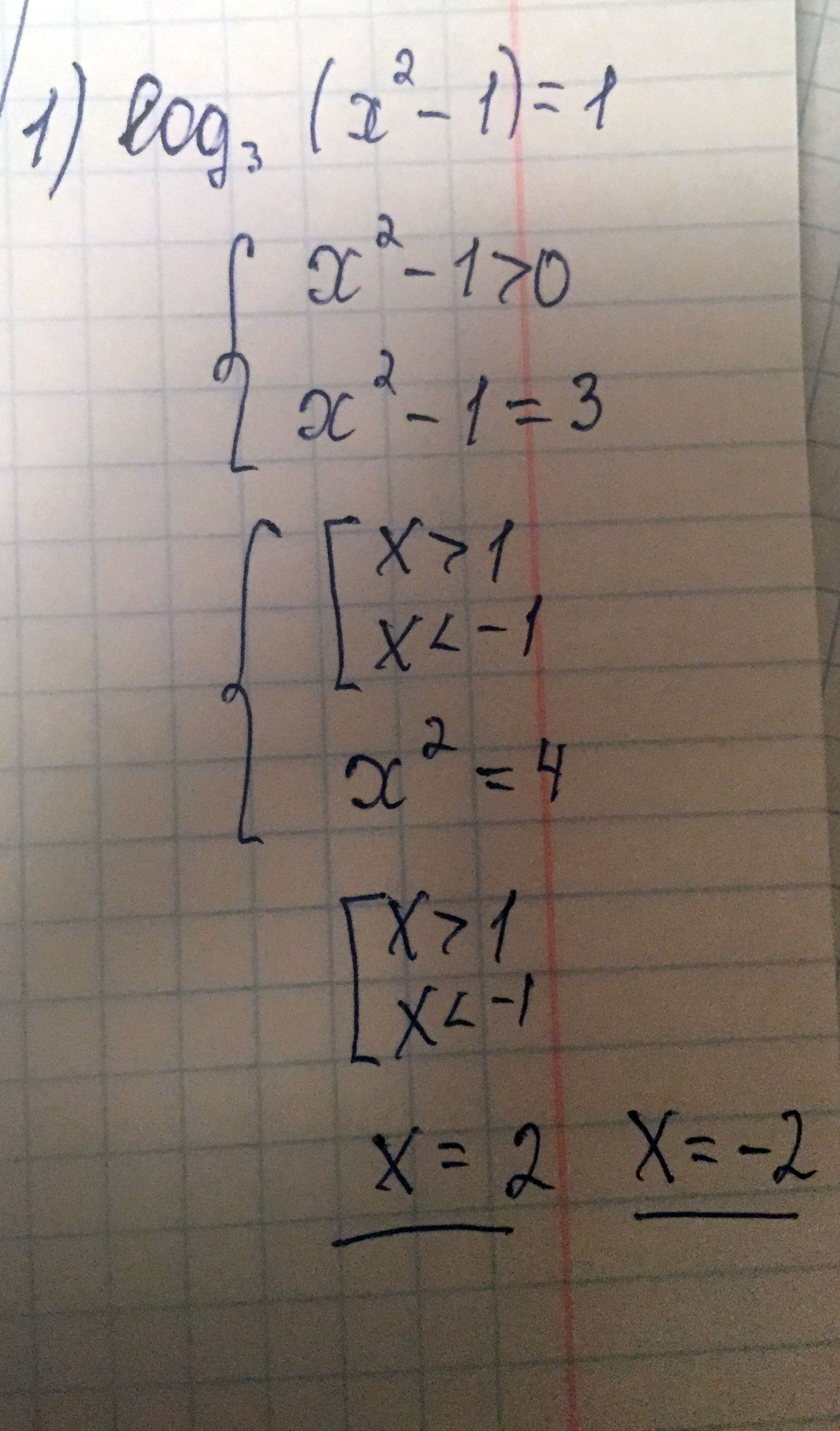
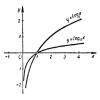 Логарифмической функцией называется функция вида
y = logax,
где а - некоторое фиксированное положительное число, отличное от 1.
Формула y = logax выражает то же самое, что и формула
аy= х. (1)
Отсюда легко установить связь между логарифмической функцией и показательной функцией
у = аx (2)
Если показательная функция (2) описывает изменение степени в зависимости от изменения ее показателя, то ввиду (1) логарифмическая функция, наоборот, описывает изменение...
Логарифмической функцией называется функция вида
y = logax,
где а - некоторое фиксированное положительное число, отличное от 1.
Формула y = logax выражает то же самое, что и формула
аy= х. (1)
Отсюда легко установить связь между логарифмической функцией и показательной функцией
у = аx (2)
Если показательная функция (2) описывает изменение степени в зависимости от изменения ее показателя, то ввиду (1) логарифмическая функция, наоборот, описывает изменение...