логарифм »
логарифмически - страница 2
Уравнение логарифмическое \(\log_3^2(x-2)^3 + 2\log_3(x-2)^2=5\)
Решение: $$ 3log_{3} ^{2} (x-2)+ \ 4log_{3}(x-2) =5 \\ log_{3}(x-2)=t \\ 3t^{2}+4t-5=0 \\ t_{1}=-2 $$ $$ t_{2}=2/3 \\ log_{3}(x-2)=-2 \\ x-2=3^{-2} $$ $$ x=2 \frac{1}{9} \\ log_{3}(x-2)=2/3 \\ x-2=3^{ \frac{2}{3} } $$ $$ x= \sqrt[3]{9} +2 $$
Решить логарифмические неравенства и равенства:
1.lg(x^2-2x)=lg30-1
2.log3(x^2+7x-5)>1
Решение:1
ОДЗ
x(x-2)>0
x=0 x=2
x∈(-∞;0) U (2;∞)
lg(x²-2x)=lg(30/10)
lg(x²-2x)=lg3
x²-2x=3
x²-2x-3=0
x1+x2=2 U x1*x2=-3
x1=-1 U x2=3
2
log(3)(x²+7x-5)>1
{x²+7x-5>0 (1)
{x²+7x-5>3⇒x²+7x-8>0 (2)
1)D=49+20=69
x1=(-7-√69)/2 U x2=(-7+√69)/2
x<(-7-√69)/2 U x>(-7+√69)/2
2)x1+x2=-7 U x1*x2=-8
x1=-8 U x2=1
x<-8 U x>1
x∈(-∞;-8) U (1;∞)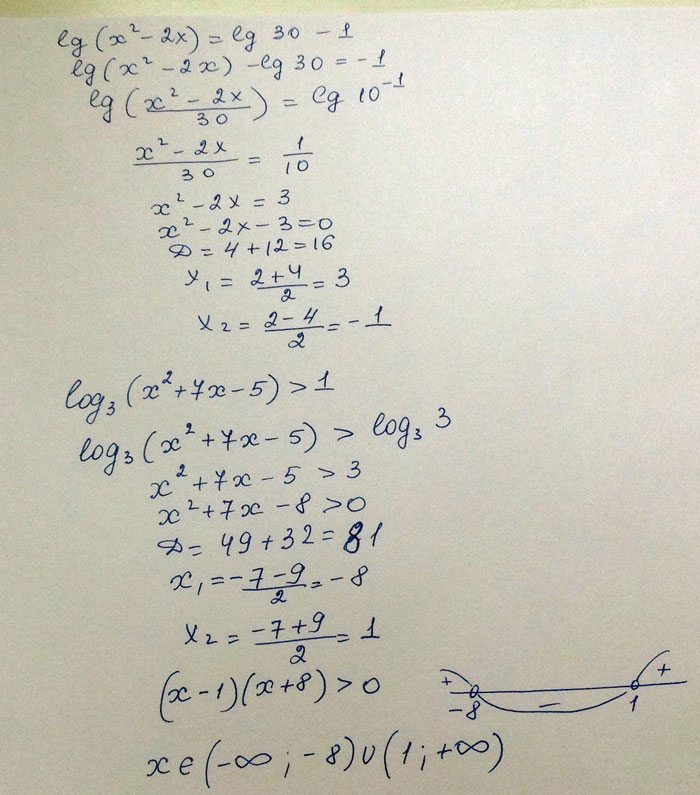
решение логарифмических неравенств: 2log12(√x+5 +1) < log12(x+10); (4x – 1) log2x≥0; 3log8(2x-1) – 2log0,25(x+2)≤0,5log√23
Решение: 2log12(√x+5 +1) < log12(x+10); (4x – 1) log2x≥0; 3log8(2x-1) – 2log0,25(x+2)≤0,5log√23(√x+5 +1)*(√x+5 +1)< x+10
x+5 + 2(√x+5)+1 < x+10
(√x+5 )< 2
x+5 < 4
x< -1
учитывая ОДЗ x> -10, x> -5
(-5; -1)
2) 4x -1=0, x = 0,25
log x = 0, x = 1, x> 0
(0;0,25] [1; до бесконечности)
3) переходик к основанию 2
log2(2x-1) +log2(x+2)≤log2(3)
(2х-1)*(х+2)≤3
2х*х+3х -5 ≤ 0
[-2,5;1] учитывая ОДЗ х > 0,5, x > -2
(0,5;1]
Логарифмическое уравнение \( \lg(x^2-8) =\lg(2-9x) \)
Решение: $$ lg(x^2-8)=lg(2-9x) $$
ОДЗ:
$$ \left \{ {{x^2-8>0^*} \atop {2-9x>0^{**}}} \right. \\\\ *)x^2-8=0\\x=^+_-2\sqrt2\\ **)2-9x>0\\x<4,5 $$
/////+/////(-2√2).(2√2)/////+/////->x
x=0
////////////////////////////////////////////////(4,5).>x
$$ x\in (-\infty;-2\sqrt2)\cup(2\sqrt2;4,5) \\ lg(x^2-8)=lg(2-9x)\\x^2-8=2-9x\\x^2+9x-10=0\\x_{1,2}=\frac{-9^+_-11}{2}\\x_1=-10\ x_2=1 $$
Ответ х=1 не удовлетворяет условию ОДЗ, а значит ответ х=-10логарифмические уравнения решить 1) log₇x =2; 2) log₅x = -3; 3) \(\log_{\frac{1}{8}}(x-4)=-1\) 4) log₂ (x² - 2x) = 0; 5) log₀.₅ (x³ + 1) = -1; 6) log₃.₂(2-x) =log₃.₂(3x+6); 7) log₂(x-6)(x-8) = 3; 8) \( log_{ \sqrt{5} } (4x-6) - log_{ \sqrt{5} } 5 = log_{ \sqrt{5} } (2x-5) \)
Решение: 1) log₇x =2
x=7² = 49
2)log₅x = -3
x = 5⁻³ = 1/125
3) x-4 = \((\frac{1}{8}) ^{-1} =8\)
x = 8+4=12
4) log₂ (x² - 2x) = 0
x² - 2x = 2° =1
x² - 2x - 1=0
D₁ = 2
x₁ = 1+√2
x₂ = 1-√2
5) log₀.₅ (x³ + 1) = -1
x³ + 1 =0.5⁻¹ = 2
x³ = 1
x=1
6) log₃.₂(2-x) =log₃.₂(3x+6)
2-x = 3x+6
-4x = 4
x=-1
7) log₂(x-6)(x-8) = 3
(x-6)(x-8) = 8
x² - 8x - 6x +48=8
x² - 14x + 40=0
D₁ = 49 - 40=9
x₁ = 7+3= 10
x₂ = 7-3 = 4 не удов. т. к x-6>0 и x-8>0
Ответ: 10
8) $$ log_{ \sqrt{5} } (4x-6) - log_{ \sqrt{5} } 5 = log_{ \sqrt{5} } (2x-5) \\ log_{ \sqrt{5} } \frac{4x-6}{5} = log_{ \sqrt{5} } (2x-5) \\ \frac{4x-6}{5} = 2x-5 $$
4x-6 = 10x - 25
-6x = -19 $$x = \frac{19}{6} $$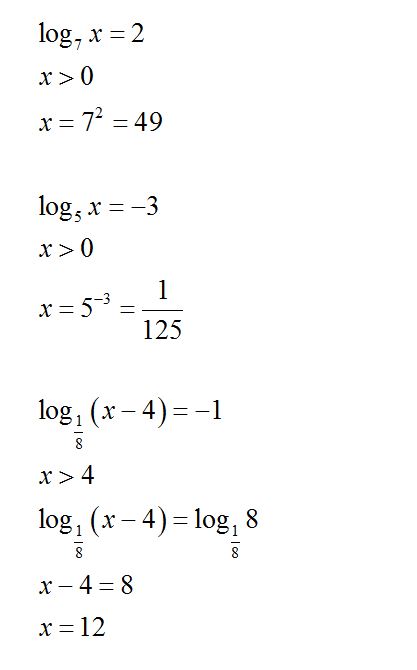

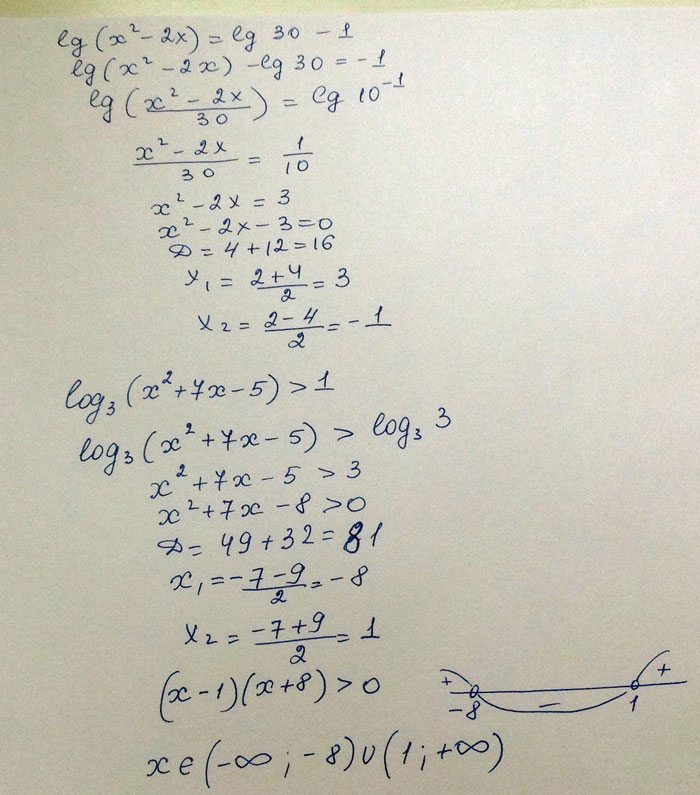
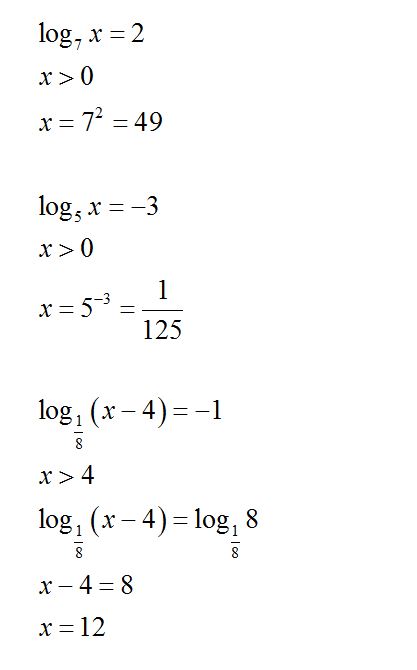
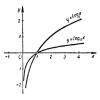 Логарифмической функцией называется функция вида
y = logax,
где а - некоторое фиксированное положительное число, отличное от 1.
Формула y = logax выражает то же самое, что и формула
аy= х. (1)
Отсюда легко установить связь между логарифмической функцией и показательной функцией
у = аx (2)
Если показательная функция (2) описывает изменение степени в зависимости от изменения ее показателя, то ввиду (1) логарифмическая функция, наоборот, описывает изменение...
Логарифмической функцией называется функция вида
y = logax,
где а - некоторое фиксированное положительное число, отличное от 1.
Формула y = logax выражает то же самое, что и формула
аy= х. (1)
Отсюда легко установить связь между логарифмической функцией и показательной функцией
у = аx (2)
Если показательная функция (2) описывает изменение степени в зависимости от изменения ее показателя, то ввиду (1) логарифмическая функция, наоборот, описывает изменение...