логарифм »
логарифмически - страница 4
решить показательное и логарифмическое неравенства \(3\cdot 9^x + 11\cdot 3^x < 4\)
\(\log_3(7-x) > 1\)
Решение: 3*3^(2x)+11*3^x<4
3^x=t
3t+11t-4<0
D=121+24
t1=(-11+13)/6=1/3
t2=(-11-13)/6=-4 Быть не может
3^x=1/3
x=-1
Ответ:x принадлежит от (- бесконечности до -1)
2) log3 (7-x)>1
7-x>3
-x>-4
x<4 ОДЗ: 7-x>0 x<7
Ответ: x принадлежит (от - бесконечности до 4)
3*3^(2x)+11*3^x<4
3^x=t, t>0
3t+11t-4<0
(3t-1)(t+4)<0
+ - +
-(-4)-(1/3)-
t∈(0,1/3)
0<3^x<1/3
x<-1
2) $$ log_3(7-x)\ > \ 1\\7-x\ > \ 0\\x\ < \ 7\\7-x\ > \ 3\\x\ < \ 4\\ Answer: x\ < \ 4 $$
Решите систему логарифмических неравенств \(\begin{cases}\sqrt{4-x^2}(x^2+4x+5) \geq 0\\\log_2(x-3)^2+\log_{0,5}(x^2-9) < 1\end{cases}\)
Решение: $$ \begin{cases}\sqrt{4-x^2}(x^2+4x+5)\geq0^*\\log_2(x-3)^2+log_{0,5}(x^2-9)<1^{**}\end{cases}\\\\ *)\sqrt{4-x^2}(x^2+4x+5)=0\\OD3:\\4-x^2\geq0\\x^2\leq4\\x=^+_-2\\.[-2]///+///[2].>x\\x\in[-2;2]\\\\\sqrt{4-x^2}=0\ \ \ \ \ \ \ \ x^2+4x+5=0\\4-x^2=0\ \ \ \ \ \ \ \ \ \ x_{1,2}=-2^+_-\sqrt{-1}\\x=^+_-2\ \ \ \ \ \ \ \ \ \ \ \ \ \ x\in \varnothing\\.[-2]///+///[2].>x\\OD3:.[-2]///+///[2].>x\\x\in[-2;2] \\ **)log_2(x-3)^2+log_{0,5}(x^2-9)<1\\OD3:\\x^2-9>0\\x^2>9\\x=^+_-3\\///+///(-3).(3)///+///->x\\x\in(-\infty;-3)\cup(3;+\infty)\\log_2(x-3)^2+log_{0,5}(x^2-9)<1\\log_2(x-3)^2-log_{2}(x^2-9)<1\\log_2\frac{(x-3)^2}{x^2-9}<1;2>1\\\frac{(x-3)^2}{x^2-9}<2\\\frac{(x-3)^2-2(x^2-9)}{x^2-9}<0\\\frac{-x^2-6x+27}{x^2-9}<0 \\ x^2+6x-27=0\\x_1=-9\ x_2=3\\\\x^2-9=0\\x=^+_-3\\\\///-///(-9).+.(-3)///-///(3)///-///->x\\OD3:///////+///(-3).(3)///+///->x\\x\in(-\infty;-9)\cup(3;+\infty)\\\\\\.[-2]/////[2].>x\\/////(-9).(3)//////->x $$
Ответ: Решений нетРешение логарифмических неравенств:
1) \( log_{ \frac{1}{3} } ( x+4) > log_{ \frac{1}{3} } ( x^{2}+ 2x-2) \)
2) \( lg( 2x-3) > lg( x+1) \)
3) \( \left \{ {{x-18 \ \ 0} \atop { log_{5}x > 1 }} \right. \)
4) \( \left \{ {{ log_{ \frac{1}{3} }x\ \ -2 } \atop {x+1 > 3}} \right. \)
5) \( \left \{ {{ln x \geq 0} \atop {5-x \ \ 0 }} \right. \)
6) \( \left \{ {{ln x \leq 1} \atop {x+7 > 0}} \right. \)
Решение: $$ 1) \log_{\frac{1}{3}}(x+4) \ > \ \log_{\frac{1}{3}}(x^2+2x-2) \\ x+4 \ < \ x^2+2x-2\\ x^2+2x-2-x-4\ > \ 0\\ x^2+x-6\ > \ 0\\ d=1+24=25\\ x_1=\frac{-1+5}{2}=2; x_2=\frac{-1-5}{2}=-3; $$
Ответ: $$ x \in (2,+\infty) $$ (т. к. отрицательный корень противоречит определению логарифма)
$$ 2) \lg(2x-3) > \lg(x+1) \\ 2x-3 > x+1\\ 2x-x > 1+3\\ x > 4 \\ 3) \left \{ {{x-18 < 0} \atop {\log_5x > 1}} \right. \\ \left \{ {{x < 18} \atop {\log_5x > \log_51}} \right. \\ \left \{ {{x < 18} \atop {x > 1}} \right. \\ x\in(1,18)\\ 4) \left \{ {\log_{\frac{1}{3}}x < -2 \atop {x+1 > 3}} \right.\\ 6) \left \{ {{\ln x \leq 1} \atop {x+7 > 0}} \right. \\ \left \{ {{\ln x \leq \ln0} \atop {x > -7}} \right. \\ \left \{ {{ x \leq 0} \atop {x > -7}} \right. \\ x=0 $$
Т. к. другие значения противоречат определению логарифмаLG(5x-7)>2; log0,1(5-3x)\<-2 решение простейших логарифмических неравенств
Решение: $$ lg(5x-7)\ > \ 2 \\ \\lg(5x-7)\ > \ 2\cdot 1 \\ \\ 1=lg10 \\ \\lg(5x-7)\ > \ 2\cdot lg10 \\ \\lg(5x-7)\ > \ 2\cdot lg10 \\ \\ lg(5x-7)\ > \ lg10^2 \\ \\ \left \{ {{5x-7\ > \ 100} \atop {5x-7\ > \ 0}} \right. \\ \\ 5x\ > \ 107 \\ \\ x\ > \ 21,4 \\ log0,1(5-3x)\ < \ -2 \\ \\ log0,1(5-3x)\ < \ -2\cdot log{0,1}0,1 \\ \\ log0,1(5-3x)\ < \ log{0,1}(0,1)^{-2} \\ \\ \left \{ {{5-3x\ > \ 0} \atop {5-3x\ > \ 100}} \right. \\ \\ 5-3x\ > \ 100 \\ \\ -3x\ > \ 95 \\ \\ x\ < \ -31 \frac{2}{3} $$

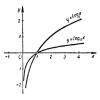 Логарифмической функцией называется функция вида
y = logax,
где а - некоторое фиксированное положительное число, отличное от 1.
Формула y = logax выражает то же самое, что и формула
аy= х. (1)
Отсюда легко установить связь между логарифмической функцией и показательной функцией
у = аx (2)
Если показательная функция (2) описывает изменение степени в зависимости от изменения ее показателя, то ввиду (1) логарифмическая функция, наоборот, описывает изменение...
Логарифмической функцией называется функция вида
y = logax,
где а - некоторое фиксированное положительное число, отличное от 1.
Формула y = logax выражает то же самое, что и формула
аy= х. (1)
Отсюда легко установить связь между логарифмической функцией и показательной функцией
у = аx (2)
Если показательная функция (2) описывает изменение степени в зависимости от изменения ее показателя, то ввиду (1) логарифмическая функция, наоборот, описывает изменение...