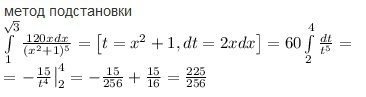интеграл »

определенный интеграл - страница 8

  • Определенный интергал:

    \( \int\limits^1_0 {(2x-1)^{4}} \, dx \)


    Решение: Решаем сначала просто интеграл:
    Интеграл ((2x-1)^4)*dx
    делаем замену t=2x-1 dt=2dx
    интеграл t^4 * dt/2 = 1/2 интеграл t^4= 1/2 ((t^5)/5)= t^5/10
    теперь промежутки: их нужно пересчитать, тк мы поменяли переменную
    t1= 2*0-1= -1
    t2= 2*1-1= 1
    берем интеграл от -1 до 1
    t^5/10
    (1)^5/10 - (-1)^5/10= 1/10 +1/10= 2/10= 1/5

    $$ \bf \int\limits^1_0(2x-1)^4dx=\frac{1}2\int\limits^1_0(2x-1)^4d(2x-1)=\\ \bf =\frac{1}2\frac{(2x-1)^5}5|^1_0=\frac{1}2(\frac{1}5-(-\frac{1}5))=\frac{1}2\frac{2}5=\frac{1}5=0,2 $$

  • Определенный интеграл найти \( \int\limits_1^{\sqrt{3}} \frac{120xdx}{(x^2+1)^5} \)


    Решение: Метод подстановки
    $$ \int\limits_1^{\sqrt{3}} \frac{120xdx}{(x^2+1)^5}=\left[t=x^2+1, dt=2xdx\right]=60\int\limits_2^4 \frac{dt}{t^5}= \\ =\left.\frac{15}{t^4}\right|_2^4=-\frac{15}{256}+\frac{15}{16}=\frac{225}{256} $$

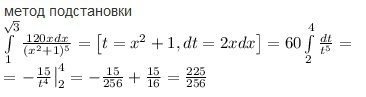
    Метод подстановки int limits sqrt frac xdx x left t x dt xdx right int limits frac dt t left. frac t right - frac frac frac...

  • Решить определенный интеграл \( \int\limits^5_2 { \frac{dx}{(x+1)ln(x+1)} } \)


    Решение: $$ \int\limits^5_2 { \frac{dx}{(x+1)ln(x+1)} } \, = \int\limits^5_2 { \frac{d(ln(x+1)}{ln(x+1)} } \, =ln(ln(x+1) ^{5}_{2} =lnln6-lnln3=ln \frac{ln6}{ln3} \\ \int\limits^{?}_0 {arcsin2x} \, dx= $$
    интеграл считают по частям
    u=arcsin2x  du=(arcsin2x)`dx=1/√(1-4х²) ·(2х)`dx=2dx/√(1-4x²)
    dv=dx  v= x

  • Определенный интеграл dx/(2-sqrt(1+x)), a=0; b=-3/4.


    Решение: Решение:
    Проведем замену:
    $$ t^2 = 1+x $$
    Тогда, dt = d(1+x);
    dt = dx.
    При помощи переменной t решаем уравнение:
    $$ \int \frac{dt}{2-\sqrt{t^2}} = \int \frac{dt}{2-t} = -\int \frac{d(2-t)}{2-t} = -\ln|2-t| + C |t = \sqrt{1+x}| = \\ =-\ln|2-\sqrt{1+x}| + C $$
    Теперь находим определенный интеграл:
    $$ -\ln|2-\sqrt{1+x}| |\int\limits_{-\frac{3}{4}}^0 = -\ln|2-\sqrt{\frac{1}{4}}| + \ln|2-0| = -\ln|2-0.5| +\\ +\ln2 = -\ln1.5 + \ln 2 = \ln2 - \ln1.5 = \ln(\frac{2}{1.5}) = \ln(1\frac{2}{3}) $$

<< < 678