интеграл »
решить интеграл - страница 2
Решить интеграл (с подробным решением )
(3x^2-4x-1)dx
Решение: 1) dx(3x2−4x−1)
2) dx×3x2+dx×−4x−dx
3) 3dxx2+dx×−4x−dx
4) 3dx1+2+dx×−4x−dx
5) 3dx3+dx×−4x−dx
6) 3dx3+−dx×4x−dx
7) 3dx3−dx2×4−dx
8) 3dx3−4dx2−dx
Решение интеграла на фото
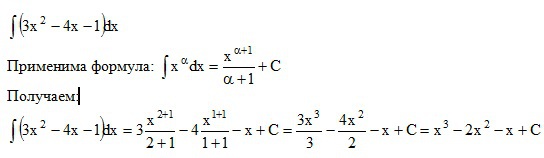
Решить интеграл\( \int\limits { \frac{1}{ \sqrt[3]{x}+ \sqrt[4]{x} } } \, dx \)
Решение: $$ \int\limits{ \frac{1}{ \sqrt[4]{x}+ \sqrt[3]{x} } } \, dx = \int\limits { \frac{12 t^{11} }{ t^{4}+ t^{3} } } \, dx = \int\limits { \frac{12 t^{8} }{ t+ 1 } } \, dx= \\ 12\int\limits { \frac{ (t^{7}- t^{6}+ t^{5} -t^{4} + t^{3} - t^{2} +t-1)(t+1) +1 }{t+1} } \, dx = \\ 12\int\limits{ t^{7}- t^{6}+ t^{5} -t^{4} + t^{3} - t^{2} +t-1 + \frac{1}{t+1} } \, dx = \\ 12( \frac{1}{8} t^{8}- \frac{1}{7} t^{7}+ \frac{1}{6} t^{6} - \frac{1}{5} t^{5} + \frac{1}{4} t^{4} - \frac{1}{3} t^{3} + \frac{1}{2} t^{2} -t + ln(t+1))= \\ 12(\frac{1}{8} x^{ \frac{2}{3} }- \frac{1}{7} x^{ \frac{7}{12} }+ \frac{1}{6} x^{ \frac{1}{2} } - \frac{1}{5} x^{ \frac{5}{12} } + \frac{1}{4} x^{ \frac{1}{3} }{4} + \frac{1}{2} x^{ \frac{1}{6} } - \\ x^{ \frac{1}{12} } +ln(x^{ \frac{1}{12} } +1))= $$
$$ \frac{3}{2} x^{ \frac{2}{3} }- \frac{12}{7} x^{ \frac{7}{12} }+2x^{ \frac{1}{2} } - \frac{12}{5} x^{ \frac{5}{12} } +3 x^{ \frac{1}{3} } - 4 x^{ \frac{1}{4}} + 6 x^{ \frac{1}{6} } - 12 x^{ \frac{1}{12} } + \\ 12ln( x^{ \frac{1}{12} } +1) $$
Решить интеграл
\( 1) \int\limits \frac{dx}{5+9x} \\ \\2) \int\limits ( \sqrt[4]{x}- \frac{2}{ \sqrt[3]{x} }+ x^{4} )dx \\ \\ 3)\int\limits xsin( x^{2} +1)dx \\ \\ 4)\int\limits(3x-8)*sinxdx \\ \\ 5)\int\limits \frac{5x+1}{ x^{2} +7}dx \\ \\ 6)\int\limits x^{2} *sinx \)
Решение: 1)$$ \frac{1}{9} \int\limits { \frac{d(9x+5)}{9x+5} }= \frac{1}{9}ln|9x+5|+C $$
2)$$ \int\limits ({x^{1/4}-2x^{-1/3}+x^4}) \, dx = \frac{x^{(5/4)}}{5/4}- \frac{2x^{(2/3)}}{2/3}+ \frac{x^5}{5}+C $$
3)$$ \frac{1}{2} \int\limits {sin(x^2+1)} \, d(x^2+1)= -cos( x^{2} +1)+C $$
5)$$ \int\limits { \frac{5x}{ x^{2} +7} } \, dx + \int\limits { \frac{dx}{ x^{2} +7} } = \frac{5}{2}ln( x^{2} +7)+ \frac{1}{ \sqrt{7} }arctg \frac{x}{ \sqrt{7} }+C $$
6) по частям: u=x² du=2xdx
dv=sinx v=-cosx
$$ - x^{2} cosx+2 \int\limits {xcosx} \, dx = $$
u=x du=dx
dv=cosx v=sinx
=$$ - x^{2} cosx+xsinx- \int\limits {sinx} \, dx =-x^2cosx+xsinx+cosx+C $$
4)$$ \int\limits {3xsinx} \, dx - \int\limits {8sinx} \, dx =-3xcosx+3 \int\limits {cosx} \, dx +8cosx= $$
=$$ -3xcosx+3sinx+8cosx+C $$Нужно решить интеграл sin(4x)/2sin^2(x)-2+2cos(3x)cos(x) по Dx.
Решение: $$ \int ( \frac{sin4x}{2sin^2x-2} +2cos3x\cdot cosx)dx=\\\\=\int ( \frac{2sin2x\cdot cos2x}{-2(1-sin^2x)} +2\cdot \frac{1}{2}(cos(3x+x)+cos(3x-x))dx=\\\\=\int ( \frac{4sinx\cdot cosx\cdot (2cos^2x-1)}{-2cos^2x} +cos4x+cox2x)dx=\\\\=\int (-4sinx\cdot cosx+2\cdot \frac{sinx}{cosx}+cos4x+cos2x)dx=\\\\=-4\int sinx\cdot d(sinx)+2\int \frac{-d(cosx)}{cosx} +\int cos4x\, dx+\int cos2x\, dx=\\\\=-4\cdot \frac{sin^2x}{2}-2ln|cosx|+\frac{1}{4}sin4x+\frac{1}{2}sin2x+C \\ P.S.\quad d(sinx)=(sinx)’dx=cosx\, dx \\ d(cosx)=(cosx)’dx=-sinx*dx\\\\ \int\limits {cos(ax+b)} \, dx =\frac{1}{a}sin(ax+b)+C $$
Интегал x^4-3x^3+4x^2+6x-8/x^2
Решение: $$ \int\limits { x^4 dx } - 3\int\limits {x^3 dx} + 4\int\limits {x^2 dx} + 6 \int\limits { x dx } - 8 \int\limits {x^{-2} dx} = $$ $$ \frac{x^5}{5} - \frac{3x^4}{4} + \frac{4x^3}{3} + \frac{6x^2}{2} - \frac{8 x^{-1} }{(-1)} = \frac{x^5}{5} - \frac{3x^4}{4} + \frac{4x^3}{3} +3x^2 + \frac{8}{x} $$
1. Применяем правило $$ \int\limits (u+v)dx = \int\limits udx + \int\limits vdx $$ (работает для + и -)
2. Выносим константы за знак интеграла
3. Решаем интегралы ( все табличные ).$$ \frac{1}{x^2} $$ можно (нужно) представить как $$ x^{-2} $$
4. Упрощаем, получаем ответ