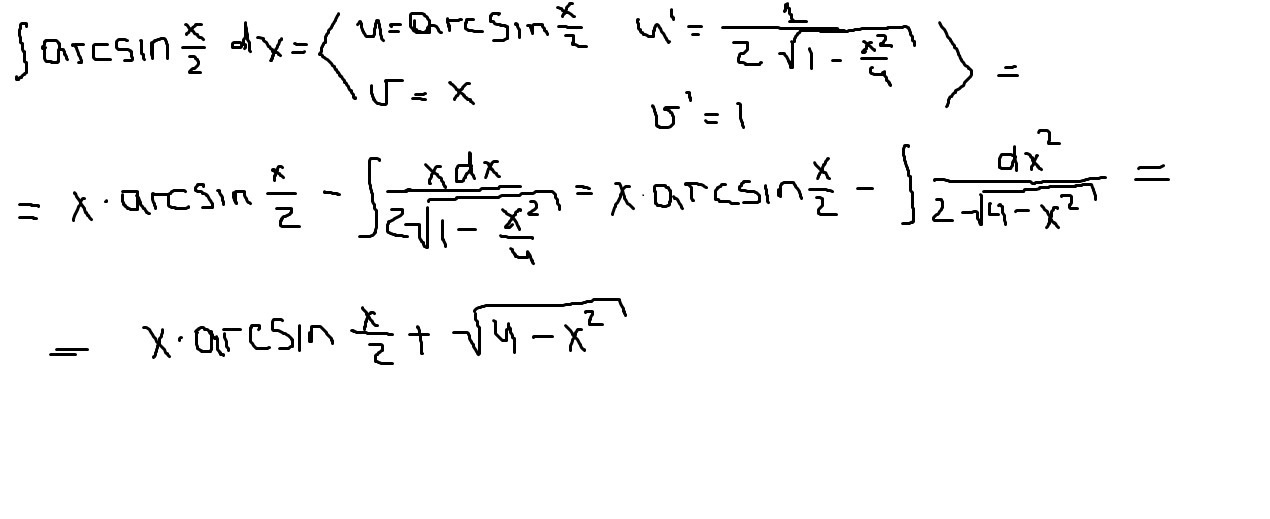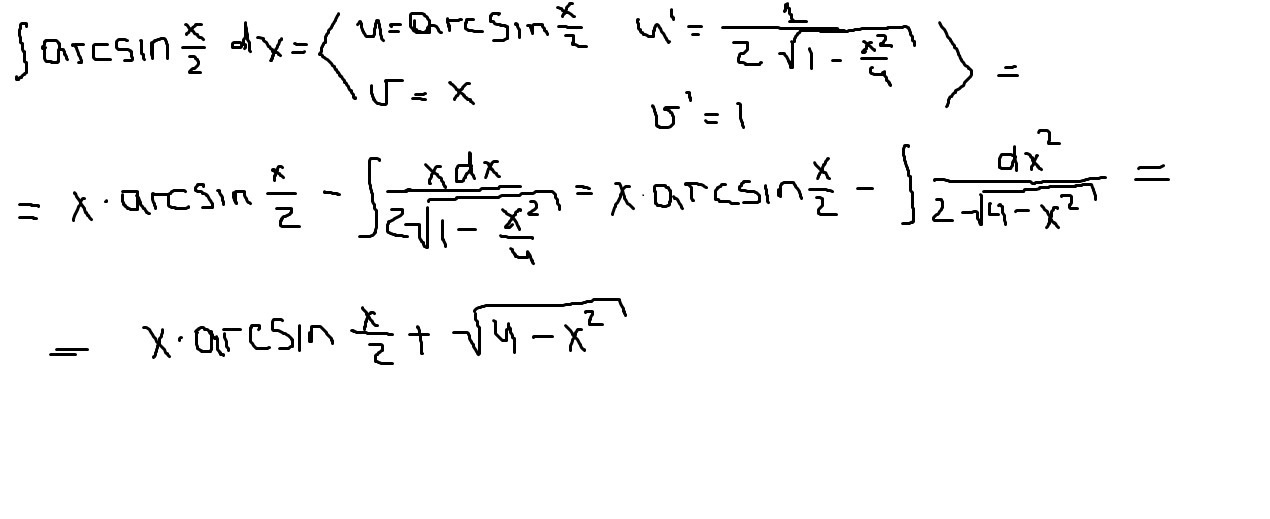интеграл »

решить интеграл - страница 4

  • Решите \( \int\limits{x^2e^{-4x}} \, dx \)


    Решение: $$ \int\limits{x^2e^{-4x}} \, dx $$
    для решения используем метод интегрирования по частям $$ \int\limits{u} \, dv=uv- \int\limits{v} \, du $$ пусть $$ u(x)=x^2 $$ и пусть $$ dv(x)=e^{-4x}dx $$ затем $$ du(x)=2x\,dx $$
    для того чтобы найти $$ v(x) $$ сделаем следующие допущения: пусть $$ u=-4x $$ тогда пусть $$ du=-4dx $$ и подставим $$ -\frac{du}{4} \\ \int\limits{e^u} \, du $$ интеграл от произведения функции на константу есть эта константа на интеграл от данной функции $$ \int\limits{e^u} \, du = - \frac{1}{4} \int\limits{e^u} \, du $$ интеграл от экспоненты есть он же сам $$ \int\limits{e^u} \, du =e^u $$
    таким образом результат будет $$ - \frac{e^u}{4} $$ проведем обратную замену переменной $$ - \frac{1}{4}e^{-4x} $$
    при решении под-интеграла также используем интегрирование по частям по той же схеме, поэтому буду писать только сами действия без пояснений
    интеграл от произведения функции на константу есть константа на интеграл от функции
    $$ \int\limits { \frac{1}{8} e^{-4x}} \, dx= \frac{1}{8} \int\limits{e^{-4x}} \, dx $$
    аналогично проведя те же манипуляции получим
    $$ - \frac{1}{32}e^{-4x} $$
    в итоге получаем следующую функцию
    $$ \frac{x^2}{4}e^{-4x}- \frac{x}{8}e^{-4x}- \frac{1}{32}e^{-4x}+const \\ \\ -\frac{1}{32}(8x^2+4x+1)e^{-4x}+const $$
     

  • При каких значениях x выполняется равенство интеграл с пределами X(больший предел) и 0(меньший предел) (3-2t)dt=4-2x


    Решение: Интеграл(от  0  до  х) (3  -  2t)dt  =  (3t  -  t^2)  (от  0  до  х) = 3х - 3х^2 - 3*0 - 3*0^2 =
                                                     =  3x  -  x^2.
    Полученное  значение  интеграла  приравняем  4  -  2х  и  решим.
    3х  -  x^2  =  4  -  2x
    x^2  -  2x  -  3x  +  4  =  0 
    x^2  -  5 x  +  4  =  0
    По  теореме  Виета  х_1  =  1,  х_2  =  4.
      Ответ.  Равенство  выполняется  при  х_1  =  1,  х_2  =  4

  • Народ Решить интеграл) S-интеграл

    S dx/((x^2+16)*sqrt(9-x^2))


    Решение: integral 1/(sqrt(9-x^2) (x^2+16)) dx
    For the integrand 1/(sqrt(9-x^2) (x^2+16)), Сделаем подстановку x = 3sin(u), тогда  dx = 3cos(u)du. Отсюда sqrt(9-x^2) = sqrt(9-9sin^2(u)) = 3cos(u), u =arcsin(x/3), получаем:
     =  integral du/(9 sin^2(u)+16)
    1/(9 sin^2(u)+16) числитель и знаменатель разделим на cos^2(u):
     integral (du/cos^2(u))/(9 tg^2(u)+16/cos^2(u))
    Т. к. 1/cos^2(u) = tan^2(u)+1:
     integral (du/cos^2(u))/(25tg^2(u)+16)
    Сделаем подстановку s = tg(u) тогда  ds = du/cos^2(u) :
     =  integral ds/(25s^2+16)
     =  integral ds/(16 [(25s^2)/16+1])
    Выносим константу:
     = 1/16 integral ds/[(25s^2)/16+1]
    Подстановка p = (5 s)/4 и  dp = 5/4 ds:
     = 1/20 integral dp/(p^2+1)
    integral ds/(p^2+1) = arctg(p):
     = 1/20 arctg(p)+C
    Возвращаенмся к заменам: для p = (5 s)/4:
     = 1/20 arctg((5 s)/4)+C;
    для s = tg(u):
     = 1/20 arctg((5 tg(u))/4)+C;
    для u = arcsin(x/3):
     1/20 arctg((5 tg(arcsin(x/3)))/4)+C
    tg(arcsin(x/3)=x/(3 sqrt(1-x^2/9))
    Answer:
      = 1/20 arctg((5x)/[4 sqrt(9-x^2)])+C

  • Решить интеграл e^x dx/(e^2x+e^x+1)


    Решение: Замена переменной и выделение полного квадрата
    $$ \int{ \frac{e^x dx}{e^{2x}+e^x+1}}= [e^x=t;d(e^x)=dt]= \int{ \frac{dt}{t^{2}+t+1}}= \int{ \frac{dt}{(t+ \frac{1}{2}) ^{2}} +\frac{3}{4} }= $$
    Формула
    $$ \int{ \frac{dx}{ x^{2} +a ^{2} } }= \frac{1}{a}arctg \frac{x}{a}+C $$
    Получаем
    $$ = \frac{1}{ \sqrt{ \frac{3}{4} } }arctg \frac{t+ \frac{1}{2} }{\sqrt{ \frac{3}{4}} }= \frac{2}{ \sqrt{3} } arctg \frac{2t+1}{ \sqrt{3} }+C= = \frac{2}{ \sqrt{3} } arctg \frac{2 e^{x} +1}{ \sqrt{3} }+C= $$

  • Решить интеграл arcsin(x/2)dx


    Решение: Можете дописать +С, если у вас это требуют ( С - это некоторая константа, на которую отличаются все первообразные данного интеграла )

    Можете дописать С если у вас это требуют С - это некоторая константа на которую отличаются все первообразные данного интеграла...
<< < 234 5 6 > >>