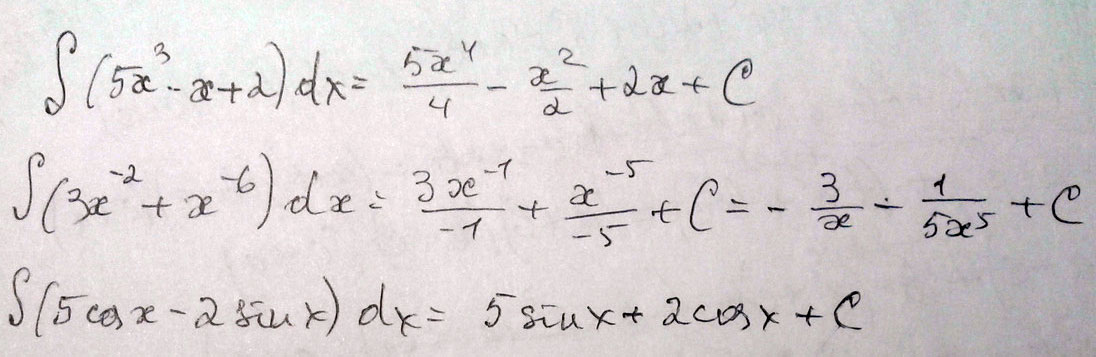интеграл »
решить интеграл - страница 3
Решить интегралы:
(5x^3-x+2) dx
(3x^-2+x^-6)dx
(5cosx-2sinx)dx
Решение: Ищем первообразные.$$ \int\limits {(5x^3-x+2)} \, dx = \frac{5x^4}{4} - \frac{x^2}{2} +2x+C \\ \int\limits {(3x^{-2}+x^{-6})} \, dx = \int\limits {( \frac{3}{x^2} + \frac{1}{x^6})} \, dx = \frac{3x^{-1}}{-1}+ \frac{x^{-5}}{-5} +C =- \frac{15x^4+1}{5x^5} +C \\ \int\limits {(5\cos x-2\sin x)} \, dx =5\sin x+2\cos x+C $$
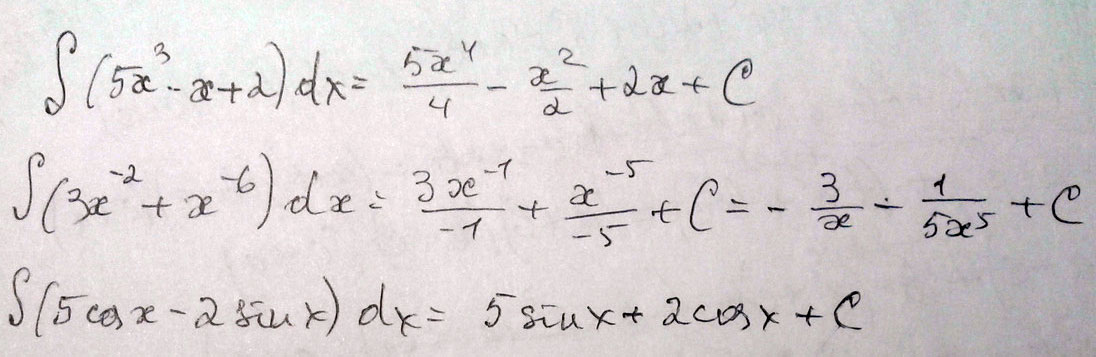
1. Решить системы уравнений методом Гаусса: \( \left \{ {3x-3y+2x=2} \\ {4x-5y+2z=1} \atop {5x-6y+4z=3} \right. \)
2. Решить интеграл методом прямоугольников: \( \int\limits^1_0 { \frac{dx}{1+x} } \, \) при n=5
Решение: $$ 1.\;\left(\begin{array}{ccc|c}3&-3&2&2\\4&-5&2&1\\5&-6&4&3\end{array}\right)=\left(\begin{array}{ccc|c}3&-3&2&2\\0&3&2&5\\0&3&-2&1\end{array}\right)=\\=\left(\begin{array}{ccc|c}3&0&0&3\\0&3&2&5\\0&0&4&4\end{array}\right)=\left(\begin{array}{ccc|c}1&0&0&1\\0&3&0&3\\0&0&1&1\end{array}\right)=\left(\begin{array}{ccc|c}1&0&0&1\\0&1&0&1\\0&0&1&1\end{array}\right)\\\begin{cases}x=1\\y=1\\z=1\end{cases} \\ 2.\;\int\limits_0^1\frac{dx}{1+x},\;n=5\\\Delta x=\frac{b-a}n=\frac{1-0}5=\frac15\\x_k=a+k\cdot\Delta x\\x_0=0+0\cdot\frac15=0\\x_1=0+1\cdot\frac15=\frac15\\x_2=0+2\cdot\frac15=\frac25\\x_3=0+3\cdot\frac15=\frac35\\x_4=0+4\cdot\frac15=\frac45\\f(x_0)=1\\f(x_1)=\frac56\\f(x_2)=\frac57\\f(x_3)=\frac58\\f(x_4)=\frac59 \\ \int\limits_0^1\frac{dx}{1+x}\approx\frac15\cdot\left(1+\frac56+\frac57+\frac58+\frac59\right)=\frac15\cdot\frac{1879}{504}=\frac{1879}{2520} $$
Решить интеграл (Интегральное исчисление функции одной переменной) \( \int \frac{x\cdot cosx}{sin^2x}dx \)
Решение: $$ \int \frac{x\cdot cosx}{sin^2x}dx=[\; u=x\;,\; du=dx\;,dv=\frac{cosx}{sin^2x}dx\;,\; v=-\frac{1}{sinx}\; ]=\\\\=[\; \int u\cdot dv=uv-\int v\cdot du\; ]=\\\\=-\frac{x}{sinx}+\int \frac{dx}{sinx} =- \frac{x}{sinx} +\int \frac{sinx}{sin^2x} dx=- \frac{x}{sinx} +\int \frac{sinx\, dx}{1-cos^2x}=\\\\=- \frac{x}{sinx} -\int \frac{-d(cosx)}{cos^2x-1} =-\frac{x}{sinx}+\frac{1}{2}\cdot ln\left |\frac{cosx-1}{cosx+1}\right |+C=\\\\=-\frac{x}{sinx}+ln\sqrt{\left |\frac{cosx-1}{cosx+1}\right |}+C=-\frac{x}{sinx}+ln|tg\frac{x}{2}|+C \\ P.S.\quad \int \frac{dt}{t^2-1}=\frac{1}{2}\cdot ln\left |\frac{t-1}{t+1}\right |+C\;,\; \; t=cosx $$
Решить интеграл дробно-рациональной функции \( \int\frac{x+1}{x^2 +10x +13}dx \)
Решение: Возьмем производную от знаменателя $$ (x^2+10x+13)’=(x^2)’ + (10x)’ + (13)’ = 2x+10+0=2x+10 $$
В числителе — $$ x+1 \\ \frac{1}{2} (2x+10)=x+5; \ \ \ x+5 -4=x+1 \\ \\ x+1 =\frac{1}{2} \cdot (2x+10)-4=\boxed{\frac{1}{2} d(x^2+10x+13)-4} \\ \int \frac{x+1}{x^2+10x+13}=\int \frac{\frac{1}{2} \cdot d(x^2 +10x+13)-4}{x^2+10x+13}=\\=\int \frac{\frac{1}{2} d(x^2 +10x+13)}{x^2+10x+13} - \int \frac{4}{x^2+10x+13}dx=\\ \\ =\frac{1}{2} \int \frac{ d(x^2 +10x+13)}{x^2+10x+13} - 4\int \frac{dx}{x^2+10x+13} =\frac{1}{2} \cdot \ln{\left| x^2+10x+13 \right|}- \\ \\ -4\int\frac{dx}{(x^2 +2 \cdot 5x+25)-12}=\\=\frac{1}{2} \cdot \ln{\left| x^2+10x+13 \right|}-4\int\frac{dx}{(x+5)^2-(\sqrt{12})^2}= \\ =\frac{1}{2} \cdot \ln{\left| x^2+10x+13 \right|}-4 \cdot \frac{1}{2\sqrt{12}} \cdot \ln{\left| \frac{x+5-\sqrt{12}}{x+5+\sqrt{12}}\right|}+C=\\=\frac{1}{2} \cdot \ln{\left| x^2+10x+13 \right|}-\frac{1}{\sqrt{3}} \cdot \ln{\left| \frac{x+5-\sqrt{12}}{x+5+\sqrt{12}}\right|}+C $$
Формулы, использованные в процессе решения
$$ \int {\frac{dx}{x}} =\ln{\left| x \right|}+C; \ \ \ \int {\frac{dx}{x^2 -a^2}}=\frac{1}{2a}\ln{\left| \frac{x-a}{x+a} \right|}+C $$
Решить интегралы \( 1.\,\, \int\limits^{-1}_{-2} {(-\frac{5}{x^2}+x^2-3x)} \, dx\\ 2.\,\, \int\limits^8_5 {(\frac{2}{(x-2)^2}-\frac{1}{\sqrt{x-4}})} \, dx\\ 3.\,\, \int\limits^2_0 {\frac{x^3-27}{x^2+3x+9}} \, dx\\ 4.\,\, \int\limits^2_1 {\frac{x^3-64}{x^2+4x+16}} \, dx\\ 5.\,\, \int\limits^3_2 {\frac{6x^4-4x^3+7x^2-1}{x^2}} \, dx \)
Решение: $$ 1.\,\, \int\limits^{-1}_{-2} {(-\frac{5}{x^2}+x^2-3x)} \, dx =(\frac{5}x+\frac{x^3}3-\frac{3x^2}2)|^{-1}_{-2}=\\=-5-\frac{1}3-\frac{3}2-(-\frac{5}2-\frac{8}{3}-\frac{3*4}{2})=-\frac{41}6+\frac{67}6=\frac{26}6=\frac{13}3 \\ 2.\,\, \int\limits^8_5 {(\frac{2}{(x-2)^2}-\frac{1}{\sqrt{x-4}})} \, dx =(2*\frac{(x-2)^{-2+1}}{-2+1}-\frac{(x-4)^{-\frac{1}{2+1}}}{-\frac{1}{2+1}})|^8_5= \\ =(-\frac{2}{x-2}-2(x-4)^\frac{1}2)|^8_5=-\frac{2}{6}-2*4^{\frac{1}2}-(-\frac{2}{3}-2*1)=\frac{1}{3}-2=-\frac{5}{3} \\ 3.\,\, \int\limits^2_0 {\frac{x^3-27}{x^2+3x+9}} \, dx =\int\limits^2_0 {\frac{(x-3)(x^2+3x+9)}{x^2+3x+9}} \\ dx=\int\limits^2_0 (x-3) \, dx=\frac{(x-3)^2}{2}|^2_0= \\ =\frac{1}2-\frac{9}2=-\frac{8}2=-4 \\ 4.\,\, \int\limits^2_1 {\frac{x^3-64}{x^2+4x+16}} \, dx =\int\limits^2_1 {\frac{(x-4)(x^2+4x+16)}{x^2+4x+16}} \\ dx=\int\limits^2_1 (x-4) \, dx=\frac{(x-4)^2}{2}|^2_1= \\ =\frac{4}2-\frac{9}2=-\frac{5}2 \\ 5.\,\, \int\limits^3_2 {\frac{6x^4-4x^3+7x^2-1}{x^2}} \, dx =\int\limits^3_2 {(\frac{6x^4}{x^2}-\frac{4x^3}{x^2}+\frac{7x^2}{x^2}-\frac{1}{x^2})} \, dx= \\ =\int\limits^3_2 {(6x^2-4x+7-\frac{1}{x^2})} \, dx =(2x^3-2x^2+7x+\frac{1}x)|^3_2=\\\\=2*27-18+21+\frac{1}3-(16-8+14+\frac{1}2)=\frac{344}6-\frac{135}6=\frac{209}6 $$