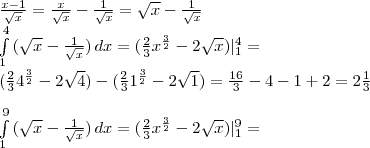интеграл »

решить интеграл - страница 5

  • Решить интеграл \(\int\sqrt{(a^2-x^2)}dx \)


    Решение: интеграл суммы есть сумма интегралов.

    интеграл a^2dx+интеграл-x^2dx

    Проинтегрировали константу:

    a^2x+интеграл-x^2dx

    Вынесли константу из-под знака интеграла

    a^2x-интегралx^2dx

    Проинтегрировали степенную функцию:

    a^2x-1/3x^3

    Записываем финальный ответ:

    знак интеграла a^2-x^2dx=a^2x-1/3x^3+const

  • Нужно решить интеграл простой.
    Здесь а=-1, b=-4 \( \int\limits^a_b {(-4-5x- x^{2} )} \, dx \)


    Решение: Для начала найдём первообразную этой функции
    $$ \int\limits{-x^{2}-5x-4} \, dx =- \int\limits {x^{2}+5x+4} \, dx =-\frac{x^{3}}{3}-5\frac{x^{2}}{2}-4x $$
    По формуле Ньютона-Лейбница найдём значение соответствующего интеграла:
    $$ F(a)-F(b) \\ [-\frac{(-1)^{3}}{3}-5\frac{(-1)^{2}}{2}-4(-1)]-[-\frac{(-4)^{3}}{3}-5\frac{(-4)^{2}}{2}-4(-4)]= \\ \frac{1}{3}-\frac{5}{2}+4-\frac{64}{3}+40-16=-21-2,5+4+40-16=4,5 $$

  • 1) \(\int\limits_1^4(\sqrt{x}-\frac{1}{\sqrt{x}}) dx \\ 2) \int\limits_1^9\frac{x-1}{\sqrt{x}}dx \)


    Решение: $$ \frac{x-1}{ \sqrt{x} }= \frac{x}{ \sqrt{x} } - \frac{1}{ \sqrt{x} } = \sqrt{x} - \frac{1}{ \sqrt{x} } \\ \int\limits^4_1 {( \sqrt{x} }- \frac{1}{ \sqrt{x} }) \, dx =( \frac{2}{3} x^{ \frac{3}{2} }-2 \sqrt{x} )|_{1}^{4}= \\ ( \frac{2}{3} 4^{ \frac{3}{2} }-2 \sqrt{4} ) -( \frac{2}{3} 1^{ \frac{3}{2} }-2 \sqrt{1}) = \frac{16}{3} -4-1+2=2 \frac{1}{3} \\ \int\limits^9_1 {( \sqrt{x} }- \frac{1}{ \sqrt{x} }) \, dx =( \frac{2}{3} x^{ \frac{3}{2} }-2 \sqrt{x} )|_{1}^{9}= \\ \\ ( \frac{2}{3} 9^{ \frac{3}{2} }-2 \sqrt{9} )-( \frac{2}{3} 1^{ \frac{3}{2} }-2 \sqrt{1} )=(18-6)-(1-2)=12-1+2=13 \\ $$

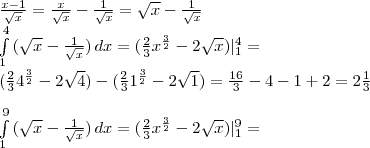
    frac x- sqrt x frac x sqrt x - frac sqrt x sqrt x - frac sqrt x int limits sqrt x - frac sqrt x dx frac x frac - sqrt x frac frac - sqrt - frac frac - sqrt frac - - frac int...

  • решить интеграл 1/3 интеграл (d(1+x^3))/(1+x^3)


    Решение: 1/3 интеграл (d(1+x^3))/(1+x^3)=1/3ln модуль(1+x^3)+c

    Занесем х^2 из числиться под знак дифференциала. после этого нам нужно компенсировать то что получится от взятия дифференциала от х^3, это 3х^2dx. Значит нам не хватает 1/3. Получим:
    интеграл((dx^3)/(x^3+1))
    теперь прибавим 1 под знаком дифференциала:
    интеграл((d(x^3+1))/(x^3+1))
    теперь посчитаем:
    ln(x^3+1)+C
    что непонятно спрашивай в личку

  • нужно решить интеграл cos7x*sin8x


    Решение: Перепишем выражение
    $$ cos(7x)sin(8x)= \frac{1}{2}sin(15x)+ \frac{1}{2}sin(x) \\ \int\limits \frac{1}{2}sin(15x)+ \frac{1}{2}sin(x) \, dx $$
    интеграл суммы есть сумма интегралов
    $$ \int\limits \frac{1}{2}sin {15x}\,dx+ \int\limits \frac{1}{2} sin{x} \, dx $$
    в первом и во втором интегралах вынесем константы за знак интеграла
    $$ \frac{1}{2} \int\limits sin {15x} \, dx + \frac{1}{2} \int\limits sin{x} \, dx $$
    в первом интеграле произведем замену переменной u=15x
    $$ \frac{1}{2} \int\limits \frac{1}{15}sin {u} \, du + \frac{1}{2} \int\limits sin{x} \, dx $$
    проинтегрируем первый синус
    $$ - \frac{1}{30}cos(u)+ \frac{1}{2} \int\limits {sin x} \, dx $$
    проведем обратную замену переменной
    $$ - \frac{1}{30}cos(15x)+ \frac{1}{2} \int\limits sin{x} \, dx $$
    и проинтегрируем второй синус
    $$ - \frac{1}{30}cos(15x)- \frac{1}{2}cos(x) $$

<< < 345 6 7 > >>