интеграл »

найдите площадь фигуры, ограниченной графиком функции

  • Найдите площадь фигуры, ограниченной линиями: \( y=\frac{16}{x^2}, \\ y=2x, \\ x=4. \)


    Решение: ...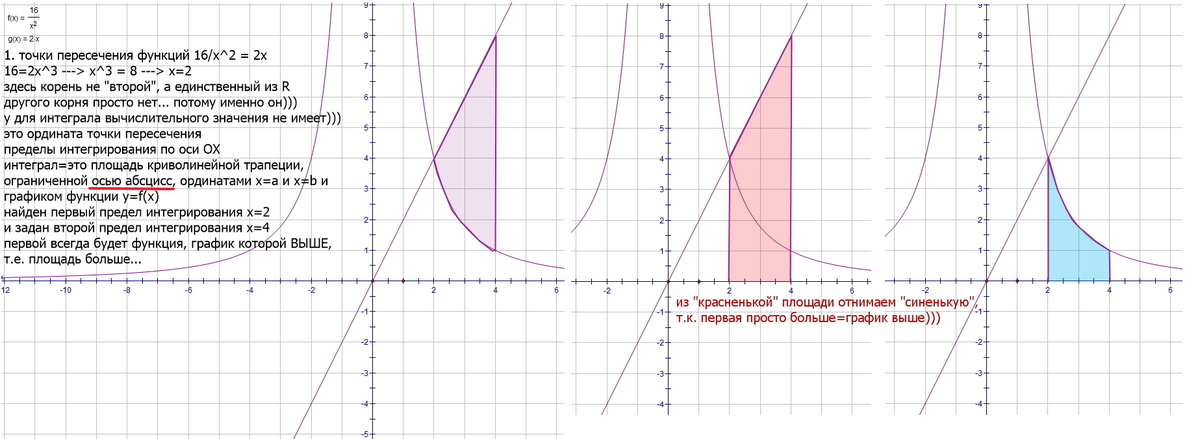

  • 1. Найдите ту первообразную F(x) для функции f(x)=4x^3-8x, график которой проходит через точку А(1;3)

    2. Вычислите площадь фигуры, ограниченной линиями у=х^2 и у=4


    Решение: $$ 1) f(x) = 4x^3 - 8x; A(1;3)\\ F(x) = 4*\frac{x^4}{4} - 8*\frac{x^2}{2} + C = x^4 - 4x^2 + C $$

    У нас есть некоторая неопределенная первообразная, о чем нам говорит число С, его нам и надо найти, найдя его, найдем единственно нужную нам первообразную.

    на даны координаты точки A(1;3) - 1 - x, 3 - y.

    поэтому подставляем 3-ойку вместо значения функции, а единицу вместо значения x.

    $$ F(x)=x^4 - 4x^2 + C\\ 3 = 1^4 - 4*1^2 + C\\ 3 = 1 - 4 +C\\ 3 = -3 + C\\ C = 6\\ $$

    поставляем это значение в первообразную

    $$ F(x)=x^4 - 4x^2 + C\\ F(x) = x^4 - 4x^2 + 6 $$

    Это и есть ответ.

    2)площадь этой фигуры находится как интеграл от разности графиков y=4 и у=х^2, при чем ограничивается этот интеграл точками пересечениями этих графиков.

    x^2 = 4

    x = 2; - 2

    $$ S_= \int_{-2}^{2} {(4-x^2)} \, dx = (4x - \frac{x^3}{3})| =\\ = (8 - \frac{8}{3}) - (-8 - \frac{-8}{3}) = 10\frac{2}{3} $$

  • №1. вычислите интеграл \( \int\limits^1_-1{(3 x^{2} -7x+5)dx} \, \) (нижний предел -1)
    №2. Для функции f(x)=4x+\( \frac{1}{x^{2} } \) найдите первообразную график которой проходит через точку M(-1:4)
    №3. вычислите (предварительно сделав рисунок) площадь фигуры ограниченной линиями
    y=\( x^{2} \)-4x+5, у=0,x=0.x=4


    Решение: 1)
    $$ \int\limits^1_{-1} {(3x^2-7x+5)} \, dx =(x^3- \frac{7}{2}x^2+5x)|^1_{-1}= \\ =1- \frac{7}{2} +5+1+ \frac{7}{2} +5=12. $$
    2)
    $$ F(x)=2x^2- \frac{1}{x} +C $$
    F(-1) = 4   =>  2+1+C=4    => C=1.
    Итак, $$ F(x) = 2x^2- \frac{1}{x} +1. $$
    3) Рисунок во вложении 
    $$ S_{OABC}=\int\limits^4_{0} {(x^2-4x+5)} \, dx =( \frac{x^3}{3} -2x^2+5x)|^4_0= \\ = \frac{64}{3} -32+20=9 \frac{1}{3} $$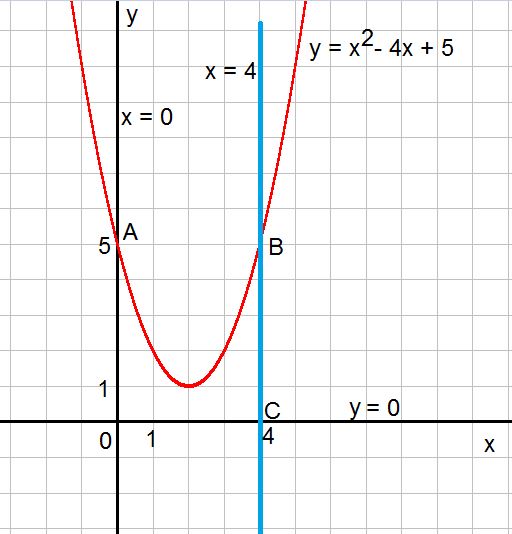

    int limits - x - x dx x - frac x x - - frac frac . F x x - frac x C F -          C     C .Итак   F x x - frac x .  Рисунок во вложении  S OABC int limits x - x dx frac x - x...

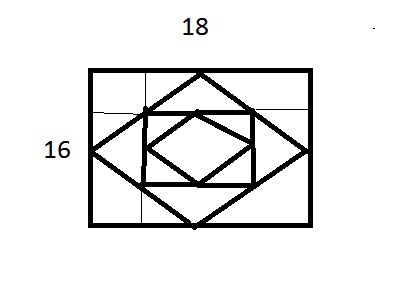
  • В прямоугольник со сторонами 16см и 18см вписывается ромб, вершины которого являются серединами сторон прямоугольника. В полученный ромб аналогичным образом вписывается прямоугольник, а в него снова ромб и так далее. Докажите, что площади полученных фигур образуют геометрическую прогрессию. Найдите знаменатель этой прогрессии


    Решение: S₁(данного прямоугольника)=a·b=18·16;
    S₂(ромба вписанного в данный прямоугольник)=(1/2)·D₁·D₂=(1/2)·16·18;
    S₃=(a/2)(b/2)=(18·16)/4;
    S₄=(1/2)·d₁·d₂=(1/2)·(16/2)·(18/2)=(16·18)/8;
    q=S₄:S₃=S₃:S₂=S₂:S₁=1/2.
    О т в е т. q=1/2.

    S данного прямоугольника a b S ромба вписанного в данный прямоугольник D D S a b S d d q S S S S S S .О т в е т. q ....

  • Найдите площадь фигуры, ограниченной линией
    модуль их Х + модуль из У=6


    Решение: |x|+|y|=6, график так заданной функции будет квадрат с вершинами (6;0)(0;6)(-6;0)(0;-6), что легко установить построив графики данной функции во всех 4 четвертях (квадрантах)
    а площадь такого квадрата можно найти из того, что диагональ равна 12
    , ну например из теоремы Пифагора следует, что квадрат диагонали квадрата равен удвоенному квадрату стороны, а значит удвоенный квадрат стороны(площадь) равна половине квадрата диагонали
    площадь равна 12*12/2=12*6=72 
    Ответ:72 квадратных единицы

1 2 3 > >>