интеграл »

найдите площадь фигуры, ограниченной графиком функции - страница 2

  • Тема: Вычисление площадей плоских фигур с помощью определенного интеграла.
    Пример 1
    2x-3y+6=0 y=0 ; x=3
    Пример 2
    y=-x^2+6x-5 y=0 ; x=2 ; x=3


    Решение: 1. 2x-3y+6=0
    3y = 2x+6
    y = 2/3x+2
    Точка пересечения графиков (приравниваем функции).
    2/3x+2 = 0
    2/3x = -2
    x = -3
    M(-3; 0)
    Фигура сверху ограничена прямой y = 2/3x+2, снизу прямой y=0, слева точкой x=-3, справа прямой x=3.
    $$ \int_{-3}^3(\frac23x+2-0)dx=\int_{-3}^3(\frac23x+2)dx=\left.(\frac13x^2+2x)\right|_{-3}^3=\\=\frac13(3)^2+2\cdot3-\frac13(-3)^2-2(-3)=\frac93+6-\frac93+6=12 $$
    2. Сверху фигура ограничена параболой y=-x^2+6x-5, снизу прямой y=0, слева и справа прямыми x=2 и x=3 соответственно.
    $$ \int_2^3(-x^2+6x-5-0)dx=\int_2^3(-x^2+6x-5)dx=\\=\left.(-\frac13x^3+3x^2-5x)\right|_2^3=-\frac{(3)^3}3+3(3)^2-5\cdot3+\frac{(2)^3}3-3(2)^2+5\cdot2=\\=-9+27-15+\frac83-12+10=1+\frac83=1+2\frac23=3\frac23 $$
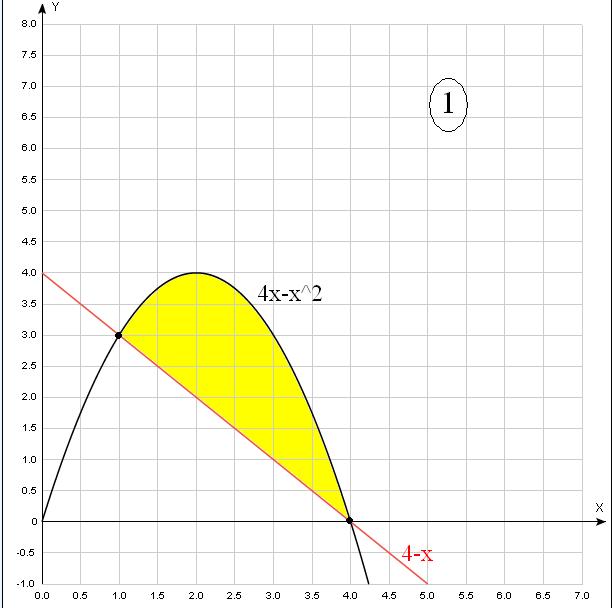
    Решается просто: сначала нарисуйте заданные линии (можно схематически), затем определите левую и правую границы (они либо заданы, как в примере 2, либо находятся, как точки пересечения графиков). Эти границы будут пределами интегрирования. Под знаком интеграла вычитаем из "верхней" (график которой выше) функции "нижнюю" (график которой ниже).

  • Вычислите площадь фигуры, ограниченной линиями: а) y=4x-x^2; e=4-x; б) y=x^2, y=2x; в) y=x^2-4x+4, y=4-x^2; г) y=x^2 -2x+2, y=2+6x-x^2;


    Решение: 1) пределы интегрирования:
    $$ 4x-x^{2}=4-x \\ 4x-x^{2}-4+x=0 \\ x^{2}-5x+4=0, D=25-16=9>0 \\ x_{1}= \frac{5-3}{2}=1 \\ x_{2}= \frac{5+3}{2}=4 \\ S= \int\limits^4_1 {(4x-x^{2}-4+x)} \\, dx= \int\limits^4_1 {(5x-x^{2}-4)} \\, dx= \frac{5x^{2}}{2}-\frac{x^{3}}{3}-4x=\frac{5*4^{2}}{2}-\frac{4^{3}}{3}-4*4-(\frac{5}{2}-\frac{1}{3}-4)=\\=40-\frac{64}{3}-16-\frac{5}{2}+\frac{1}{3}+4=28-\frac{63}{3}-\frac{5}{2}=\\=28-\frac{63*2+15}{6}=28-23.5=4.5 $$
    2) $$ x^{2}=2x \\ x*(x-2)=0 \\ x_{1}=0, x_{2}=2 \\ S= \int\limits^2_0 {(2x-x^{2})} \, dx=\\= x^{2}-\frac{x^{3}}{3}=2^{2}-\frac{2^{3}}{3}=\frac{12-8}{3}=\\=\frac{4}{3} $$
    3) $$ x^{2}-4x+4=4-x^{2} \\ 2x^{2}-4x=0 \\ 2x*(x-2)=0 \\ x_{1}=0, x_{2}=2 \\ S= \int\limits^2_0 {(4-x^{2}-x^{2}+4x-4)} \, dx=\int\limits^2_0 {(-2x^{2}+4x)} \, dx= -\frac{2x^{3}}{3}+2x^{2}=\\=-\frac{2*2^{3}}{3}+2*2^{2}=8-\frac{16}{3}=\\=\frac{24-16}{3}=\frac{8}{3} $$
    4) $$ x^{2}-2x+2=2+6x-x^{2} \\ 2x^{2}-8x=0 \\ 2x*(x-4)=0 \\ x_{1}=0, x_{2}=4 \\ S= \int\limits^4_0 {(2+6x-x^{2}-x^{2}+2x-2)} \\, dx=\int\limits^4_0 {(8x-2x^{2})} \\, dx=4x^{2}- \frac{2x^{3}}{3}=4*4^{2}-\frac{2*4^{3}}{3}=\\=64-\frac{64*2}{3}=\frac{64*3-64*2}{3}=\frac{64*(3-2)}{3}=\frac{64}{3} $$
    Желтым закрашена искомая площадь

    пределы интегрирования x-x -x x-x - x x - x D - x frac - x frac S int limits x-x - x dx int limits x-x - dx frac x - frac x - x frac - frac - - frac - frac - - frac - - frac...

  • найти площадь фигуры ограниченной функциями у=х^2,y=2x. через интеграл нужно решить


    Решение: Построим график. Будет видно, что площадь надо искать на промежутке [0;2]. В данном случае 

    f(x) = 2x

    g(x) = x^2

    Площадь данной фигуры находим по формуле

    S = $$ \int\limits^b_a {(f(x) - g(x))} \, dx $$

    Теперь подставляем и находим

    S = $$ \int\limits^2_0 {(2x - x^2)} \, dx = \frac{2x^2}{2} - \frac{x^3}{3} = x^2 - \frac{x^3}{3} = 2^2 - \frac{2^3}{3} = 4 - \frac{8}{3} = 1\frac{1}{3} $$ ед^2

  • Запишите интеграл, с помощью которого можно найти объем тела, полученного вращением вокруг оси Оу криволинейной трапеции, ограниченной дугой АВ гиперболы у=6/(х-1)-1, если А(0,5), В(5,0)


    Решение: Рассмотрим точку В(5;0). При х=5 у=6/(5-1)-1=1,5-1=0,5. То есть криволинейная трапеция ограничена линиями х=0, y=5 (точка А), у=0,5 (точка В) и y=6/(x-1)-1.
    Для нахождения объёма тела вращения вокруг оси ОY необходимо перейти к обратной функции, грубо говоря нужно выразить "икс" через "игрек":
    y=6/(x-1)-1=(6-(x-1))/(x-1)=(7-x)/(x-1)
    y(x-1)=7-x
    yx-y-7+x=0
    x(y+1)=7+y
    x=(7+y)/(y+1)=6/(y+1)+1
    Теперь подставляем в формулу объема для тела полученного вращением 
    $$ V= \pi \int\limits^a_b {f^2(x)} \, dx $$
    В данном случае 
    $$ V= \pi \int\limits^5_ \frac{1}{2} {( \frac{6}{y+1)}+1)^2 } \, dx $$

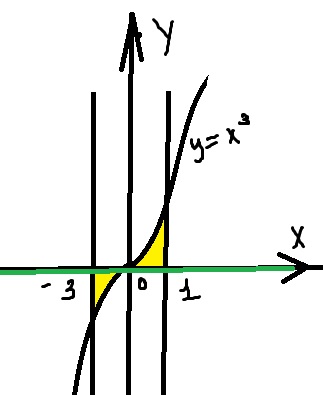
  • Задание найдите площадь фигуры ограниченной линиями у=х^3 y=0 x= -3 x=1 площадь нужно найти через интеграл


    Решение: Здесь разбивается на 2 интеграла 
    И сумма будет положительный
    Нижний интеграл брать с минусом не надо, его просто складывают с верхним 
    См. рисунок

    S =S₁+S₂= интеграл (0 - x³)dx + интеграл (x³ -0)dx = 
      a₁ = - 3, b₁ =0 a₂ = 0, b2 =1  
    -(x^4)/4 | a₁ = - 3, b₁ =0  +(x^4)/4 | a₂ = 0, b2 =1 = -((0^4)/4 -((-3)^4)/4) +(1^4)/4 -(0^4)/4 =
    =81/4 +1/4 =82/4 =20,5.
    * * * интеграл f(x)dx =F(x) | a ->b =F(b) - F(a) * * *
      a ->b

    Здесь разбивается на интеграла И сумма будет положительныйНижний интеграл брать с минусом не надо его просто складывают с верхним См. рисунок S S S интеграл - x dx  интеграл...
<< < 12 3 4 > >>