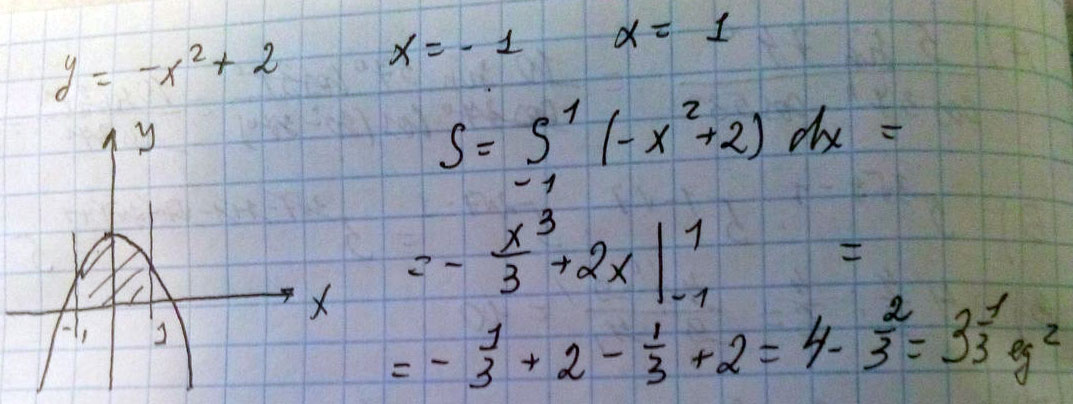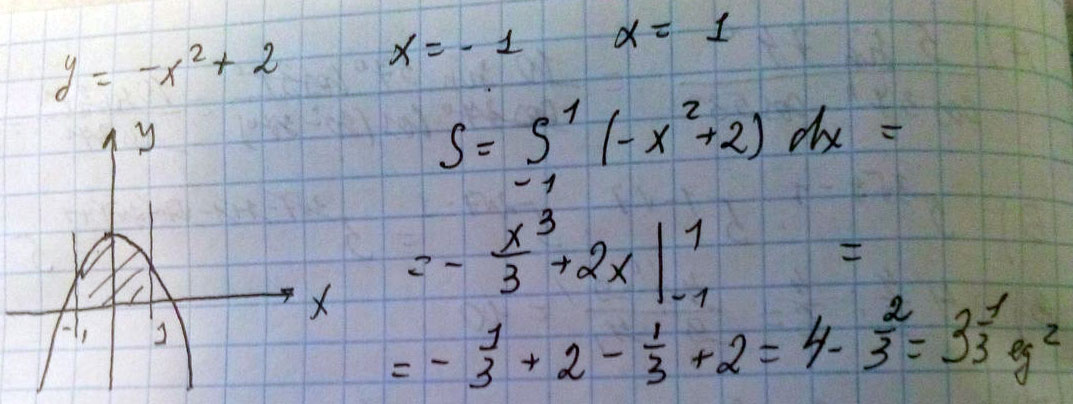интеграл »
найдите площадь фигуры, ограниченной графиком функции - страница 4
1. Вычислите S фигуры, ограниченной линиями: y=x^2; y=0; x=3
2. Вычислите интегралы \(\int\limits^2_{-1} {x^2} \, dx\\ \int\limits^{ \frac{ \pi }{2} }_{0} {-2sinx} \, dx\\ \int\limits^{ \pi /4}_0 { \frac{1}{cos^2x} } \, dx \)
Решение: 1. при у=0 х=0
$$ S= \int\limits^3_0 {x^2} \, dx = \frac{x^3}{3}|^3_0 =\frac{3^3}{3}-\frac{0^3}{3}=\frac{27}{3}=9 $$
2.
$$ \int\limits^2_{-1} {x^2} \, dx = \frac{x^3}{3}|^2_{-1} =\frac{2^3}{3}-\frac{(-1)^3}{3}=\frac{8}{3}+\frac{1}{3}=3 \\ \int\limits^{ \frac{ \pi }{2} }_{0} {-2sinx} \, dx =2cosx|^{\frac{ \pi }{2} }_{0}=2(cos (\pi /2)-cos0)=2(0-1)=-2 \\ \int\limits^{ \pi /4}_0 { \frac{1}{cos^2x} } \, dx =tgx|^{ \pi /4}_0=tg( \pi /4)-tg0= \frac{ \sqrt{2} }{2} $$
Вычислить интеграл \(\int\limits^2_1 {(2x-x^{-2})} \, dx\\ \int\limits^0_{-2} {(0.5x+1)^5} \, dx \)
Найдите площадь фигуры, ограниченной линиями: y=-x^2-4x, y=x+4
y=4x-x^2, y=4-x
Решение: (3)
a)
$$ \int\limits^2_1 {(2x-x^{-2})} \, dx =(2*\frac{x^{1+1}}{1+1}-\frac{x^{-2+1}}{-2+1})|^2_1=(x^2-\frac{1}{x})|^2_1=\\=(2^2-\frac{1}{2})-(1-\frac{1}{1})=3.5 $$
б)
$$ \int\limits^0_{-2} {(0.5x+1)^5} \, dx=(\frac{(0.5x+1)^{5+1}}{0.5(5+1)})|^0_{-2}=(\frac{(0.5x+1)^6}{3})|^0_{-2}=\\=(\frac{(0.5*0+1)^6}{3})-(\frac{(0.5*(-2)+1)^6}{3})=\frac{1}{3} $$
(4)
a)
Найдём точки пересечения графиков:
-x²-4x=x+4
x²+5x+4=0
x1=-4; x2=-1
Далее по формуле: Инт от b до а(f(x)-g(x)dx, где f(x) график расположенный выше графика g(x)
График функции (-x²-4x) расположен выше графика х+4
$$ \int\limits^{-1}_{-4} {((-x^2-4x)-(x+4))} \, dx = \int\limits^{-1}_{-4}(-x^2-5x-4)dx=\\=(-\frac{x^{2+1}}{2+1}-5*\frac{x^{1+1}}{1+1}-4\frac{x^{0+1}}{0+1})|^{-1}_{-4}=(\frac{x^3}{3}-\frac{5x^2}{2}-4x)|^{-1}_{-4}=\\=(\frac{(-1)^3}{3}-\frac{5*(-1)^2}{2}-4*(-1))-(\frac{(-4)^3}{3}-\frac{5*(-4)^2}{2}-4*(-4)=\\=-\frac{1}{3}-\frac{5}{2}+4+\frac{64}{3}+40-16=21-2.5+4+40-60=2.5 $$
б)
Точки пересечения:
4x-x²=4-x
x²-5x+4=0
x1=4; x2=1
График (4x-x²) расположен выше:
$$ \int\limits^4_1((4x-x^2)-(4-x))dx=\int\limits^4_1(-x^2+5x-4)dx=\\=(-\frac{x^{2+1}}{2+1}+5*\frac{x^{1+1}}{1+1}-4*\frac{x^{0+1}}{0+1})|^4_1=(-\frac{x^3}{3}+\frac{5x^2}{2}-4x)|^4_1=\\=(-\frac{4^3}{3}+\frac{5*4^2}{2}-4*4)-(-\frac{1^3}{3}+\frac{4*1^2}{2}-4*1)=\\=-\frac{64}{3}+40-16+\frac{1}{3}-2-4=-21+18=-3 $$
Вычислить площадь фигуры, ограниченной линиями y=3x+18-x^2, y=0
Решение: Пределы фигуры:
Выражение: -x^2+3*x+18=0
Решаем уравнение -x^2+3*x+18=0:
Ищем дискриминант:D=3^2-4*(-1)*18=9-4*(-1)*18=9-(-4)*18=9-(-4*18)=9-(-72)=9+72=81;
Дискриминант больше 0, уравнение имеет 2 корня:
x_1=(2root81-3)/(2*(-1))=(9-3)/(2*(-1))=6/(2*(-1))=6/(-2)=-6/2=-3
;x_2=(-2root81-3)/(2*(-1))=(-9-3)/(2*(-1))=-12/(2*(-1))=-12/(-2)=-(-12/2)=-(-6)=6.
Берем интеграл: -х³/3+3х²/2+18х.
Подставляя пределы, получим:
S = 243/2 = 121.5 кв. ед.Вычислить площадь фигуры ограниченной линиями (через интеграл): x-2y+4=0, x+y-5=0, y=0
Решение: Преобразуем уравнения прямых:
-2у=-х-4 у=0.5х+2
у=-х+5, у=-х+5
Строим их графики: первая прямая проходит через точки (-4;0) и (0;2),
вторая прямая-через точки (5;0) и (0;5).
Находим координату х точки пересечения прямых:0.5х+2=5-х
0.5х+х=5-2,1.5х=3, х=2.
Данная фигура представляет собой два треугольника, которые сверху ограничены: первый от -4 до 2 прямой у=0.5х+2, второй треугольник ограничен прямой у=5-х, точками х=2 и х=5. Следовательно имеем:
2 5 2 5
S=∫(0.5x+2)dx+∫(5-x)dx=(0,25x²+2x)l +(5x-0,5x²)l=0,25·2²-0,25·(-4)²+
-4 2 -4 2
2·2-2·(-4)+5·5-5·2-(0,5·5²-0,5·2²)=1-0,25·16+4+8+25-10-(0,5·25-0,5·4)=
=1-4+4+8+25-10-12,5+2=1+8+25+2-22.5=36-22,5=13,5-ответ.
Проверка: Основание тр-ка:5-(-4)=9, высота у=5-2=3, поэтому S=9·3/2=13.5-ответ совпал
Вычислить площадь фигуры, ограниченной линиями, используя интеграл
y=-x^2+2, y=0, x=-1, x=1
Решение: $$ \int\limits^1_{-1} {(-x^2+2-0)} \, dx = -\int\limits^1_{-1} {x^2} \, dx + \int\limits^1_{-1} {2} \, dx =(-\frac{x^3}{3}+2x)|^1_{-1}=\\ \\ = -\frac{1}{3}+2 - (-\frac{-1}{3}-2)=-\frac{1}{3}+2-\frac{1}{3}+2=4-\frac{2}{3}=\frac{10}{3} $$