найдите площадь фигуры, ограниченной графиком функции - страница 6
Вычислить площадь фигуры ограниченной линиями
у=1/х2
у=1
х=-3
х=-2
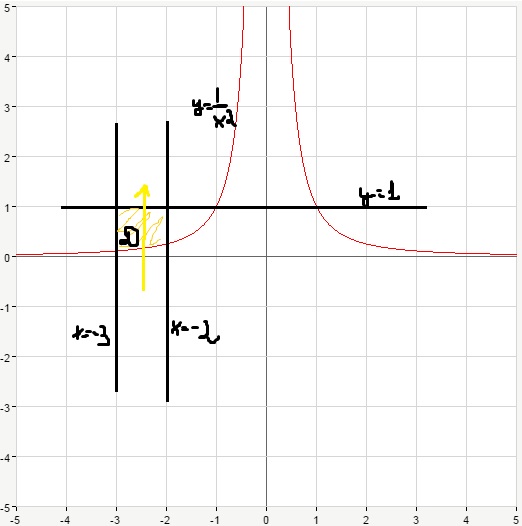
Решение: Делаем рисунок(во вложении).
Находим пределы интегрирования по х и у(для перехода к повторному).
Как видно х изменяется от -3 до -2.
Для у проводим стрелку снизу вверх и смотрим через что она входит в фигуру и выходит. Входит через y=1/x², выходит через y=1.
Нашли пределы, осталось вычислить интеграл:
$$ \iint\limits_{D}dxdy=\int\limits_{-3}^{-2}dx\int\limits_{\frac{1}{x^2}}^{1}dy=\int\limits_{-3}^{-2}(y|^1_{\frac{1}{x^2}})dx=\int\limits_{-3}^{-2}(1-\frac{1}{x^2})dx=\\=(x+\frac{1}{x})|^{-2}_{-3}=(-2-\frac{1}{2})-(-3-\frac{1}{3})=-\frac{5}{2}+\frac{10}{3}=\frac{-15+20}{6}=\frac{5}{6} $$
Не нужно никаких двойных интегралов.$$ S= \int\limits^{-2}_{-3} {(1- \frac{1}{x^2} )} \, dx =(x+ \frac{1}{x} )|^{-2}_{-3}=(-2+ \frac{1}{-2} )-(-3+ \frac{1}{-3} )=1- \frac{1}{6} = \frac{5}{6} $$
1) Найдите общий вид первообразных для функции:
\( f(x)=\frac{1}{3sin^{2}x} +\frac{1}{x^{3}} \)
\( f(x)=1+cos\frac{x}{4} \)
2) Вычислите интегралы
\( \int\limits^1_0 {\frac{dx}{(2x+1)^3}} \, \)
\( \int\limits^\frac{\pi}{8}_0 {(1-2sin^2 2x)} \, dx \)
3) Найдите площадь фигуры ограниченной линиями,
\( y=-x^2-4 \), \( y=x+4 \)
4) Вычислите:
\( \sqrt[3]{-2\sqrt{2}}+ \sqrt[6]{2}*\sqrt[3]{2} \)
\( \sqrt[4]{7+4\sqrt{3}} *\sqrt{2-\sqrt{3}} \)
5) Решите уравнение:
\( \sqrt{x^2+x-3}=\sqrt{1-2x} \)
Решение: 1) $$ f(x)=\frac{1}{3sin^{2}x} +\frac{1}{x^{3}}\\ F(x)=\frac{-ctg x}{3} -\frac{1}{2x^{2}}+c; $$c є R
$$ f(x)=1+cos \frac{x}{4};\\ F(x)=x+4sin \frac{x}{4}+c; $$
2)
$$ \int\limits^\frac{\pi}{8}_0 {(1-2sin^2 2x)} \, dx =\\ \int\limits^\frac{\pi}{8}_0 {cos (4x)} \, dx= \frac{1}{4}sin(4x)| \int\limits^\frac{\pi}{8}_0=\\ \frac{1}{4}(sin (4*\frac{\pi}{8})-sin(4*0))=\\ 0.25*(1-0)=0.25 $$
3) Ищем точки пересечения
$$ -x^2-4=x+4;\\-x^2-4-x-4=0;\\ x^2+x+8=0;\\D=1-4*1*8<0 $$
точек пересечения нет, фигура неограничена, найти площадь не представляется возможным
4) $$ \sqrt[3] {-2\sqrt{2}}+\sqrt[6] {2}\sqrt [3]{2}=\\ \sqrt[3] {(-\sqrt{2})^3}+\sqrt[6] {2}\sqrt [6]{2^2}=\\ -\sqrt{2}+\sqrt[6] {2*2^2}=\\ -\sqrt{2}+\sqrt[6] {2^3}=\\ -\sqrt{2}+\sqrt {2}=0 $$
5) $$ \sqrt{x^2+x-3}=\sqrt{1-2x};\\ x^2+x-3 \geq 0; 1-2x \geq 0;\\ x^2+x-3=1-2x;\\ x^2+3x-4=0;\\ (x+4)(x-1)=0; \\ x_1=-4;\\ x_2=1; $$
1-2*1<0 - корень 1 не подходит
-4 удовлетворяет
ответ: -4
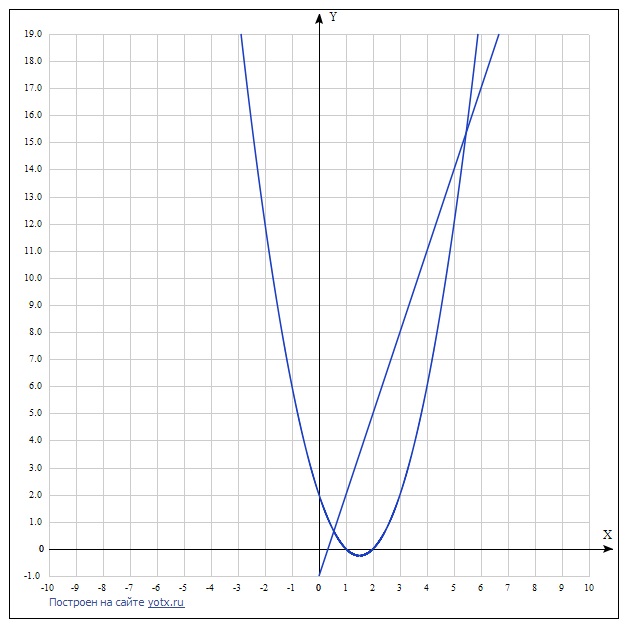
Найдите площадь фигуры, ограниченной линиями y=x^2 -3x+2 и y=3x-1
Решение: $$ x^2-3x+2=3x-1, \\ x^2-6x+3=0, \\ D_1=6, x=3\pm\sqrt{6}, \\ S= \int\limits^{3+\sqrt{6}}_{3-\sqrt{6}} {3x-1-(x^2-3x+2)} \, dx = \int\limits^{3+\sqrt{6}}_{3-\sqrt{6}} {-x^2+6x-3} \, dx = \\ = (-\frac{1}{3}x^3+3x^2-3x)|^{3+\sqrt{6}}_{3-\sqrt{6}} = -\frac{1}{3}(3+\sqrt{6})^3+3(3+\sqrt{6})^2-3(3+\sqrt{6}) + \\ +\frac{1}{3}(3-\sqrt{6})^3-3(3-\sqrt{6})^2+3(3-\sqrt{6}) = \\ \frac{1}{3}(3-\sqrt{6}-(3+\sqrt{6}))((3-\sqrt{6})^2+(3-\sqrt{6})(3+\sqrt{6})+(3+\sqrt{6})^2) + \\ + 3(3+\sqrt{6}-(3-\sqrt{6}))(3+\sqrt{6}+(3-\sqrt{6}))+3(3-\sqrt{6}-(3+\sqrt{6})) = \\ = -\frac{1}{3}\cdot2\sqrt{6}\cdot(9-6\sqrt{6}+6+9-6+9+6\sqrt{6}+6) + \\ + 3\cdot2\sqrt{6}\cdot6-3\cdot2\sqrt{6} = -\frac{2}{3}\sqrt{6}\cdot33 + 36\sqrt{6}-6\sqrt{6} = -22\sqrt{6}+ 30\sqrt{6} = \\ = 8\sqrt{6} $$
Вычислить площадь плоских фигур с помощью интеграла:
f(x)=4-x^2
y=0
y=x+2
Решение: Заданная фигура состоит из двух частей - из треугольника и криволинейной трапеции.
Находим граничные точки.
Крайняя левая точка - пересечение прямой х + 2 с осью ОХ. При этом у = 0, поэтому х + 2 =0 х = -2.
Следующая точка - пресечение прямой х + 2 с параболой 4 - х²:
Приравниваем х + 2 = 4 - х².
х² + х - 2 = 0.
Квадратное уравнение, решаем относительно x:
Ищем дискриминант:D=1^2-4*1*(-2)=1-4*(-2)=1-(-4*2)=1-(-8)=1+8=9;
Дискриминант больше 0, уравнение имеет 2 корня:
x₁=(√9-1)/(2*1)=(3-1)/2=2/2=1;
x₂=(-√9-1)/(2*1)=(-3-1)/2=-4/2=-2.
Теперь находим последнюю точку - пересечение параболы с осью ОХ: 4 - х² = 0 х² = 4 х = +-2. Нужна правая точка х = +2,
Площадь левой части (треугольника) S = (1/2)*3*3 = 4.5.
Правая часть: $$ S= \int\limits^2_1 {(4-x^2)} \, dx =4x- \frac{x^3}{3}| _{1} ^{2} =4*2- \frac{2^3}{3} -4*1+ \frac{1^3}{3} = $$
4 - 7/3 = 1 2/3 = 1.6667.
Общая площадь равна 4,5 + 1,66667 = 6,1667 кв. ед.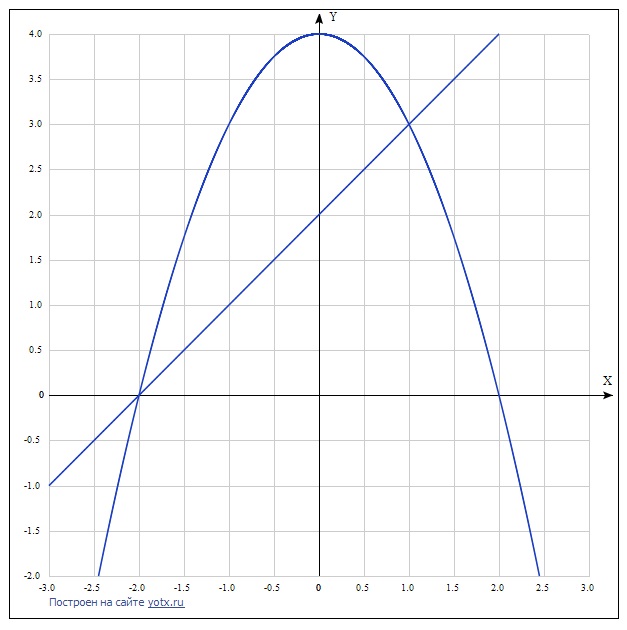
Вычислить площадь плоских фигур с помощью определённого ингеграла.
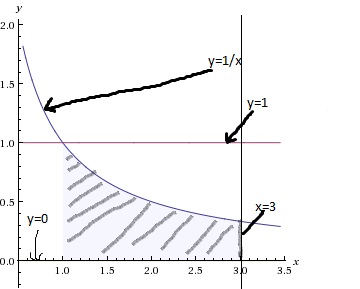
y=1/x; y=1; x=3; y=0
Решение: Дано:
y=1/x
y=1
x=3
y=0.
Найти: Sфиг
Решение
Рисунок смотри в вложении.
$$ \int\limits^3_1 {1- \frac{1}{x} } \, dx = \int\limits^3_1 {x} \, dx - \int\limits^3_1 { \frac{1}{x} } \, dx= $$
| 3
=(x-ln|x|)| =2- ln|3|≈0,9 кв. ед
|1
Ответ: ≈0,9 кв. ед