интеграл »
найдите площадь фигуры, ограниченной графиком функции - страница 7
найдите площадь плоской фигуры, ограниченной линиями у=x^4 и у = 1 с помощью интеграла
Решение: Точки пересечения кривой y = x^4 и прямой y = 1 находим, приравняв уравнения: х1 = 1, х2 = -1. Это пределы интегрирования.
Итак, нам требуется вычислить определенный интеграл от функции y = x^4 по пределам от -1 до 1.
Первообразная равна x^5/5. Подставляем верхний предел, равный 1, получаем 1/5. Подставляем нижний предел, равный -1, получаем - 1/5.
Пользуясь формулой Ньютона-Лейбница, отнимаем от первого значения второе:
1/5 - (- 1/5) = 2/5.
Это и есть искомая площадь.
Ответ: 2/5.Найдем промежутки интегрирования
x^4=1
x^4-1=0
(x²-1)(x²+1)=(x-1)(x+1)(x²+1)=0
x²+1>0при любом х
х-1=0⇒х=1 и х+1=0⇒х=-1
s=S(от -1 до 1)(1-x^4)dx=x-x^5/5(от -1 до 1)=1-1/5+1-1/5=1 3/5кв ед
у=x^4 квадратичная парабола
х -2 -1 0 1 2
у 16 1 0 1 16
у=1-прямая параллельная оси ох
вычислите площадь фигуры, ограниченной линиями y=-x^2+6x-5, y=x-1 (тема: определенный интеграл)
Решение: чертите на координатной прямой два этих графика(будет парабола и прямая)нижний предел интегрирования будет наименьшее значение х удовлетворяющее обоим уравнениям, верхний предел-наибольшее значение
даллее по формуле, интеграл от наим. зн до наиб. зна (-x^2+6x-5-x+1)
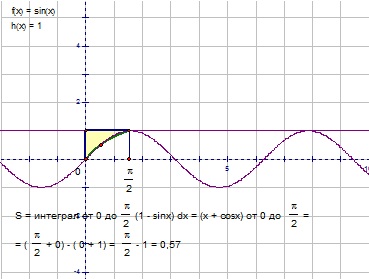
1. Вычислить площадь плоской фигуры, ограниченной линиями: y=sinx, y=l, х=0, х=П/2.(Пи разделить на 2)
2. Боковое ребро наклонной призмы равно 20дм и наклонено к плоскости основания под углом 45 градусов. Найдите высоту призмы.
1. Преобразовать выражение sin2a/sina
2. Высота правильной четырёхугольной пирамиды равна 1см, а сторона основания 4см. Найдите боковое ребро.
1. Найдите боковую поверхность цилиндра с высотой 3 см, если осевое сечение цилиндра плоскостью - квадрат.
2. Исследуйте функцию f(x) = 1/x^6-8x^2 на чётность.
1. Радиус основания конуса 5см, его высота 12см. Найдите площадь осевого сечения, длину образующей.
2. решить уравнение sinx-1/2=0
Решение: В 1) применены формулы интегрирования, формула Ньютона-Лейбница; во 2) теорема Пифагора.1). = (2sina cosa)/sina = 2 cosa
2) y(x) = (1/x^6) - 8x^2; y(-x) = (1/(-x)^6) -8 (-x)^2 = (1/x^6) - 8x^2 = y(x) - функция четная
2) sinx = 1/2, x = (-1)^n * (pi/6) + pi n
Прямая у= -2х+2 пересекает прямую у=х и ось абсцисс в точках АиВ соответственно. Найдите площадь треугольника АОВ, где О-начало координат.
Решение: Находим точку пересечения А прямых у=х и у=-2х+2:
х=-2х+2, 3х=2, х=2/3 и у=2/3(т. к. у=х) А(2/3,2/3)
Точка В - точка пересечения прямой у=-2х+2 и оси ОХ (у=0):
-2х+2=0, 2х=2, х=1, В(1,0)
Основание прямоугольника равно ОВ=1, а высота равна ординате точки А, то
есть 2/3.
S=1/2 * 1*2/3=1/3 (квадратных единиц)
1) Найти площадь фигуры, ограниченной параболами y=x²-1 и y=1-x²
2) Найдите множество значений функции y=-4x², y=tgx-1, y=|x|+4, y=|x-4|
3) Найдите координаты вершины параболы : y=x²+2x
Решение: 1) S =интеграл(1- x² -(x² -1))dx =интеграл 2(1-x²)dx =2(x-x³/3)| a =-1 b=1
=2(1 -1³/3 -(-1 -(-1)³/3 ) =2*2(1-1/3 ) = 8/3.
* * * 1- x² =x² -1⇔2x² =2 ⇔x² =1 ⇒x =± 1 a = -1 ; b=1 * * *
-
2) y = - 4x², E(y) =( -∞ ;0].
y =tqx -1, E(y) =( -∞ ;∞).
y=|x|+4, E(y) =[ 4 ;∞).
y=|x-4|, E(y) =[ 0 ;∞).
-
3) y=x²+2x ;
y=x²+2x= x²+2x +1 -1 =(x+1)² -1. B(-1 ; -1).

