найдите площадь фигуры, ограниченной графиком функции - страница 5
Площадь фигуры ограниченной линиями и интегралы
1) y=x^2, y=0, x=2, x=3
2) y=4-x^2. y=2+x
3) y=4/x. y=5-x
Решение: 1) ∫x²dx = x³/3 | в пределах от 2 до 3 = 3³/3 - 2³/3 =27/3 - 8/3 = 19/3
2) сначала надо найти пределы интегрирования. Для этого решим:
4 - х² = 2 + х
х² + х -2 = 0
По т. Виета х1 = -2 и х2 = 1. На чертеже парабола ветвями вниз и прямая, проходящая через общие с параболой точки (- 2; 0) и (1;3)
Фигура состоит из треугольника, образованного прямой у = 2 +х и криволинейного треугольника Образованного параболой и осью х
S фиг = S Δ + ∫ (4-x²) dx в пределах от 1 до 2 =
= 1/2*3*3 + (4х - х³/3) в пределах от 1 до 2=
= 4,5 + (4*2 -2³/3 - 4*1 + 1/3) = 4,5 +12 - 7/3 = 16,5 -2 1/3= 14 1/6
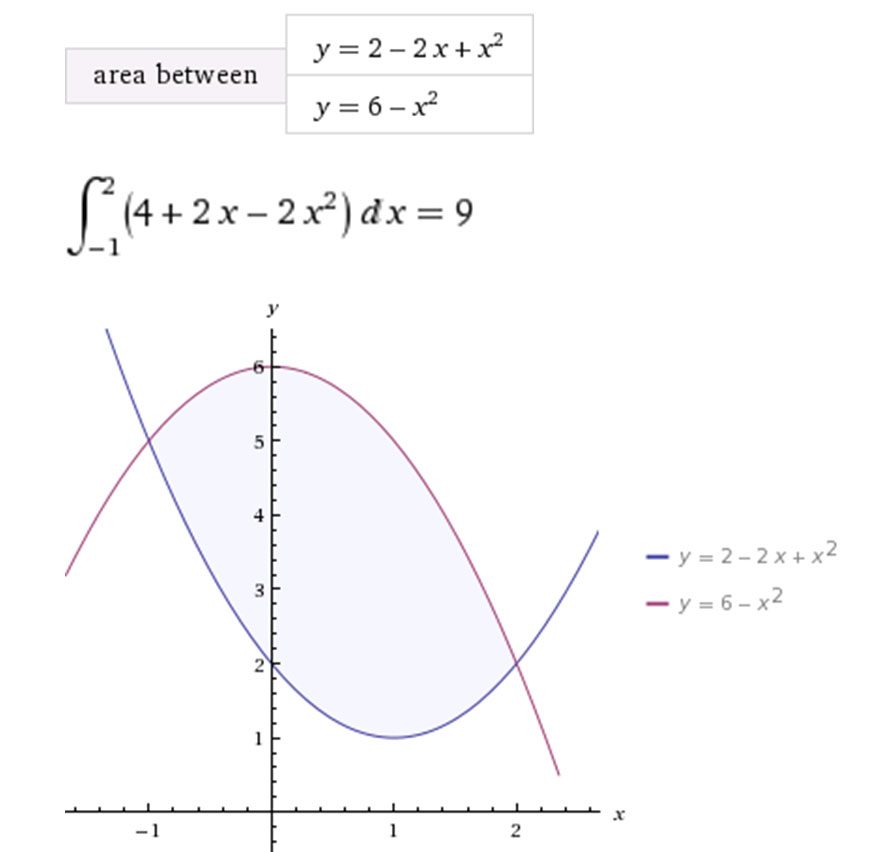
Площадь фигуры D, ограниченной линиями и, определяется интегралом …
Решение: Сначала определяются пределы интегрирования.
Для этого находим точки пересечения графиков заданных функций:
x²-2x+2 = -x² + 6
2x² - 2x -4 = 0 сократим на 2:
х² - х - 2 = 0.
Квадратное уравнение, решаем относительно x:
Ищем дискриминант:D=(-1)^2-4*1*(-2)=1-4*(-2)=1-(-4*2)=1-(-8)=1+8=9;
Дискриминант больше 0, уравнение имеет 2 корня:
x₁=(√9-(-1))/(2*1)=(3-(-1))/2=(3+1)/2=4/2=2;
x₂=(-√9-(-1))/(2*1)=(-3-(-1))/2=(-3+1)/2=-2/2=-1.
Так как графики заданных функций - это параболы, у одной из которых ветви вниз ( это вторая - коэффициент перед х² отрицателен), то заданная площадь определяется вычитанием из верхней нижней:
$$ \int\limits^2_{-1}( {-x^2+6-x^2+2x-2}) \, dx = \int\limits^2_{-1} {(-2x^2+2x+4)} \, dx $$
Найти площадь фигуры ограниченной линиями y=x^2-1, y=3
Решение: Площадь = интеграл от разности "верхней" и "нижней" функции.Верхней здесь является у=3, нижней: y=x^2-1. Пределы интегрирования = точки пересечения графиков (в порядке возрастания расположены), а именно x^2-1=3, x=2 и х=-2. Т. е. пределы интегрирования: от -2 до +2.
интеграл (3 - x^2 + 1) dx = 3x - x^3 /3 + x = 4x - x^3 /3 = x*(4 - x^2 /3)
Подставляем вначале верхнее значение (+2), затем отнимаем значение при нижнем (-2):
2*(4-4/3)=2*(8/3) = 16/3
-2*(4-4/3) = -16/3
16/3 + 16/3 = 32/3 - это и есть площадь фигуры.
Вычислить площадь фигуры, ограниченной линиями(при помощи определённого интеграла)
y=x^2-6, y=-x^2+5*x-6
Решение: Вычислить площадь фигуры, ограниченной линиями: y₁=x+2, y₂=2x - (x^2/2) + 6или y = -0,5х² + 2x + 6 и y=x+2
для выявления пределов интегрирования найдём точки пересечения графиков этих двух функций, приравняв их правые части
-0,5х² + 2x + 6 = x + 2
-0,5х² + x + 4 = 0
или
-х² + 2х + 8 = 0
D = 4 + 32 = 36
√D = 6
x₁ = (-2 + 6):(-2) = -2
x₂ = (-2 - 6):(-2) = 4
Итак, интегрируем в пределах: -2 и 4.
Теперь надо решить, какая из функций проходит выше другой
найдём вершину параболы f(x) = -0.5х² + 2х + 6
m = -2:(-1) = 2; n = -2+ 4 + 6 = 8
в точке х = 2 прямая y=x+2 имеет у =4, а кривая y = -0.5х² + 2х + 6 имеет у = 8
в точке x₁ = -2 и в точке x₂ = 4 значения обеих функций совпадают.
Очевидно, что парабола в интервале от -2 до 4 проходит выше.
Находим интеграл
∫(у₂ - у₁)dx = ∫(-0.5х² + 2х + 6 - (x+2))dx =
= ∫(-0.5х² + х + 4)dx =
= -х³/6 + х²/2 + 4x
Подставим пределы и вычислим площадь
S = 8/6 + 4/2 - 4·2 - (-64/6 + 16/2 + 4·4) =
= 4/3 + 2 - 8 + 32/3 - 8 + 16 = 14
Ответ: S = 14
Найдите площади фигур, ограниченных линиями. y= -x^2 +2x+3, y=0
Решение: Y = - x² +2x +3 ; y = 0.
y = 4 - (x - 1)² *** = (2 - x +1 )(2+x -1) = -(x+1)(x-3) ***
y =4 при x=1
График этой функции парабола вершина которой в точке x = 1 ; y = 4 : G(1 ;4).
Ветви направлены вниз. Определим точки пересечения с осью y и x
с осью y : x = 0 ⇒y = - 0² +2*0 +3 =3 =3 т. е. точка A(0 ;3)
с осью x : y = 0 ⇒ 0 = - x² +2x +3
x² -2x -3 = 0 ;
x₁= -1;
x₂ = 3.
S = интеграл ((a) => (b)) (ydx) = интеграл ((a) => (b)) ( - x² +2x +3 )dx) ;
границы интегрирования a = x₁= -1 ; b=x₂ = 3.
S = интеграл ((-1) => (3)) ( - x² +2x +3 )dx) =( -x³/3 +x² +3x) | (-1) =>(3) =
=( -3³/3 +3² +3*3 ) - ( - ( -1)³/3 +( -1)² +3 (-1)) = 9 -(-5/3) =32/3.
-
* * * * *F(b) -F(a) формула Ньютон - Лейбница * * * * *
ответ : 32 / 3.

