модуль »

график функции модуль х

  • По стройте график функции и определите, при каких значениях прямая y=x^2-6|x|+2x имеет с графиком ровно три общие точки.


    Решение: Нули подмодульного выражения разбивают исходную функцию на две со строгими областями определения.
    Т. е. всё что правее нуля(включая его) и левее нуля(не включая нуля) делает модуль со строго фиксированным знаком.
    Возьмём -3 - из модуля 3,3 - отрицательно, при раскрытии выставим знак - как множитель -1.
    Возьмём 2 - из модуля 2. Просто снимаем скобку.
    Возьмём 0 - из модуля 0. Также модуль "просто снимается" и с положительными числами, поэтому придумали просто снимать знак модуля, если выражение неотрицательно (больше либо равно нуля)
    Это примеры.
    Дальше.
    Нуль вашего подмодульного выражения есть нуль, поэтому если х<0, то при раскрытии функции вы выставите знак -(модуль отрицат. быть не может);
    если х>=0, знак при раскрытии снимите. Это вся суть.
    y=x^2-6|x|+2x.⇔y=(фигурн. скобка)
    х^2-6*(-1)*х+2х, если x<0
    x^2-6х+2х, если x>= 0.

  • Построить график функции у=|х^2 + х - 1|
    Найти точки пересечения с осями


    Решение: строим график функции: y=x^2+x-1; x=0; y=-1; y=0; x верш=-1/2=-0,5; ув=-1,25; x=1; y=1 и все что находится по оу меньше 0, симметрично отражаем; Вот график: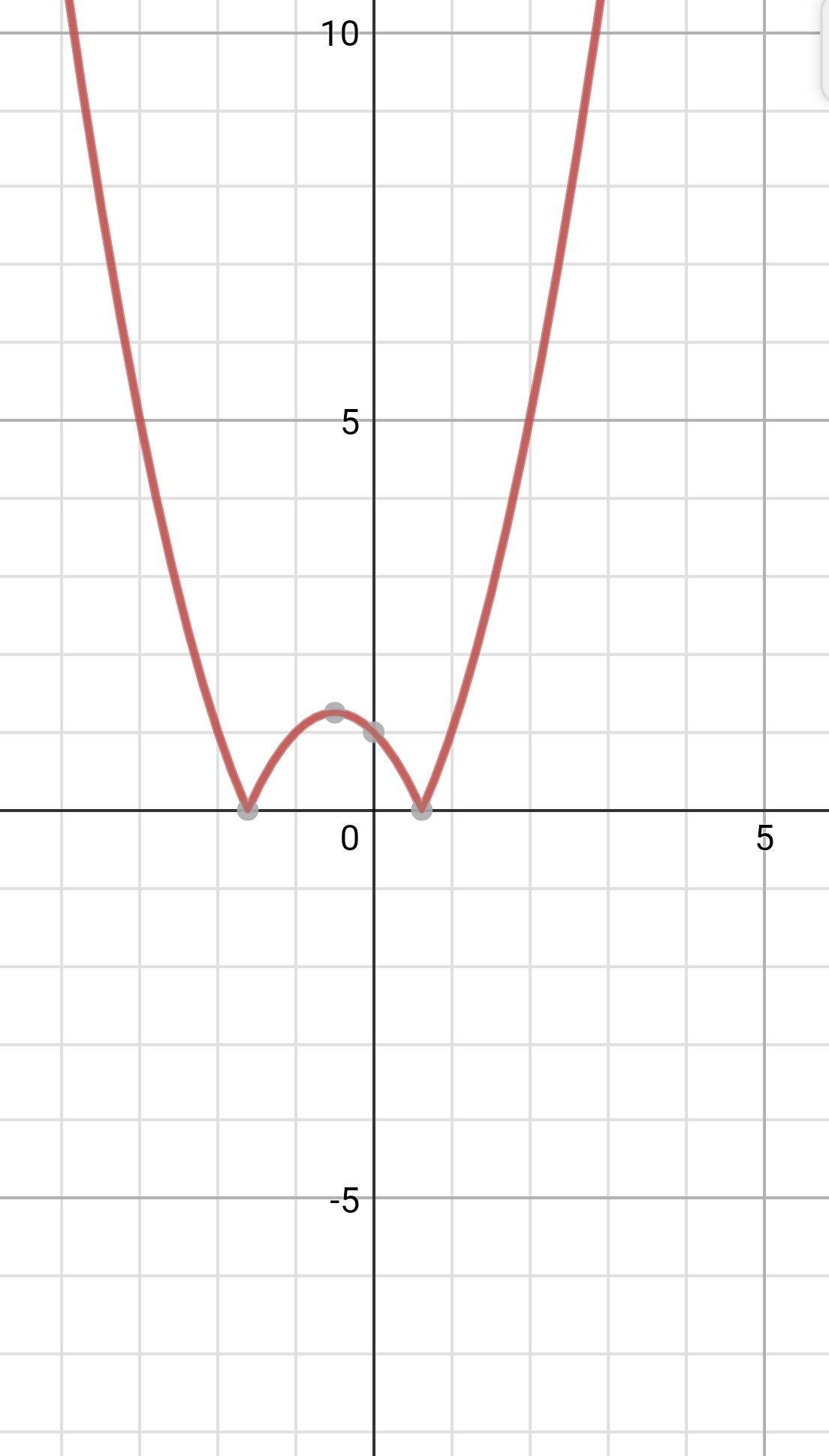

    строим график функции y x x- x y - y x верш - - ув - x y и все что находится по оу меньше симметрично отражаем Вот график...

  • Постройте график функции у= I х^2-4х+3 I и напишите свойства функции.
    Если что, I I-это функция у= IхI, модуль.
    x^2- х в квадрате.


    Решение: У=|x²-4x+3|
    . Строим у=х²-4х+3. Оставляем все что выше оси ох, а то что ниже  отображаем наверх
    y=(x-2)²-1
    Парабола у=х², ветви вверх, вершина (2;-1), х=2-ось симметрии. Точки пересечения с осями ((1;0);(3;0);(0;3)
    D(x)∈(-∞;∞)
    E(y)∈[0;∞)
    Убывает при x∈(-∞;1] U [2;3]
    Возрастает при  х∈[1;2] U [3;∞)
    y>0 x∈(-∞;∞)
    y<0  нет
    ymin=0,ymax-нет

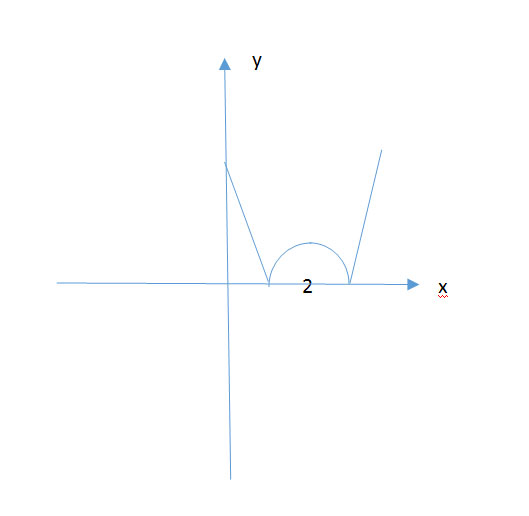
    У x - x . Строим у х - х . Оставляем все что выше оси ох а то что ниже  отображаем наверхy x- - Парабола у х ветви вверх вершина - х -ось симметрии. Точки пересечения с осями...

  • Постройте график функции игрек равно 3,5 модуль из икс минус 1 деленное на модуль из икс минус 3,5 икс в квадрате и определите При каких значениях K прямая Y равно KX имеет с графиком общих точек


    Решение: Y=(3,5|x|-1)/(|x|-3,5x²)
    1)x<0
    y=(-3,5x-1)/(-x-3,5x²)=-(3,5x+1)/[-x(1+3,5x)]=1/x, x≠-2/7 y≠-3,5
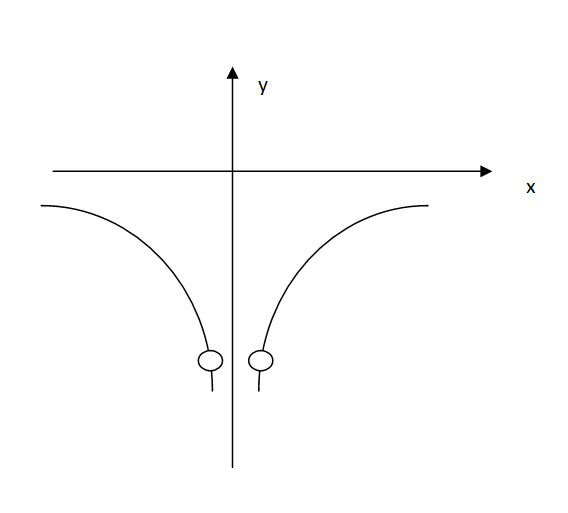
    гипербола у=1/х в 3 ч, точка(-2/7;-3,5) выколота
    2)x>0
    y2=(3,5x-1)/[x(1-3,5x)]=-1/x,x≠2/7 y≠-3,5
    гипербола у=-1/х в 4 ч, точка(2/7;-3,5) выколота
    при к=0, к=49/4 и к=-49/4 прямая у=кх не имеет общих точек с графиком

    Y x - x - x x lt y - x- -x- x - x -x x x x - y - гипербола у х в ч точка - - выколота x gt y x- x - x - x x y - гипербола у - х в ч точка - выколотапри к к и к - прямая у кх...

  • Построить график функций и написать свойства
    1. у=1/2(одна вторая) х2(х в квадрате)
    2. у=корень из х
    3. у=[х] (модуль)


    Решение: 1. у=1/2 х2
       Это парабола, направленная веточками вверх и вытянута в 2 раза относительно оси ординат. (синим - стандартная парабола у=х2)
    2. у= корень из х
       Это веточка параболы, направленная вправо.
    3. у= |x|
       Это так называемая "галочка" - биссектриса первого и второго квадрата.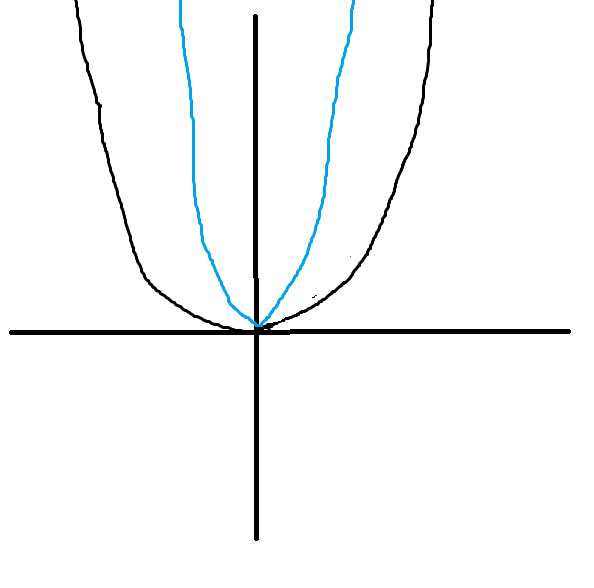

    . у х    Это парабола направленная веточками вверх и вытянута в раза относительно оси ординат. синим - стандартная парабола у х . у корень из х   Это веточка параболы направл...
1 2 3 > >>