модуль »

график функции модуль х - страница 2

  • Постройте график функции у=модуль х(х-2)+2 и определите, при каких значениях прямая у=m имеет с графиком ровно две общие точки.


    Решение: ...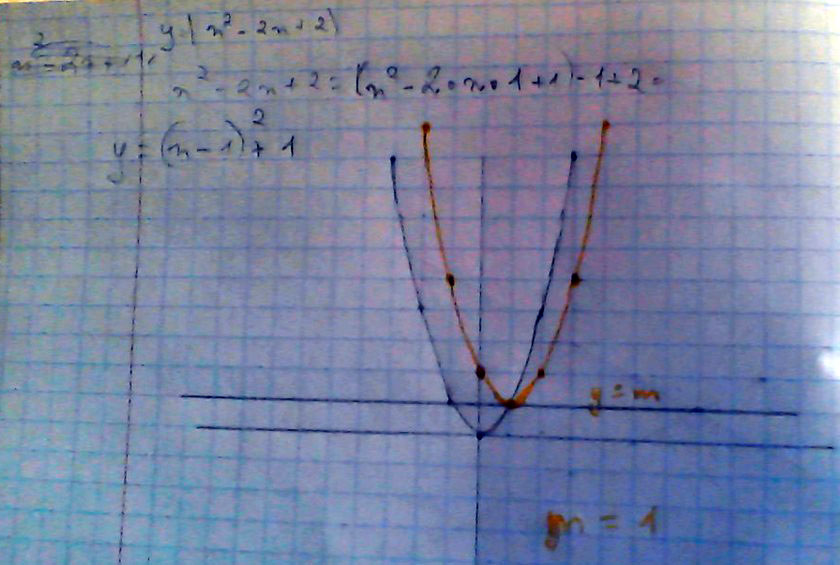

  • Постройте график функции
    у=-х²+3*модуль х
    и определите при каких значениях параметра а прямая у=а имеет с графиком данной функции две общие точки.
    В ответе должно получиться (-бесконечности;0) ; 2,25.


    Решение: Так как |x|=x при х>=0, а |x|=-x при х<0, то надо  рассмотреть два случая. чтобы построить график. Смотри во вложении рисунок.  На нём видно, что прямая у=m (прямая,  параллельная оси ОХ, проходящая через точку (0,m))  пересекает график заданной функции один раз только тогда, когда m>0.
    Вложение не добавляется, поэтому график опишу словами. Правее оси ОУ рисуем часть параболы у=x^2-3x. Она пересекает эту ось  в точках х=0 и х=3, ветви вверх, вершина в  точке (1,5 ; -2,25). Левее оси ОУ рисуем часть параболы у=-x^2+3x. Она пересекает ось ОХ  при тех же значениях переменной, то есть х=0 и х=3,  но ветви у неё вниз и вершина в точке (1,5 ; +2,25).  Главное для графика - это то, что параболы (а вернее их части) должны  быть нарисованы одна в правой полуплоскости (правее оси ОУ),  а другая в левой полуплоскости (левее оси ОУ)

  • Выполнить график функции: y=x(|x|- 4)


    Решение: Нужно рассмотреть два случая когда x<0 и раскрыть знак модуля поставив перед ним знак - И когда x> либо равно 0. И просто раскрыть знак модуля как простые скобки.

    Нужно рассмотреть два случая когда x либо равно . И просто раскрыть знак модуля как простые скобки....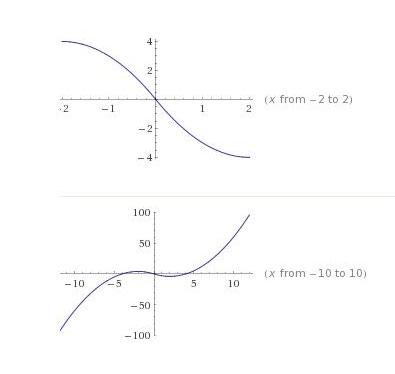

  • Как начертить график функций
    у=х^2-2, если модуль х больше либо равно 2


    Решение: у=х²-2 парабола, вершина в точке (0 -2)

    находим ещё несколько точек

    х   1    -1  2  -2    3 -3  

    у   -1   -1     2   2     7   7

    строим параболу и оставляем у часть где х>2  x<-2

    1) график функции y=x² сместить вниз по осиОy на 2;
    2) из точек x=2;x=-2 провести линии параллельно Оy до пересечения с графиком y=x²-2;
    3) графиком функции y=x²-2; при |x|≥2 является :
    ветвь x(-∞;-2) и ветвьx(+2;+∞)

  • 1. Чему равно отношение ординат двух точек графика функции у = х^3 если отношение их абсцис равно 3?

    2. Какие значения может принимать функция у = f(х + 1) - f(х) на множестве действительных чисел, если функция f(х) возрастает на этом множестве?

    3. Какие координаты имеет центр симметрии графика функции у = (х + 1)^3?

    4. Какое геометрическое место точек является графиком уравнения 4х^2 + у^2 - 4ху -4х + 2у = 0?

    5. Чему равна площадь, заданной системой неравенства? модуль х < или = 2 модуль у < или = х


    Решение: 1. $$ \frac{y_2}{y_1}=\frac{x^3_2}{x^3_1}=(\frac{x_2}{x_1})^3=3^3=27 $$

    2.$$ y=f(x+1)-f(x)>0; $$ так как для возрастающей функции $$ f(x+1)>f(x) $$ по определению

    ПОЛОЖИТЕЛЬНЫЕ ЗНАЧЕНИЯ

    3. Вершина кубической параболы (-1;0)

    4. $$ 4x^2+y^2-4xy-4x+2y=0;\\\\(4x^2-4xy+y^2)-(4x-2y)=0;\\\\(2x-y)^2-2(2x-y)=0;\\\\(2x-y)(2x-y-2)=0; $$

    пара паралельных пряммых 2x-y=0 и 2x-y-2=0

    5. $$ |x| \leq 2; |y| \leq x; $$ - єто квадрат со стороной 4, его площадь 4*4=16 единиц

<< < 12 3 4 > >>