модуль »

график функции модуль х - страница 4

  • Постройте график функции y = -|x^2+9x|.
    Он с модулем.


    Решение: Таблица и график во вложении

    Y=-x²+9x.
    Решим уравнение -x²+9x+0:
    a=-1. b=9. c=0
    D=b²-4ac=9²-4·1·0=81-0=81;
    X₁,₂= -b+-√D=-9+-√81=-9+-9=X₁=-9+9=0; X₂=-9-9=-18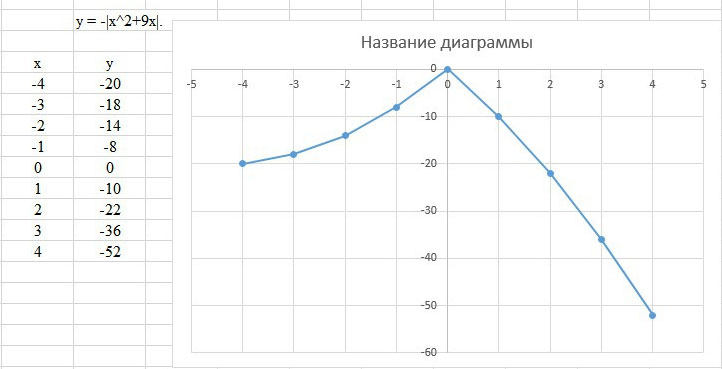Таблица и график во вложении Y -x x.Решим уравнение -x x a - . b . c D b - ac - - X  -b - D - - - - X - X - - -...

  • 1. решить уравнение 3(x-2)-9x=1
    2. построить график функции y=2x-2
    3. решить систему уравнений |y-2x=2
    |2x-4y=8
    4. решить задачу: первая сторона треугольника в 2 раза больше второй стороны и на 3 см меньше третьей. Найдите каждую сторону, если периметр треугольника равен 46см.
    5. решить уравнение с модулем |x+3|-4=0


    Решение: 1. 3(х-2)-9х=1
     3х-6-9х=1
    -6х=7
    х=-7\=-1 1\6
    проверка:3*(-7\6)-6-9(-7\6)=1
      -7\2-6+21\2=1
      1=1
    2. y=2x-2
    x= -1 0 1
    y= -4 -2 0
    строй график по координатам (-1;-4), (0;-2), (1;0)-будет прямая
    4.2х см-первая сторона
      х см -вторая сторона
      2х+3 см -третья сторона
    Р=46 см
    2х+х+2х+3=46
    5х=43
    х=43:5
    х=8.6 см - вторая сторона
    2*8.6=17.2 см - первая сторона
    17.2+3=20.2 см - третья сторона
    3. у-2х=2
      2х-4у=8
    у=2+2х
    2х-4(2+2х)=8
    2х-8-8х=8
    -6х=16
    х=-2 2\3
    у=2+2*(-8\3)=2-5 1\3=-3 1\3
    проверка:-3 1\3-2*(-2 2\3)=-10\3+16\3=6\3=2
    2(-2 2\3)-4(-3 1\3)=-16\3+40\3=24\3=8
    5.
    х=4-3
    х=1

  • Построить графики функций с модулями y=|sinx|, y=|cosx|, y=|tgx|


    Решение: Сначала строим данные функции без модуля, а потом отрицательную часть отображаем на верхнюю положительную полуплоскость. Понятно, что эти функции периодические

    Сначала строим данные функции без модуля а потом отрицательную часть отображаем на верхнюю положительную полуплоскость. Понятно что эти функции периодические...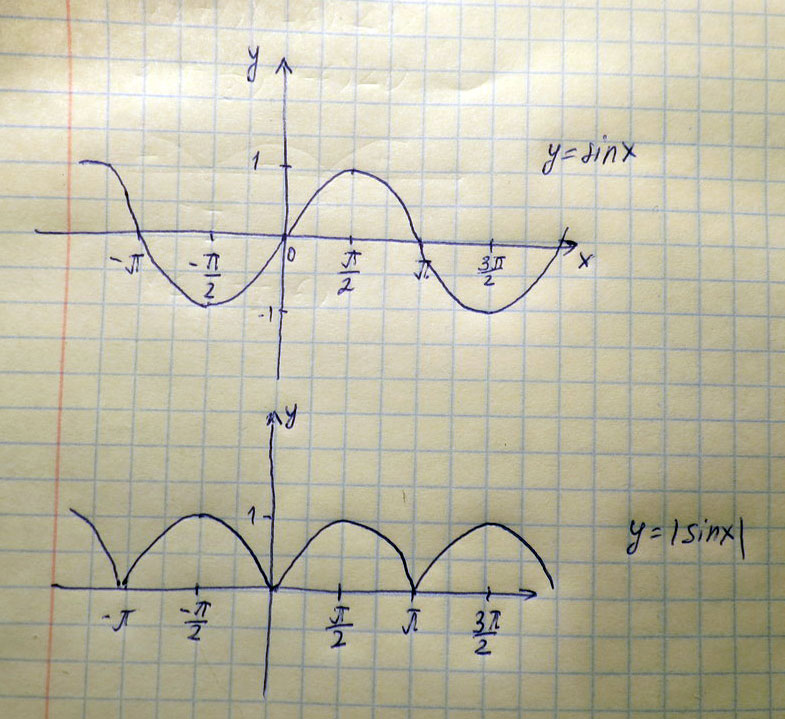

  • Преобразовать и написать график функции y= | x^2 + x - 2 | в модуле.


    Решение: Y=|x²+x-2| график такого типа строим в 2 действия.
    1. строим y=x²+x-2 пунктиром
    корни -2 и +1, при х=0 у=-2 вершина х0=-b/2a=-1/2
    y0=1/4-1/2-2=-2.25
    2. всю часть пунктирного графика, которая лежит ниже оси Х,
    отражаем зеркально относительно  нее вверх и получившийся график обводим жирно.

  • Постройте график функции у= |х в квадрате +6х +5| и найти значения в которых график пересечет прямая м=у ровно в трех точках.


    Решение: Чтобы построить этот график необходимо построить график квадратичной функции без модуля и часть графика, которая ниже оси х зеркально отразить относительно оси х.
    Для того чтобы построить график квадратичной функции (парабола) найдем вершину и точки пересечения с Ох.
    Хвершины=-b/2a=-3
    Yвершины=(-3)²+6*(-3)+5=-4
    Итак, наша вершина (-3;-4) и она зеркально отразится в точку (-3;4)
    Парабола пересекает Ох в точках х²+6х+5=0, х=-1 и х=-5
    прямая у=м параллельна оси х и будет пересекать график в 3 точках когда будет проходить через обе ветви параболы и ее отраженную вершину, а это будет когда м=4

    .
    Прямая у=4 пересекает график в 3 точках (-3;4),(-3-2√2;4) и (-3+2√2;4)

    Чтобы построить этот график необходимо построить график квадратичной функции без модуля и часть графика которая ниже оси х зеркально отразить относительно оси х.Для того чтоб...
<< < 234 5 > >>