модуль »
график функции модуль х - страница 3
Постройте график функции
у=х^2/{х}
где { } модуль
с рисунком
Решение: Так как и \(x^{2}\) и модуль х - числа неотрицательные, то модуль можно убрать и останется у=х
PS главное при чертеже стереть все что слева от оси Y и начертить рисунок
зеркальныйОДЗ
x≠0
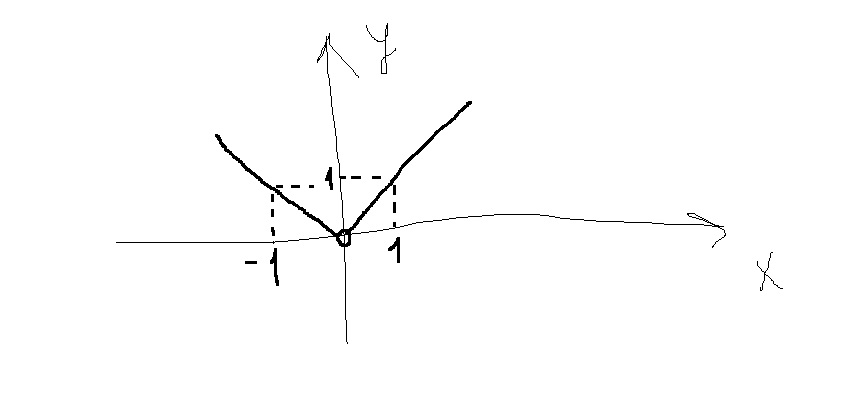
$$ y= \dfrac{x^2}{|x|} \\\\\\1) \, x>0\\\\y= \dfrac{x^2}{x} =x\\\\2)x<0\\\\y= \dfrac{x^2}{-x}=-x \\ y= \left \{ {{x,\quad x>0} \atop {-x,\quad x<0}} \right. $$
(график как у функции модуля, но точка(0,0) -выколотая)
Построить график функции у= sin модуль х
Решение: Строим график на положительных x, а затем симметричный относительно оси ординат для отрицательных x. Получаем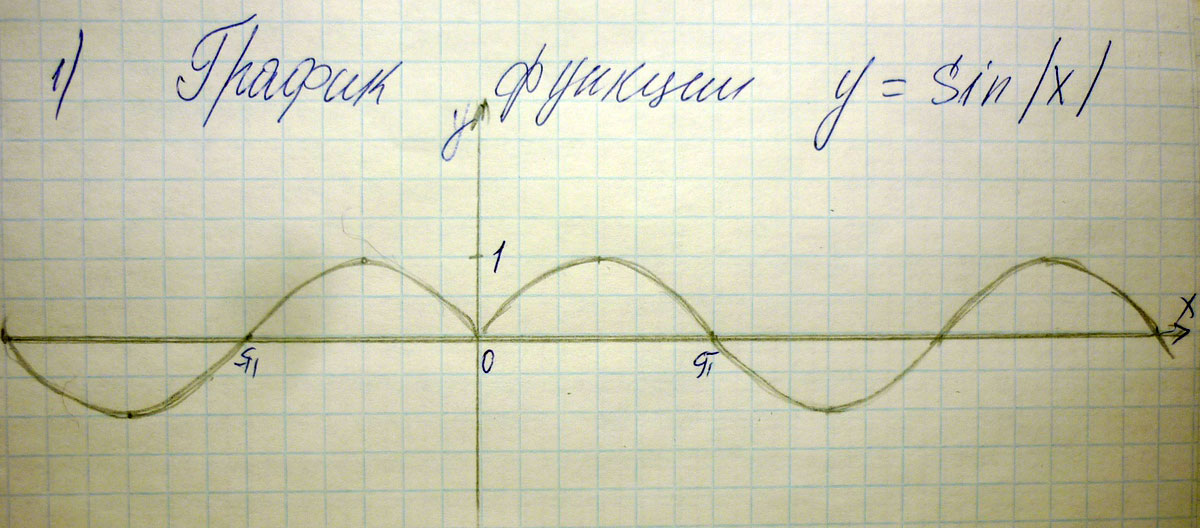
3. Найдите в таблице 3 графики линейных функций, у которых угловые коэффициенты:
а) равны;
б) равны по модулю и противоположны по знаку.
Решение: Линейные функции - это прямые, они изображены на рисунках 1-7, 9
а) если угловые коэффициенты равны, то прямые либо совпадают, либо параллельны друг другу: 6, 1-3 (на рис. 3 есть прямая, совпадающая с прямой на рис. 1), 3-7 (по одной прямой с каждого рис. они параллельны), 5-7 (параллельны), 5-6
б) угловые коэффициенты равны по модулю - прямые будут симметричны:
1-2, 4-5, 7, 1-3Как построить график функции с модулем? Объясните, на примере у=|х+2|+|х-2|
Решение: Модуль говорит о перемене знака например |5x-10|
Открываете модуль и получите сначала просто 5х-10, а потом тоже самое, только с "-" перед Х(т. е х становится отрицательным) 5*(-х)-10
у=|х+2|+|х-2|
Так как у тебя два модуля, то раскрывая, у тебя получится 4 функции
1) у=х+2+х-2 (положительная)
2) у=-х-2-х+2 (отрицательная)
3) у=х+2-х+2 (первая часть положительная, вторая-отрицательная)
4) у=-х-2+х-2 (первая часть отрицательная, вторая-положительная)
Отсюда приводим подобные:
1) у=х+2+х-2 =2x (прямая)
2) у=-х-2-х+2 =-2x (прямая)
3) у=х+2-х+2 =4 (это просто прямая по y, которая равна 4)
4) у=-х-2+х-2 =-4 (это просто прямая по y, которая равна -4)
После построения находятся пересечения (они должны быть указаны).
)Построить график функции y=log2(x). Задание с модулем
Решение: Строим график y=log2(x), по свойству 2>1 - функция возрастающая, график y=log2(x+2) - перенести на 2 еденицы влево, потом отображаем относительно оси Оу.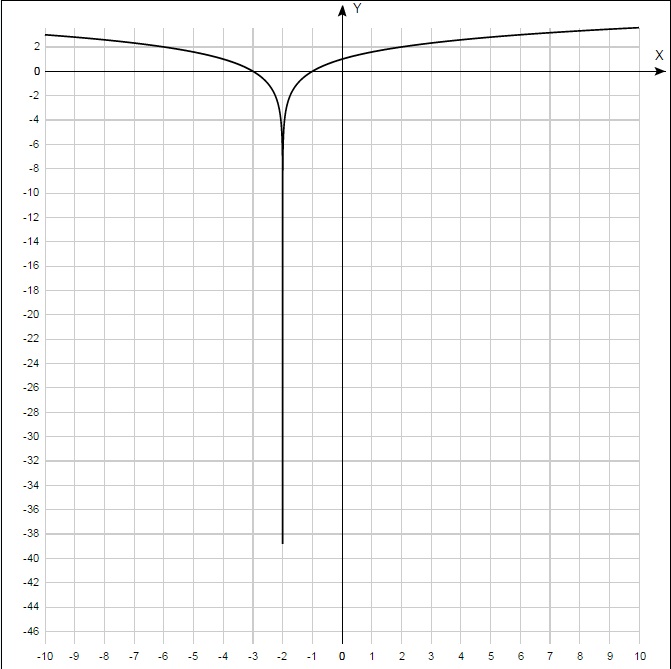


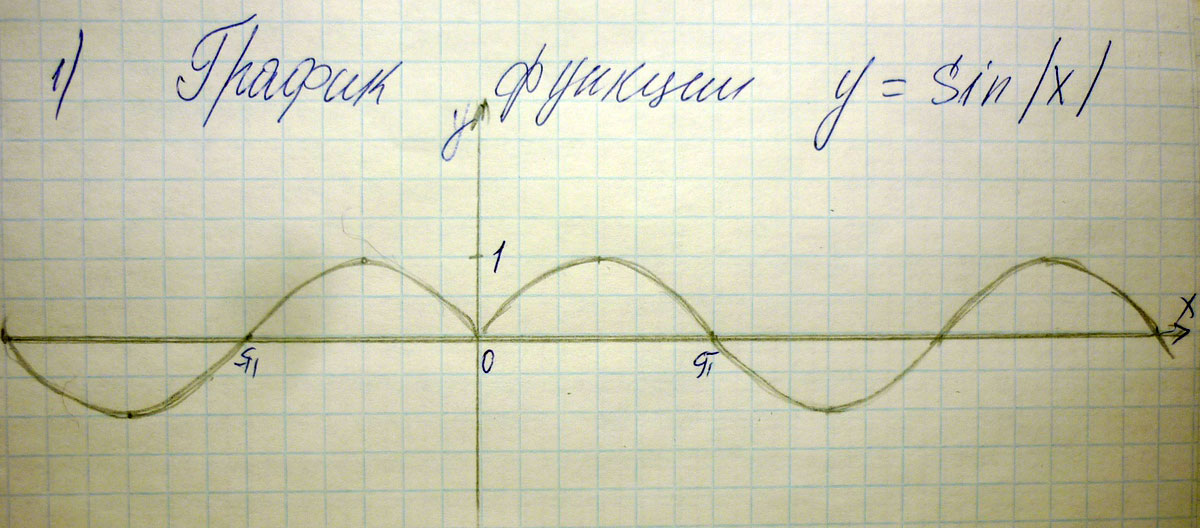

 Два противоположных числа, например +6 и -6, отличаются знаками, но записываются одинаковыми цифрами. Говорят, что они имеют одинаковые абсолютные величины. Абсолютная величина каждого из них равна 6.
Модулем (абсолютной величиной) положительного числа является само это число, модулем отрицательного числа - противоположное ему число, модулем числа 0 - само число 0. То есть под модулем числа понимается абсолютная величина, абсолютное значение этого...
Два противоположных числа, например +6 и -6, отличаются знаками, но записываются одинаковыми цифрами. Говорят, что они имеют одинаковые абсолютные величины. Абсолютная величина каждого из них равна 6.
Модулем (абсолютной величиной) положительного числа является само это число, модулем отрицательного числа - противоположное ему число, модулем числа 0 - само число 0. То есть под модулем числа понимается абсолютная величина, абсолютное значение этого... Уравнения с модулем
Пример 1. Решить уравнение |10х – 5| = 15.
В соответствии с правилом, уравнение равносильно совокупности двух уравнений:
│10х – 5 = 15 │10х – 5 = –15
Решаем:
│10х = 15 + 5 = 20 │10х = –15 + 5 = –10
↕
│х = 20 : 10 │х = –10 : 10
↕
│х = 2 │х =...
Уравнения с модулем
Пример 1. Решить уравнение |10х – 5| = 15.
В соответствии с правилом, уравнение равносильно совокупности двух уравнений:
│10х – 5 = 15 │10х – 5 = –15
Решаем:
│10х = 15 + 5 = 20 │10х = –15 + 5 = –10
↕
│х = 20 : 10 │х = –10 : 10
↕
│х = 2 │х =...