уравнение модуль х

Найти мах целое значение параметра а при котором уравнение имеет 2 корня [x+3](x-3) разделить на а-3 =1
х+3 под знаком модуль

Запишем уравнение в виде
|x+3|(x-3)=a-3
а≠3
Строим график функции
у=|x+3|(x-3)
 
На (-∞;-3)
|x+3|=-x-3
cтроим график у=-х²+9
на [-3;+∞)
|x+3|=x+3
строим график у=х²-9

График функции  у=a-3   при разных значения а - прямые, параллельные оси ох.
Графики такого вида пересекаются с графиком у=|x+3|(x-3) в двух точка только в двух случаях
a-3=0, но по условию а≠3
или
a-3=-9  ⇒  а=-6

О т в е т. при а = - 6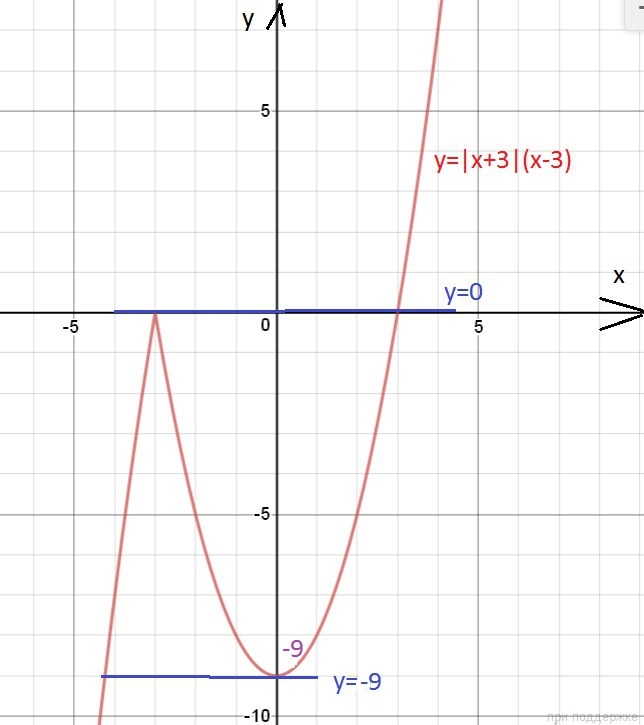

решить уравнения
1.5*(-1+9x)-5=-1
*- это умножить
2. x/6+x/12+x= -34/4
/- это дробь
Минус относится к полной дроби
3. (2x+5)*(8-x)=0
*- это умножить
4. x/-5= -7/9
Минус относится к 7
5. |x-3|=8
|- это модуль

1)5-45х-5=-1 -45х=-1 Х=1/45 2) х/6 + х/12+х=-34/4 (2Х+х+12х)/12= -34/4 15х/12=-34/4 15х=-102 Х=6,8 3)(2х+5)(8-х)=0 16х-2х^2+40-5х=0 2х^2-11х-40=0 Д=21 Х1=-2,5 х2= 8 4) х/-5=-7/9 9х=35 Х=35/9 Х=3 8/9 5){х-3}=8 Х-3=8 Х=11 Или -х+3=8 -х=5 Х=-5

Помогите решиь тест
1) Мастер, делая по 18 деталей в час, изготовил все детали за 5 часов. Если он будет делать по 20 деталей в час, то за часов изготовит все детали
2) Сравните числа: -2/5и-3/4
3) Выполните действие:(-9,2:4 целых3/5+3целых1/4)*(-0,8)-Просто ответ
4) Тоже самое:-8*(-7+23):64-3
5) Решите уравнение 5х+2=1/2
/////-палочка
9
6) Решите уравнение (2х+3)-1,5=-0,5
7) Решите уравнение /2х+3/=19 //-Это модуль
8) Решите уравнение (3х-1)(х+4)=0
9) Представьте в виде десятичной периодической дроби число:2целых3/22

1)18*5=90 деталей за 5 часов
90:20=4,5 часов
2)-2/5<-3/4,0,4<-0,75
3)(-9,2:4 3/5+3 1/4)*(-0,8)=-1
4)-8*(-7+23):64-3=-5
5)5х+2=1/2
5х=-1,5
х=-1,5:5
х=-0,3
6)(2х+3)-1,5=-0,5
2х=-0,5+1,5-3
2х=-2
х=-1
7)|2х+3|=19
2х=19-3
2х=16
х=16:2
х=±8
8)(3х-1)(х+4)=0
3х-1=0
3х=1
х1=1/3
х+4=0
х2=-4
Ответ: х1=1/3
9)2 3/22=47/22=2,136(36)

х - 4 = модуль х-2 дробь х -2

Решите уравнение

Первый случай:

x-4=(x-2)/(x-2)

x-4=1

x=5

Второй случай:

x-4=-(x-2)/(x-2)

x-4=-1

x=3

Ответ: x=3; x=5

$$ x-4=\frac {|x-2|}{x-2}; $$

если х-2>0 т. е. x>2, то |x-2|=x-2 и уравнение принимает вид

x-4=1

x=4+1

x=5 - удовлетворяет

если х-2<0 т. е. x<2, то |x-2|=-(x-2) и уравнение принимает вид

x-4=-1

x=4-1

x=3 - не удовлетворяет

ответ: 5

( - 2 дробь 3 + 5 дробь 12) + (- 0,45)=

I I- это модуль числа

Ix - 3I=-6-сколько решений имеет это уравнение

Ix - 3I=-6

имеет 2 решения

1) когда $$ Ix - 3I\geq0 $$ 2)Ix - 3I<0

тогда x-3=-6 тогда -x+3=-6

  x=-6+3 -x=-6-3

  x=-3 -x=-9

  x=9

Сума модулей корней квадратного уравнения 4x²+kx-3=0 равно 2,
при этом модуль отрицательного корня больше от положительного. Найти k

Как мне кажется решение будет такое

Решить уравнение
l l - модуль
X - переменная
> - знак "больше"
< - знак "меньше"
УР-Е: lxl + l2x-1l - x > 1

Уравнения с модулем.
|1-2x| = 3x-2;
|6x²-1|=5;
x²-7|x|+6=0

1) |1-2x|=3x-2 В модуле рассматриваются 2 случая, 
Если 1-2x>0, то 
1-2x=3x-2
5x=3
x=3/5
Если 1-2x<0, то
2x-1=3x-2
x=1
Ответ: $$ x_1= \frac{3}{5}; x_2=1 $$
2)|6x²-1|=5
$$ 6x^2-1=б5 $$
a) 6x²-1=5
6x²=6
$$ x=б1 $$
b) 6x²-1=-5
6x²=-4
x²≠-4/6 - ответ не удовлетворяет условии. ⇒
Ответ:$$ x=б1 $$
3) x²-7|x|+6=0
Если x≥0, то
x²-7x+6=0
По теореме Виета 
x₁+x₂=7
x₁*x₂=6
x₁=1
x₂=6
Если x≤0, то
x²+7x+6=0
По теореме Виета 
x₁+x₂=-7
x₁*x₂=6
x₁=-1
x₂=-6
Ответ: $$ x_1=б1; x_2=б6 $$

Решить уравнение: а) x²-6|x|+5=0
б) (2х-1)^4-(2x-1)²-12=0

Подскажите действия решения вот этих уравнении:
1) y = √x+4 (х+4 здесь под корнем, а то символов нет)
2) lx^2 -10l > 9х (это модуль и там икс в квадрате)

$$ y= \sqrt{x+4} \\ y^{2}=x+4 \\ x=y^2-4 \\ |x^2-10|>9x \\ x^2-9x-10>0 \\ D=121 \\ x_1=10 $$
очевидно, что учловие выполняется только при значениях х принадлежащих промежутку ]10;+ ∞[
$$ x_2=-1 $$