модуль »

уравнение модуль х - страница 6

  • Решить уравнения: 1)/3-0.5х/=6+х

    2) /2х-4/-х=/х-3/+2 (//-модуль)


    Решение: 1) 3-x/2=6+x

        3/2x=-3

    x=-2  3-1/2x>=0  3>=x/2  x<=6

    x/2-3=6+x

    -9=x/2  x=-18    x>6

    x=2

    2) x=2 x=3

    x>3

    2x-4-x=x-3+2

    x-4=x-1

    -4=-1 решения нет

    x<2

    4-2x-x=3-x+2

    4-2x=5

    x=-1/2

    2<=x<=3

    2x-4-x=3-x+2

    2x-4=5

    x=4,5

    нет решения

    ответ х=-1/2

    $$ |3-0.5x|=6+x \\ \left \{ {{3-0.5x=6+x, x<6} \atop {0.5x-3=6+x, x>6}} \right. \\ \left \{ {{-1.5x=3, x<6} \atop {-0.5x=9, x>6}} \right. \left \{ {{x=-2, x<6} \atop {x=-18, x>6}}\right. \\ x=-2 $$

    Ответ: -2

    $$ |2x-4|-x=|x-3|+2 \\ \begin{cases} 4-2x-x=3-x+2, x < 2 \\ 2x-4-x=3-x+2, 2 < x3 \end{cases} \\ \begin{cases} -2x=1, x < 2 \\ 2x=9, 2 < x3 \end{cases} \\ \begin{cases} x=-0.5, x < 2 \\ x=4.5, 2 < x3 \end{cases} \\ x=-0.5 $$

    Ответ: -0,5

  • Решить уравнение: //х/+2/=7 Знаки /=модуль


    Решение: ││х│+2│=7              

    │х│+2=7              │х│+2=-7

                               │х│=-7-2

                               │х│=-9

    │х│=7-2                хпринадлежит пустому множеству

    │х│=5

    х+5

    х=-5

    ответ х=5;-5; х принадлежит пустому множеству

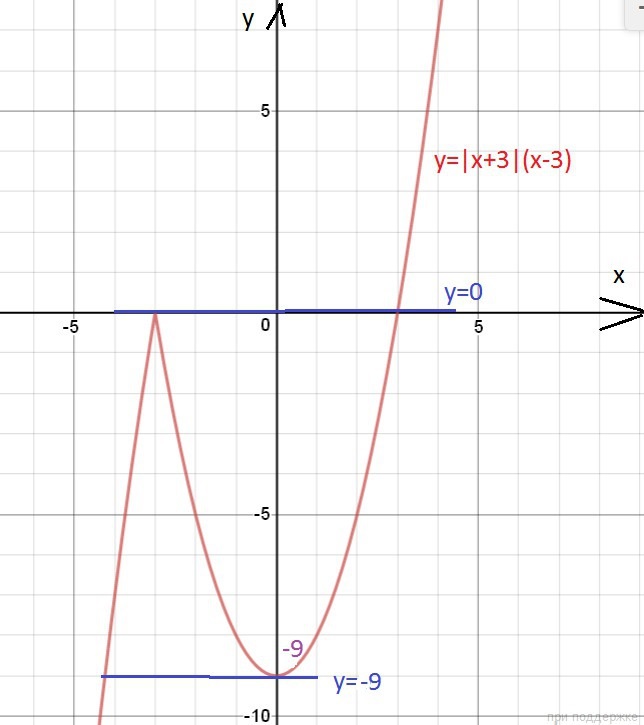
  • Найти мах целое значение параметра а при котором уравнение имеет 2 корня
    [x+3](x-3) разделить на а-3 =1
    х+3 под знаком модуль


    Решение: Запишем уравнение в виде
    |x+3|(x-3)=a-3
    а≠3
    Строим график функции
    у=|x+3|(x-3)
     
    На (-∞;-3)
    |x+3|=-x-3
    cтроим график у=-х²+9
    на [-3;+∞)
    |x+3|=x+3
    строим график у=х²-9
    График функции  у=a-3   при разных значения а - прямые, параллельные оси ох.
    Графики такого вида пересекаются с графиком у=|x+3|(x-3) в двух точка только в двух случаях
    a-3=0, но по условию а≠3
    или
    a-3=-9  ⇒  а=-6
    О т в е т. при а = - 6
     

    Запишем уравнение в виде x x- a- а Строим график функцииу x x-  На - - x -x- cтроим график у -х на - x x строим график у х - График функции  у a-    при разных значения а - п...

  • Х{х}=4 в середине это модуль надо найти корень уравнении


    Решение: Хх=4
    х²=4
    х=2 х=-2
    .

    Рассматриваем совокупность двух систем:
    $$ \left \{ {{x\ < \ 0} \atop {x*(-x)=4}} \right. \left \{ {{x \geq 0} \atop {x*x=4}} \right. \\ \left \{ {{x\ < \ 0} \atop { -x^{2} =4}} \right. \left \{ {{x \geq 0} \atop { x^{2} =4}} \right. \\ \left \{ {{x\ < \ 0} \atop { x^{2} =-4}} \right. \left \{ {{x \geq 0} \atop { x^{2} =4}} \right. $$
    Видим, что первая система не имеет решений, так как квадрат числа не может иметь отрицательное значение.
    Если решить вторую систему, то видим, что корнем данного уравнения является только 2. (Вообще х²=4 имеет два корня 2 и -2, но поскольку в системе также имеется неравенство х≥0, второй корень исключается, так как не является решением этого неравенства).
    Ответ: 2.

  • Решить уравнения с модулем
    /5х-2/-3=0 /7х-6/=/5-х/ /2х-1/+2=0 /-модуль


    Решение: 1) /5х-2/-3=0
    а) Раскроем положительный модуль: 5х-2-3=0, 5х=5, х=1
    б) Раскроем отрицательный модуль: -5х+2-3=0,5х=1, х=-1/5
    2) /7х-6/=/5-х/
    а) Оба модуля-положительны: 7х-6=5-х, 8х=11, х=11/8
    б) Оба модуля отрицательны: -7х+6=-5+х,8х=-11, х=11/8
    3) 1 модуль положительный, 2-отрицательный: 7х-6=-5+х, 6х=1, х=1/6
    4) 1 модуль-отрицательный, 2-положительный: -7х+6=5-х,6х=-1, х=1/6
    Ответ: 1/6; 11/8

<< < 456 7 > >>