модуль »

модуль разности квадратов

  • 1) Можно ли разрезать квадрат разрезать на две части так, чтобы части составляли 1/2 и 3/8 квадрата?
    2) Являются ли взаимно обратными модули взаимно обратных дробей?
    3) Может ли при сложении трёх дробей получиться сумма, меньшее каждого из слагаемых?


    Решение: 1) приведем дроби к одному знаменателю. То есть во второй дроби и числитель и знаменатель умножаем на 4. В итоге у нас дроби 4/8 и 3/8. При сложении они целого не дают 7/8 не равно 8/8 не равно 1)
    Ответ: нельзя.
    2) рассмотри на примере.
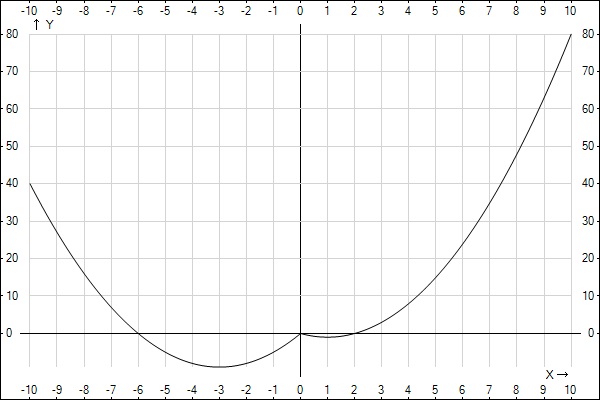
    3) тут тоже на примере. Да и чисто из логики. Если ты складываете 1/2 пирога с 1/8 у тетя всяко больше будет.

  • как построить график y=x’-4IxI+2x (игрик ровняется икс в квадрате минус четыре модуль икс плюс два икс)


    Решение: y=-x^2+4x при x=>0

    y=-x^2-2x при x<0

    Вот примерное графическое построение. Просто берётся любая точка и подставляется. Должно так выйти

    y -x x при x y -x - x при x...

  • y=x2-(x)-2
    x2-это икс в квадрате ; (х)- это модуль икс


    Решение: Уберём знак модуля, и рассмотрим оба случая:
    х2 - х - 2 = 0
    х2 + х - 2 = 0
    Получаем совокупность (не систему!) из двух обычных квадратных уравнений. Решаем их оба, как учили, любым способом. Получаем для первого корни -1 и 2, для второго -2 и 1.
    Проверим теперь все четыре корня на верность подстановкой в исходное уравнение с модулем, и видим, что -1 и 1 не подходят - тогда забываем про них. А вот -2 и 2 подходят - их пишем в ответ.

  • а)|х+у-2|+х^2-2ху+у^2=0

    б)|х-у-3|+х^2-4ху+4у^2=0

    (прямые палочки - модуль)

    (а значок ^2 - в квадрате)


    Решение: Первое переписывается в виде |x+y-2|+(x-y)^2=0, второе - |x-y-3|+(x-2y)^2=0.

    Везде слагаемые неотрицательны, чтобы сумма была равной нулю необходимо, чтобы каждое слагаемое равнялось нулю.

    а) Из первого слагаемого получаем x+y=2, из второго x=y. Решая несложную систему, получим x=y=1.

    б) Из первого слагаемого x=y+3, из второго х=2у. Подставляя х из первого, получаем у+3=2у, откуда у=3, х=6.

  • Определить модуль силой F, которую нужно приложить к деревянному бруска массой 2 кг, под углом 30 градусов вертикально, чтобы он двигался вдоль вертикальной стены с ускорением 0,2 м в сек в квадрате коэффициент трения между бруском и стеной =0,5


    Решение: Дано
    m=2кг
    угол 30 гр
    а=0.2 м/с^2
    k=0.5
    -
    F-
    чертите рисунок ось 0х горизонтальная
    ось оу вертикальная
    по оси 0Х на брус действуют силы:
    Fsin(30)-N=0
    n=Fsin(30)
    по оси 0Y на брус действуют силы:
    Fcos(30)-kN-mg=ma
    Fcos(30)-kFsin(30)=ma+mg
    F(cos(30)-ksin(30))=m(а+g)
    F=m(a+g)/(cos(30)-ksin(30))=2*10(0.86-0.25)=12.2 Н
    Ответ: 12.2 Н

  • Докажите, что модуль разности квадратов двух последовательных нечетных натуральных чисел равен удвоенной сумме этих чисел


    Решение: Пусть x - одно чётное число, тогда второе будет x+2. Согласно утверждению, получаем (x+2)^2-x^2=2(x+2+x), т. е. (x+2)^2-x^2 = 2(2x+2). Проверим это утверждение.
    (x+2)^2-x^2=(x+2-x)(x+2+x)=2(2x+2). Что и требовалось доказать)

    А-нечетное число
    а+2-второе нечётное число
    модуль(а+2)^2-a^2=(a+2)^2-a^2=a^2+4a+4-a^2=4a+4=2(a+(a+2)) чтд

  • При каких значениях а модуль разности квадратов корней трехчлена (а+1)*х^2+(a+3)*x-4a-4 равен 15


    Решение: $$ |x_1^2-x_2^2|=15 $$ тогда и только тогда, когда
    $$ (x_1^2-x_2^2)^2=(x_1-x_2)^2(x_1+x_2)^2=((x_1+x_1)^2-4x_1x_2)(x_1+x_2)^2=15^2. $$ Обозначим через t сумму корней. По т. Виета $$ t=x_1+x_2=-(a+3)/(a+1), $$ $$ x_1x_2=-(4a+4)/(a+1)=-4. $$ Таким образом, $$ (t^2+16)t^2=15^2 $$. Отсюда $$ t^2=9 $$ и $$ t^2=-25, $$ т. е. $$ t=\pm 3. $$ Значит, из условия $$ t=-(a+3)/(a+1)=\pm3 $$ находим  a=-3/2 и a=0. В обоих случаях дискриминант уравнения положителен, т. е. имеются  2 действительных корня, поэтому ответ a=-3/2 и a=0.

    Во-первых, а =/= -1, потому что иначе коэффициент при x^2 будет = 0.
    Во-вторых, решаем уравнение
    (a+1)*x^2 + (a+3)*x + (-4a-4) = 0
    Можно решить традиционным способом
    D = (a+3)^2 - 4(a+1)(-4a-4) = (a+3)^2 + 16(a+1)^2 =
    = a^2 + 6a + 9 + 16a^2 + 32a + 16 = 17a^2 + 38a + 25 > 0 при любом а.
    x1 = (-a-3 - √(17a^2 + 38a + 25)) / (2a+2)
    x2 = (-a-3 + √(17a^2 + 38a + 25)) / (2a+2)
    Но в принципе это все неважно. Рассмотрим модуль разности
    |x1^2 - x2^2| = |(x1 - x2)(x1 + x2)| = 15
    Denik777 навел меня на мысль. Разность квадратов корней нужно возвести в квадрат.
    (x1^2 - x2^2)^2 = (x1 - x2)^2 * (x1 + x2)^2 = 15^2 = 225
    (x1^2 - 2x1*x2 + x2^2)(x1 + x2)^2 = 225
    (x1^2 + 2x1*x2 + x2^2 - 4x1*x2)(x1 + x2)^2 = 225
    ((x1 + x2)^2 - 4x1*x2)(x1 + x2)^2 = 225
    По теореме Виета x1 + x2 = -(a+3)/(a+1); x1*x2 = (-4a-4)/(a+1) = -4
    ((a+3)^2/(a+1)^2 - 4(-4))*(a+3)^2/(a+1)^2 = 225
    ((a+3)^2 + 16(a+1)^2)*(a+3)^2 / (a+1)^4 = 225
    Первая скобка равна D, который мы уже вычислили
    (17a^2 + 38a + 25)(a^2 + 6a + 9) = 225(a + 1)^4
    17a^4+38a^3+25a^2+102a^3+228a^2+150a+153a^2+342a+225 =
    = 225a^4 + 900a^3 + 1350a^2 + 900a + 225
    Упрощаем
    208a^4 + 760a^3 + 944a^2 + 408a = 0
    Делим на 8
    26a^4 + 95a^3 + 118a^2 + 51a = 0
    a1 = 0
    26a^3 + 95a^2 + 118a + 51 = 0
    Кубическое уравнение имеет как минимум 1 корень.
    И в данном случае отрицательный. При a > 0 корней явно нет.
    F(-3) = -150 < 0; F(-2) = -13 < 0; F(-1) = 2 > 0
    -2 < a2 < -1
    Можно уточнить, например до точности 0,1
    F(-1,4) = -26*1,4^3 + 95*1,4^2 - 118*1,4 + 51 = 0,656 > 0
    F(-1,5) = -26*1,5^3 + 95*1,5^2 - 118*1,5 + 51 = 0
    a2 = -1,5

  • Сумма двух чисел равна 18, а их произведение 61. Найдите модуль разности квадратов этих чисел


    Решение: По т еореме Виета мы знаем, чему равна сумма и произведение корней кв. уравнения. Составим это уравнение и найдём его корни.
    $$ x^2+px+q=0\; \; \; x_1\cdot x_2=q,\; x_1+x_2=-p\\\\ \left \{ {{x_1\cdot x_2=61} \atop {x_1+x_2=18}} \right. \; \to \; q=61,\; p=-18\\\\x^2-18x+61=0\\\\D=324-244=80,\; \sqrt{D}=\sqrt{80}=4\sqrt5\\\\x_1=\frac{18-4\sqrt5}{2}=9-2\sqrt5\\\\x_2=9+2\sqrt5 $$
    Проверку можно сделать самому, сложить и умножить оба числа.

  • Доказать, что если каждое из двух натуральных чисел не делится на 3, то модуль разности квадратов этих чисел делится на 3


    Решение: Пусть даны два натуральных числа A и B. Тогда по условию:
    A = 3p+r1;
    B = 3q+r2;
    r1 и r2 могут принимать значения 1 и/или 2, и только (т. е. других значений, кроме 1, 2 принимать не могут).
    Модуль разности квадратов этих чисел делится на 3, если разность квадратов делится на 3. (Значение и модуль этого значения отличаются лите знаком, либо же вообще не отличаются).
    A^2 - B^2 = (3p+r1)^2 - (3q+r2)^2 = (9*p^2) + 6p*r1 + r1^2 - (9*q^2) - 
    - 6q*r2 - r2^2 = 3*(.) + r1^2 - r2^2.
    Посмотрим какие значения может принимать R=(r1^2 - r2^2), при условиях данных в задаче. Для этого составим таблицу.
    r1=1; r2=1; R=0;
    r1=1; r2=2; R=1 - 4 = -3;
    r1=2; r2=1; R=4-1=3;
    r1=2; r2=2; R= 4-4 = 0;
    Во всех случаях (при условии задачи) R делится нацело на 3, т. е. R=3*r; поэтому
    A^2 - B^2 = 3*(.) + 3*r = 3*(. + r).
    очевидно делится на 3.

  • |sqrt|(x-2|-1|=a
    Визначте кількість коренів залежно від значення параметра a
    sqrt - это корень квадратный
    | | - модуль


    Решение: Если правильно поняла ваше условие:
    $$ | \sqrt{|x-2|}-1|=a $$
    если а<0, то уравнение корней не имеет, поскольку модуль - число всегда неотрицательное.
    если a≥0
    Тогда модуль можно раскрыть двумя случаями:
    1й случай
    $$ \sqrt{|x-2|}-1=a $$
    $$ \sqrt{|x-2|}=a+1 \\ |x-2|=(a+1)^2 \\ x-2=(a+1)^2 $$ или $$ x-2=-(a+1)^2 $$ 
    $$ x_{1}=(a+1)^2+2=a^2+2a+3 $$ $$ x_{2}=2-(a+1)^2=-a^2-2a+1 $$
    2й случай
    $$ \sqrt{|x-2|}-1=-a $$
    $$ \sqrt{|x-2|}=1-a $$
    снова идет ветвление на два случая:
    если а∈[0;1], то получаем следующее:
    $$ \sqrt{|x-2|}=1-a \\ |x-2|=(1-a)^2 \\ x-2=(1-a)^2 $$ или $$ x-2=-(1-a)^2 $$ 
    $$ x_{1}=(1-a)^2+2=a^2-2a+3 $$ $$ x_{2}=2-(1-a)^2=-a^2+2a+1 $$
    То есть, уравнение имеет два корня.
    если а∈(1;+∞), то получаем, что уравнение корней не имеет, поскольку значение корня квадратного - всегда неотрицательное, а при любом а их данного промежутка правая часть будет отрицательной.
    Ответ:
    при a∈(-∞;0)∨(1;+∞) уравнение не имеет корней
    при а∈[0;1] уравнение имеет два корня: $$ x_{1}=(1-a)^2+2 $$ $$ x_{2}=2-(1-a)^2 $$

1 2 > >>