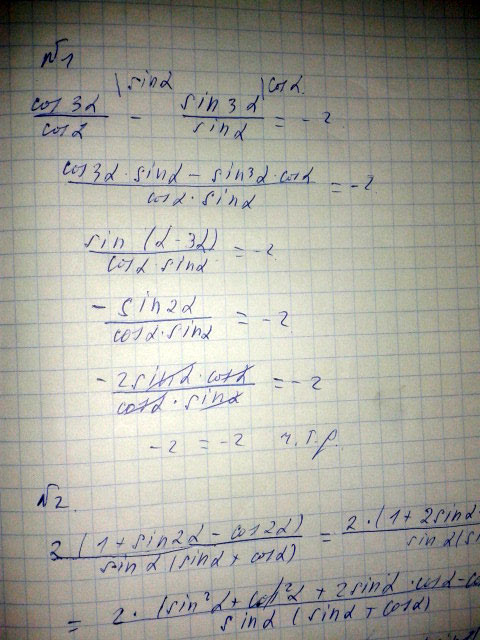тождество »

докажите тождество - страница 39

  • Докажите тождество \( \frac{sin2\alpha + cos(\pi-\alpha)sin\alpha}{sin(\frac{\pi}{2}-\alpha)} \) и упростите выражение \( (\frac{cos2\alpha}{sin\alpha-cos\alpha})^2 - sin2\alpha \)


    Решение: COS(π-α)= - COS(α), SIN(π/2-α)=COS(α), SIN(2α)=2SIN(α)COS(α)
    [SIN(2α)+COS(π-α)SIN(α)]/SIN(π/2-α)=[2SIN(α)COS(α)-COS(α)SIN(α)]/COS(α) = SIN(α)COS(α)/COS(α) = SIN(α)
    2) COS(2α) / (SIN(α)-COS(α))↑2-SIN(2α)
    COS(2α) = COS²(α) - SIN²(α) = (COS(α) - SIN(α) )·(COS(α) + SIN(α) )
    [COS(2α)/( SIN(α) - COS(α))]²-SIN(2α) =
    =[ (COS(α) - SIN(α) )·(COS(α) + SIN(α) )/(SIN(α) -COS(α)) ]²-
    -2COS(α) SIN(α)=
    = COS²(α) + 2COS(α)SIN(α) +SIN²(α)-2COS(α) SIN(α)=
    =COS²(α) +SIN²(α)=1

  • Докажите тождество \( \frac{cos3\alpha}{cos\alpha}-\frac{sin3\alpha}{sin\alpha}=-2 \)
    Упростите выражение \( \frac{2(1+sin2\alpha-cos\alpha)}{sin\alpha(sin\alpha+cos\alpha)} \)


    Решение: $$ \frac{cos3\alpha}{cos\alpha}-\frac{sin3\alpha}{sin\alpha}=-2\ \ \ \ \ \ \ \ \ \ \ \ |*(cos\alpha * sin\alpha)\\cos3\alpha*sin\alpha-sin3\alpha*cos\alpha=-2cos\alpha*sin\alpha\\-(sin3\alpha*cos\alpha-cos3\alpha*sin\alpha)=-sin2\alpha\\-sin(3\alpha-\alpha)=-sin2\alpha\\-sin2\alpha=-sin2\alpha \\ \frac{2(1+sin2\alpha-cos\alpha)}{sin\alpha(sin\alpha+cos\alpha)}=\\=\frac{2(sin^2\alpha+cos^2\alpha+2sin\alpha*cos\alpha-(cos^2\alpha-sin^2\alpha))}{sin\alpha(sin\alpha+cos\alpha)}=\\=\frac{2(2sin^2\alpha+2sin\alpha*cos\alpha)}{sin^2\alpha+sin\alpha*cos\alpha}=\frac{2*2(sin^2\alpha+sin\alpha*cos\alpha)}{sin^2\alpha+sin\alpha*cos\alpha}=4 $$ 

    $$ cos75а=cos(45а+30а)=cos45а*cos30а-sin45а*sin30а=\\=\frac{\sqrt{2}}{2}*\frac{\sqrt{3}}{2}-\frac{\sqrt{2}}{2}*\frac{1}{2}=\frac{\sqrt{6}-\sqrt{2}}{4}=\frac{\sqrt{2}(\sqrt{3}-1)}{4} $$ 

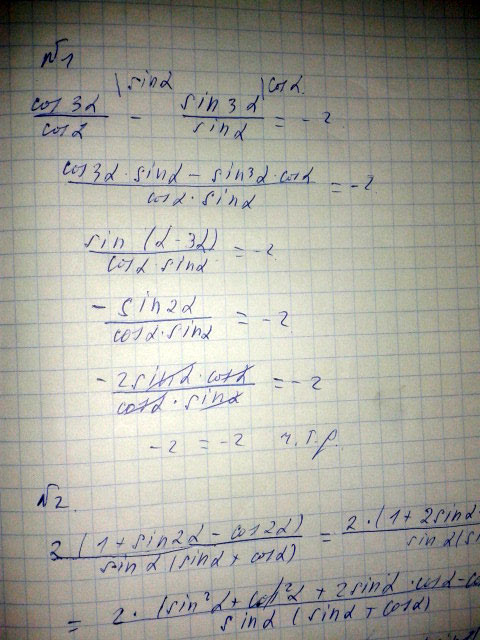
    frac cos alpha cos alpha - frac sin alpha sin alpha - cos alpha sin alpha cos alpha sin alpha-sin alpha cos alpha - cos alpha sin alpha - sin alpha cos alpha-cos alpha sin al...

  • 1. Упростите выражение :
    ((x/y) + (y/x)) умножить на (x^2y^2/x^2+y^2) - xy
    2. Упростите выражение:
    ((2ab/a^3-b^3)+(a-b/a^2+ab+b^2)):a^2+b^2/a-b
    3. Докажите тождество:
    ((1/x)-(1/x^2)) : ((x-1)/x) - (1/x)+(x/x-2) - (x/x+2) = 4x/x^2-4


    Решение: 1. Упростите выражение :
    $$ (\frac{x}{y}+\frac{y}{x})(\frac{x^2y^2}{x^2+y^2})-xy \\ \\ 1) \frac{x}{y}+\frac{y}{x}= \frac{x^2+y^2}{xy} \\ \\ 2) \frac{x^2+y^2}{xy}*\frac{x^2y^2}{x^2+y^2}=xy \\ \\ 3) xy-xy=0 $$
    2. Упростите выражение:
    $$ (\frac{2ab}{a^3-b^3}+\frac{a-b}{a^2+ab+b^2}):\frac{a^2+b^2}{a-b} \\ \\ 1) \frac{2ab}{a^3-b^3}+\frac{a-b}{a^2+ab+b^2}= \frac{2ab}{(a-b)(a^2+ab+b^2)}+\frac{a-b}{a^2+ab+b^2}= \\ \\ =\frac{2ab+(a-b)^2}{(a-b)(a^2+ab+b^2)}=\frac{2ab+a^2-2ab+b^2}{(a-b)(a^2+ab+b^2)}=\frac{a^2+b^2}{(a-b)(a^2+ab+b^2)} \\ \\ 2) \frac{a^2+b^2}{(a-b)(a^2+ab+b^2)}:\frac{a^2+b^2}{a-b}=\frac{a^2+b^2}{(a-b)(a^2+ab+b^2)}*\frac{a-b}{a^2+b^2}= \\ \\ =\frac{1}{a^2+ab+b^2} $$
    3. Докажите тождество:
    $$ (\frac{1}{x}-\frac{1}{x^2}):\frac{x-1}{x}-\frac{1}{x}+\frac{x}{x-2}-\frac{x}{x+2}=\frac{4x}{x^2-4} \\ \\ 1) \frac{1}{x}-\frac{1}{x^2}= \frac{x-1}{x^2} \\ \\ 2) \frac{x-1}{x^2}:\frac{x-1}{x}=\frac{x-1}{x^2}*\frac{x}{x-1}= \frac{1}{x} \\ \\ 3) \frac{1}{x}-\frac{1}{x}+\frac{x}{x-2}-\frac{x}{x+2}=\frac{x}{x-2}-\frac{x}{x+2}=\\= \frac{x(x+2)-x(x-2)}{(x-2)(x+2)} =\frac{4x}{x^2-4} $$

  • 1. упростите выражение
    а) (3x^2 +y)(2y-5x^2)
    б) (7x-1)(x^2-4x+2)
    в) (a^2+b^2)(2a-b)-ab(b-a)
    г) -8p(p+3)(2-p^2)
    2. разложите на множители
    а) 2x^5 +5x^4-2x^2-5x
    б) 3a-3b+(a-b)^2
    3. Докажите тождество
    x^5+1=(x+1)(x^4-x^3+x^2-x+1)
    цифра после ^ обозначает степень


    Решение: 1. упростить выражение
    а) (3x^2 +y)(2y-5x^2)=6x²y-15x^4+2y²-5x²y=x²y-15x^4+2y²
     б) (7x-1)(x^2-4x+2)=7x³-28x²+14x-x²+4x-2=7x³-29x²+18x-2
    в) (a^2+b^2)(2a-b)-ab(b-a)=2a³-a²b+2ab²-b³-ab²+a²b=2a³+ab²-b³
    г) -8p(p+3)(2-p^2)=(-8p²-24p)(2-p²)=-16p²+8p^4-48p+24p³
    2. разложите на множители
    а) 2x^5 +5x^4-2x^2-5x=2x²(x³-1)+5x(x³-1)=(x³-1)(2x²+5x)=x(2x+5)(x-1)(x²+x+1)
    б) 3a-3b+(a-b)^2=3(a-b)+(a-b)(a+b)=(a-b)(3+a+b)
    3. Докажите тождество
    x^5+1=(x+1)(x^4-x^3+x^2-x+1)
    (x+1)(x^4-x^3+x^2-x+1)=x^5-x^4+x³-x²+x+x^4-x³+x²-x+1=x^5+1
    x^5+1=x^5+1

  • №1 Докажите, что выражение принимает лишь положительное значение:
    a^2+b^2+c^2-2bc+3
    №2 Представьте в виде произведения:
    m^3-m^2n-mn^2+n^3
    №3 Докажите тождество:
    (a^4+b^4)(a^2+b^2)(a+b)(a-b)=a^8b^8
    №4 Разложите на множители:
    1)a^4-b^4
    2)a^8-b^8


    Решение: Номер 1
    a^2+b^2+c^2-2bc+3 = a²+3+ (b+c)² 
    сумма квадратов это число положительное, и оно остается положительным, если прибавить 3
     номер 2
    m^3-m^2n-mn^2+n^3=m(m²-n²) -n(m²-n²)=(m-n)²(m+n)
    номер 3
    (a^4+b^4)(a^2+b^2)(a+b)(a-b)=(a^4+b^4)(a²+b²)(a²-b²)=(a^4+b^4)(a^4-b^4)=a^8-b^8
    номер 4
    1)a^4-b^4= (a²-b²)(a²+b²)=(a-b)(a+b)(a²+b²)
    2)a^8-b^8=(a^4+b^4)(a^2+b^2)(a+b)(a-b

<< < 373839 40 41 > >>