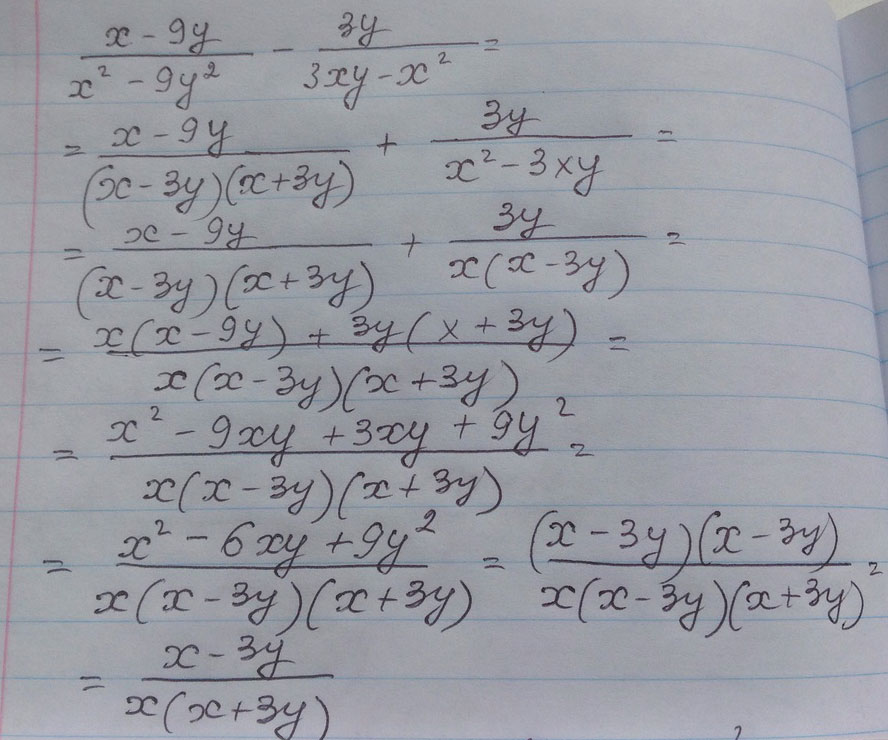докажите тождество - страница 38
Упростите выражения : х-9у/х^2-9у^2-3у/3ху-х^2
Упростите выражение : 7b-4a-28/7b-4ab+20a-35- 7/7-4a и найдите его значение при a=0,1115;b=2,5
Докажите тождество : 4/а^2-4а-а^2/4-а=а+4+16а+4/а^2-4а
Решение: 1)(x-9y)/(x-3y)(x+3y) +3y/x(x-3y)=(x²-9xy+3xy+9y²)/(x(x²-9y²)=(x²-6xy+9y²)/(x²-9y²)=
=(x-3y)²/(x-3y)(x+3y)=(x-3y)/(x+3y)
3)4/a(a-4)+a²/(a-4)=((4+a³)/a(a-1)=(a³+4)/(a²-4a)
(a+4)+(16aa+4)/(a²-4a)=(a³+4a²-4a²-16a+16a+4)/(a²-4a)=(a³+4)/(a²-4a)
(a³+4)/(a²-4a)=(a³+4)/(a²-4a)
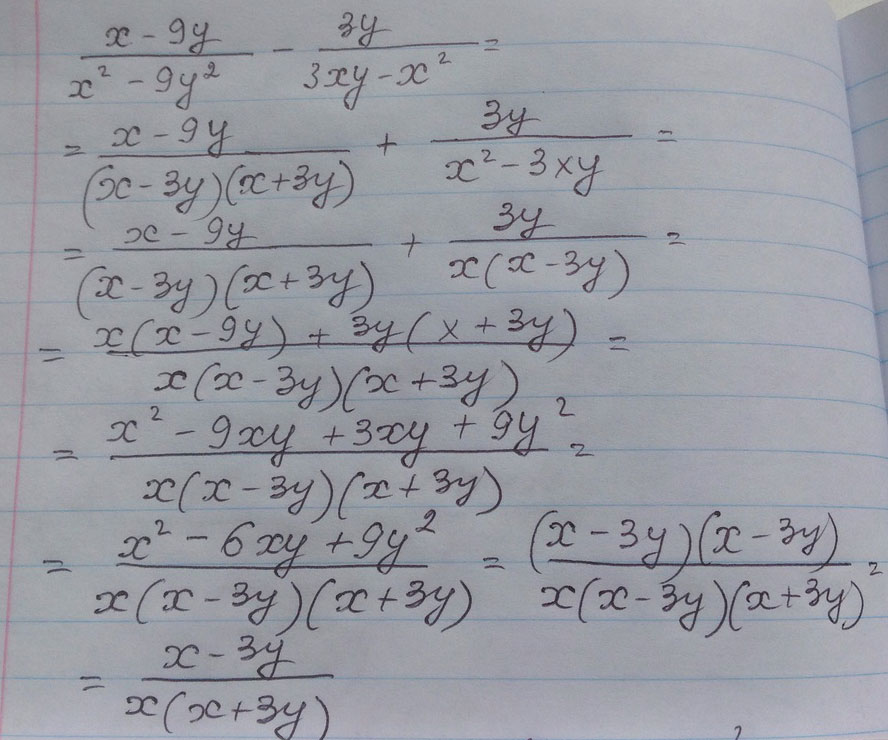
1) Упростите выражения:
(3x^2+y)(2y-5x^2)
(7x-1)(x^2-4x+2)
(a^2+b^2)(2a-b)-ab(b-a)
-8b(b+3)(2-b^2)
2) Разложите на множители:
2x^5+5x^4-2x^2-5x
3a-3b+(a-b)^2
3) Докажите тождество:
x^5+1=(x+1)(x^4-x^3+x^2-x+1)
4) Представьте в виде произведения:
x^2-2xy+x-xz+2yz-z
a^3-ab-a^2b+a^2
Решение: 1)(3x^2+y)(2y-5x^2)=6x^2y-15x^4+2y^2-5x^2y=-15x^4+x^2y+2y^2(7x-1)(x^2-4x+2)=7x^3-28x^2+14x-x^2-4x-2=7x^3-29x^2+18x-2
(a^2+b^2)(2a-b)-ab(b-a)=2a^3-a^2b+2ab^2-b^3-ab^2+a^2=2a^3-b^3-a^2b+ab^2+a^2
-8b(b+3)(2-b^2)=-8b(2b-b^3+6-3b^2)=-16b^2+8b^4-48b+24b^3=8b^4+24b^3-16b^2-48b
2)2x^5+5x^4-2x^2-5x=2x^5-2x^2+5x^4-5x=2x^2(x^3-1)+5x(x^3-1)=(2x^2-1)(x^3-1)
3a-3b+(a-b)^2=3(a-b)+(a-b)^2=(3+a-b)(a-b)
3)x^5+1=(x+1)(x^4-x^3+x^2-x+1)
(x+1)(x^4-x^3+x^2-x+1) = x^5-x^4+x^3-x^2+x+x^4-x^3+x^2-x+1=x^5+1
Разложите на множители:
а) 25х – х³
б) 2х² – 20х + 50
3. Найдите значение выражения а² – 4bс, если а = 6, b = -11, с = -10
4. Упростите выражение: (с² – b)² – (с² + 1)² + 2bс²
5. Докажите тождество: (а + b)² – (а – b)² = 4аb
Решение: Применяем способы разложения на множители. Сначала выносим общий множитель х, потом по формуле разности квадратов a²-b²=(a-b)(a+b)
а) 25х – х³=х·(25-х²)=х·(5-х)·(5+х)
б) 2х² – 20х + 50=2(x²-10x+25)=2(x-5)²
Сначала выносим за скобку 2, далее по формуле
(a-b)²=a²-2ab+b²
3. Найдите значение выражения а² – 4bс, если а = 6, b = -11, с = -10
6²-4·(-11)·(-10)=36-440=-404
4. Упростите выражение: (с² – b)² – (с² + 1)² + 2bс²=с⁴-2с²b+b²-(c⁴+2c²+1)+2bc²=с⁴-2с²b+b²-c⁴-2c²-1+2bc²=b²-2c²-1
5. Докажите тождество: (а + b)² – (а – b)² = 4аb
(а + b)² – (а – b)² = a²+2ab+b²-(a²-2ab+b²)=a²+2ab+b²-a²+2ab-b²=4ab
4ab=4ab
Разложить на множители: а) y^3 - 49y
Найдите значение выражения a^2 - 4bc, если a = 6, b = -11, c = -10
Упростите выражения: (a - 1)^2 (a + 1) + (a + 1)( a - 1)
Докажите тождество: (x - y)^2 + (x + y)^2 = 2(x^2 + y^2)
Решение: разложить на множители:а) сначала выносим у
у(у^2-49)=у((у-7)(у+7))
найдите значение выражения
а^2-4bc если а=6 в=-11 с=-10
сразу подставляем
6*6-4*(-11)*(-10)=36-440=-404
упростите выражения
= (а^2-1)^2+а^2-1= а^4-2а^2+1+а^2-1 = а^4-а^2
докажите тождество
х^2-2ху+у^2+х^2+2ху+у^2=2х^2+2у^2
упрощаем
2х^2+2у^2=2х^2+2у^2
вроде так!
a) y^3-49y=y(y^2-49)=y(y-7)(y+7)
b) -3a^2-6ab-3d^2=-3(a^2+2ab+d^2)=-3(a+d)^2
(a-1)^2(a+1)+(a+1)(a-1)=(a-1)(a+1)(a-1)=(a+1)(a-1)^2
(x-y)^2+(x+y)^2=x^2-2xy+y^2+x^2+2xy+y^2=2x^2+2y^2=2(x^2+y^2)
1) Упростите выражение \( 1.\;a)\;\sin(\alpha-\beta)+\cos\alpha\sin\beta\\b)\;\frac12\sin\alpha+\cos\left(\frac\pi6+\alpha\right)\)
2) Докажите тождество \( \cos(\alpha+\beta)+\cos(\alpha-\beta)=2\cos\alpha\cos\beta \)
Решение: $$ 1.\;a)\;\sin(\alpha-\beta)+\cos\alpha\sin\beta=\sin\alpha\cos\beta-\cos\alpha\sin\beta+\cos\alpha\sin\beta=\\=\sin\alpha\cos\beta\\b)\;\frac12\sin\alpha+\cos\left(\frac\pi6+\alpha\right)=\frac12\sin\alpha+\cos\frac\pi6\cos\alpha-\sin\frac\pi6\sin\alpha=\\=\frac12\sin\alpha+\frac{\sqrt3}2\cos\alpha-\frac12\sin\alpha=\frac{\sqrt3}2\cos\alpha \\ 2)\;\cos(\alpha+\beta)+\cos(\alpha-\beta)=\\=\cos\alpha\cos\beta-\sin\alpha\sin\beta+\cos\alpha\cos\beta+\sin\alpha\sin\beta=2\cos\alpha\cos\beta $$