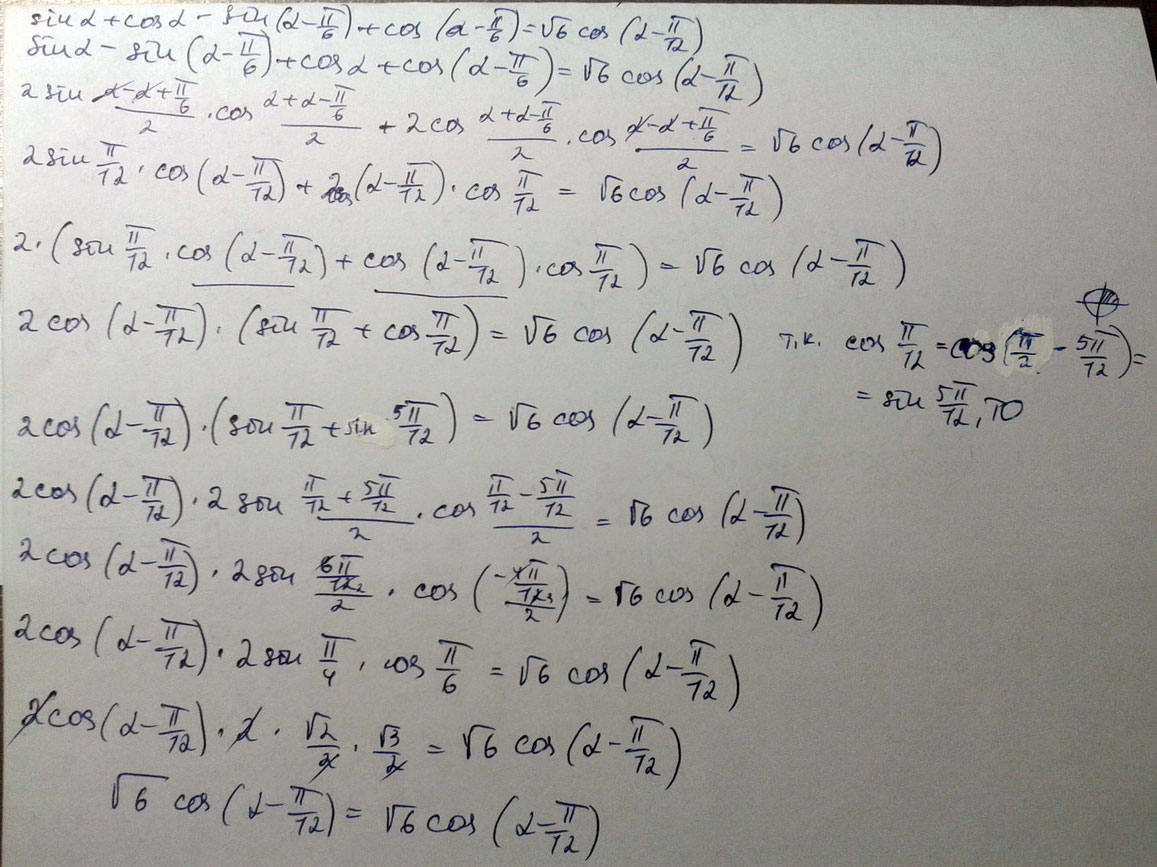тождество »
как доказать тождество - страница 34
ТРИГОНОМЕТРИЯ(тождество)
\( sin \alpha +cos \alpha -sin( \alpha -\frac{ \pi}{6} )+ cos(\alpha-\frac{\pi}{6})=\\= \sqrt{6}cos(\alpha-\frac{\pi}{12}) \)
Нужно доказать тождество
Решение: [sina-sin(a-π/6)]+[cosa+cos(a-π/6)]=
=2sin(π/12)cos(a-π/12)+2cos(π/12)cos(a-π/12)=
=2cos(a-π/12)*(sinπ/12+cosπ/12)=2cos(a-π/12)*(sinπ/12+sin5π/12)=
=2cos(a-π/12)*2sinπ/4*cosπ/6=4*√2/2*√3/2*cos(a-π/12)=√6cos(a-π/12)
√6cos(a-π/12)=√6cos(a-π/12)
Всё решаем по формулам.
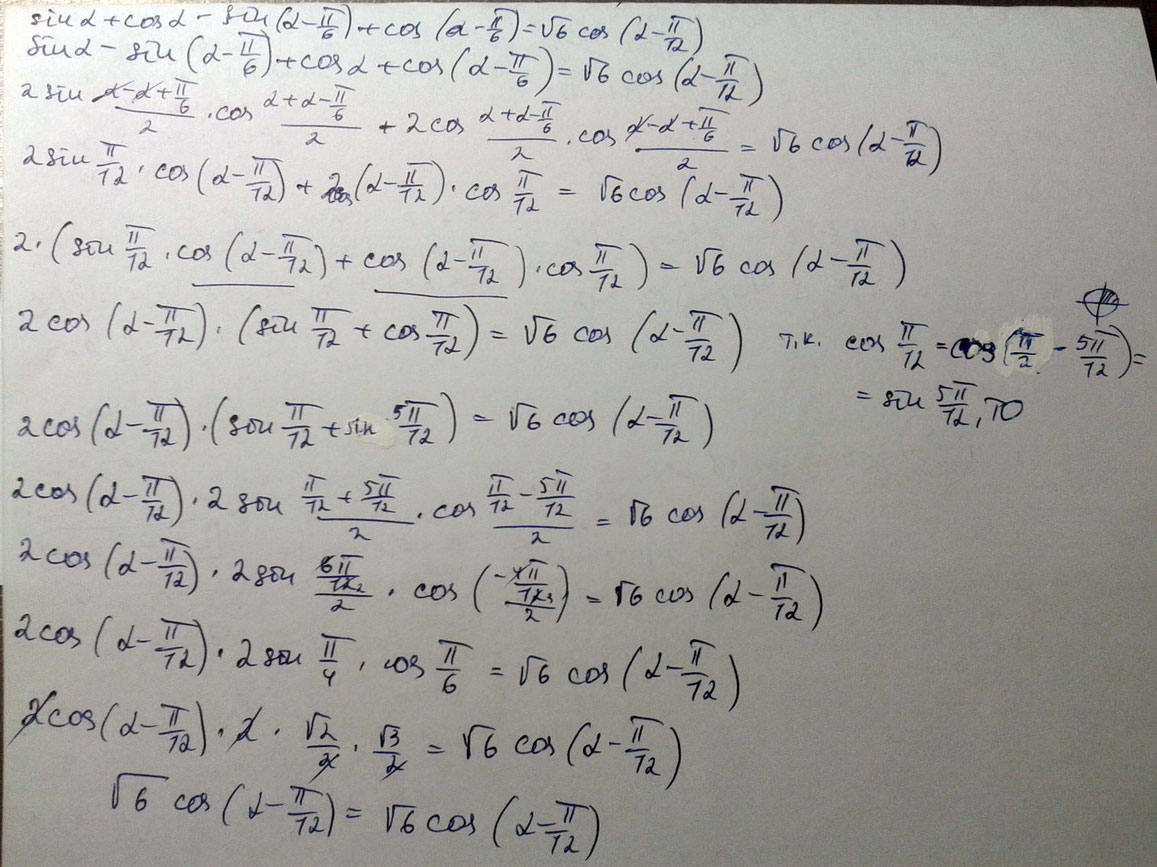
Доказать тождество \( \frac{(cos \alpha -sin \alpha ) ^{2}+(cos \alpha +sin \alpha ) ^{2} }{2} -sin ^{2} \alpha =\\=ctg \alpha * cos \alpha *sin \alpha \)
Решение: $$ (cos \alpha -sin \alpha) ^{2} +(cos \alpha+sin \alpha) ^{2} = cos^{2} \alpha -2cos \alpha sin \alpha + sin^{2} \alpha + \\ + cos^{2} \alpha +2cos \alpha sin \alpha + sin^{2} \alpha=2cos^{2} \alpha+2sin^{2} \alpha = 2(cos^{2} \alpha+sin^{2} \alpha)=2 \\ 2/2=1\\ 1-sin ^{2} \alpha =cos ^{2} \alpha \\ ctg \alpha = \frac{cos \alpha }{sin \alpha } \\ \frac{cos \alpha }{sin\alpha} *cos \alpha*sin \alpha=cos ^{2} \alpha \\ cos ^{2} \alpha =cos ^{2} \alpha $$ Доказано
Нужно доказать тождество:
подробно объясните (распишите)
а"4 - в"4 1
- = -
((а+в)"2-4ав)((а-в)"2-4ав)((а+в)"2-2ав) а"2 -в"2
Решение: (а+в)^2 - (а-в)^2=4ав, применяем формулу(а^2+2aв+в^2)-(a^2-2aв+в^2) Теперь раскрываем скобки, при этом во второй скобке знаки меняются на противоположные т. к. перед скобкой знак минусa^2+2aв+в^2-a^2+2aв-в^2=4aв, появились одинаковые множители с противоположными знаками, их вычеркиваем и остается:2ав+2ав=4ав, складываем 4ав=4ав ч. т. д.