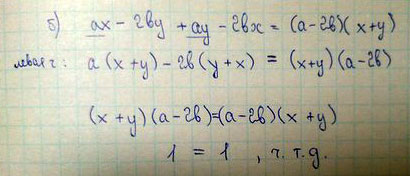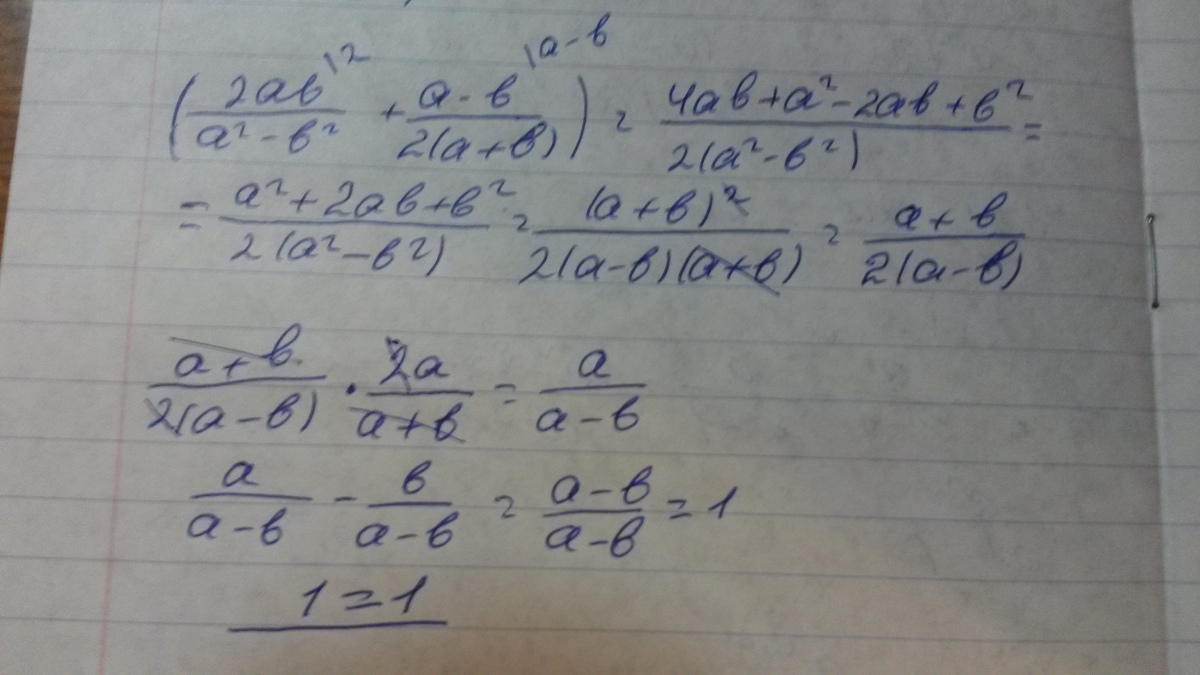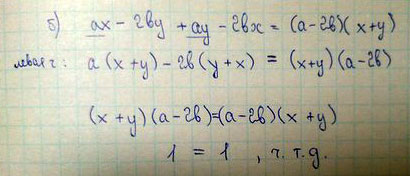тождество »
как доказать тождество - страница 32
Нужно доказать тождества: a) \( 1-tg^2 -\alpha=\frac{cos2\alpha}{cos^2\alpha} \)
b) \(ctg^2\alpha - 1=\frac{cos2\alpha}{sin^2\alpha} \)
Решение: А) В левой части тождества запишем тангенс как sin²(-α)/cos²(-α), так как синус и косинус в квадрате, то минусы у аргументов самоуничтожаются и останется sin²α/cos²α, тогда тождество перепишется в виде: 1-sin²α/cos²α=cos2α/cos²α,
приведем левую часть тождества к общему знаменателю, получим cos²α-sin²α/cos²α=cos2α/cos²α, выражение cos²α-sin²α является формулой двойного угла косинуса, то есть cos²α-sin²α=cos2α; тогда cos2α/cos²α=cos2α/cos²α. Тождество доказано.
б) Котангенс представим в виде cos²α/sin²α, тогда cos²α/sin²α-1=cos2α/sin²α,
левую часть приведем к общему знаменателю, получим cos²α-sin²α/sin²α=cos2α/sin²α. Далее, аналогично первому доказательству. cos2α/sin²α=cos2α/sin²α. Тождество доказаноДоказать тождество:
1. (а-2)^2-2а(а-2)+а^2=4
2. х^2-2х(х-3)+(х-3)^2=9
3. 5х(х-у)-2(у-х)^2=(3х+2у)(х-у)
4. (а-1)(а^2+1)(а+1)-(а^2-1)^2=2(а^2-1)
5. (а^2+1)^2+(а-1)(а^2+1)-а^2=а(а^3+а^2+1)
6. (х^2-1)(х^4+х^2+1)-(х^2-1)^3=3х^2(х^2-1)
Решение: 1.
$$ (a-2)^2-2a(a-2)+a^2=(a-2)(a-2-2a)+a^2= \\ =-(a-2)(a+2)+a^2=-a^2+4+a^2=4 $$
2,
$$ x^2-2x(x-3)+(x-3)^2=x^2-(2x-x+3)(x-3)= \\ =x^2-(x-3)(x+3)=x^2- x^{2} +9=9 $$
3.
$$ 5x(x-y)-2(y-x)^2=(y-x)(-5x-2(y-x))= \\ =(y-x)(-5x+2x-2y)=(x-y)(3x+2y) $$
4.
$$ (a-1)(a^2+1)(a+1)-(a^2-1)^2=(a^2-1)(a^2+1-a^2+1)= \\ =2(a^2-1) $$
5,
$$ (a^2+1)^2+(a-1)(a^2+1)-a^2=(a^2+1)(a^2+1+a-1)-a^2= \\ =(a^2+1)(a^2+a)-a^2=a^4+a^3+a^2+a-a^2=a(a^3+a^2+1) $$
6.
$$ (x^2-1)(x^4+x^2+1)-(x^2-1)^3=(x^2-1)(x^4+x^2+1-(x^2-1)^2)= \\ ( x^{2} -1)(x^4+x^2+1-x^4+2x^2-1)=3x^2(x^2-1) $$
Надо доказать тождество \( (\frac{2ab}{a^2 -b^2} + \frac{a-b}{2(a+b)})\cdot \frac{2a}{a+b}-\frac{b}{a-b}=1 \)
Решение: б) = (((4ab+(a-b)²)/2(a+b)(a-b)) *2a/(a+b) -b/(a-b) =
((a+b)²/2(a+b)(a-b)) *2a/(a+b) -b/(a-b) =a/(a-b) -b/(a-b) =(a-b)/(a-b) =1
-4ab+(a-b)² =4ab +a²-2ab+b² =a²+2ab +b² =(a+b)² -
в) = ( (4a+(a-1)²)/(a-1)(a+1) ) *2a/(a+1) - (a(a+1)+a)/(a² -1)=
((a+1)²/(a-1)(a+1)) *2a/(a+1) - (a² +2a)/(a² -1) =2a/(a-1) - (a² +2a)/(a² -1) =
( 2a(a+1) -(a²+2a) )/(a² -1) =a²(a² -1)
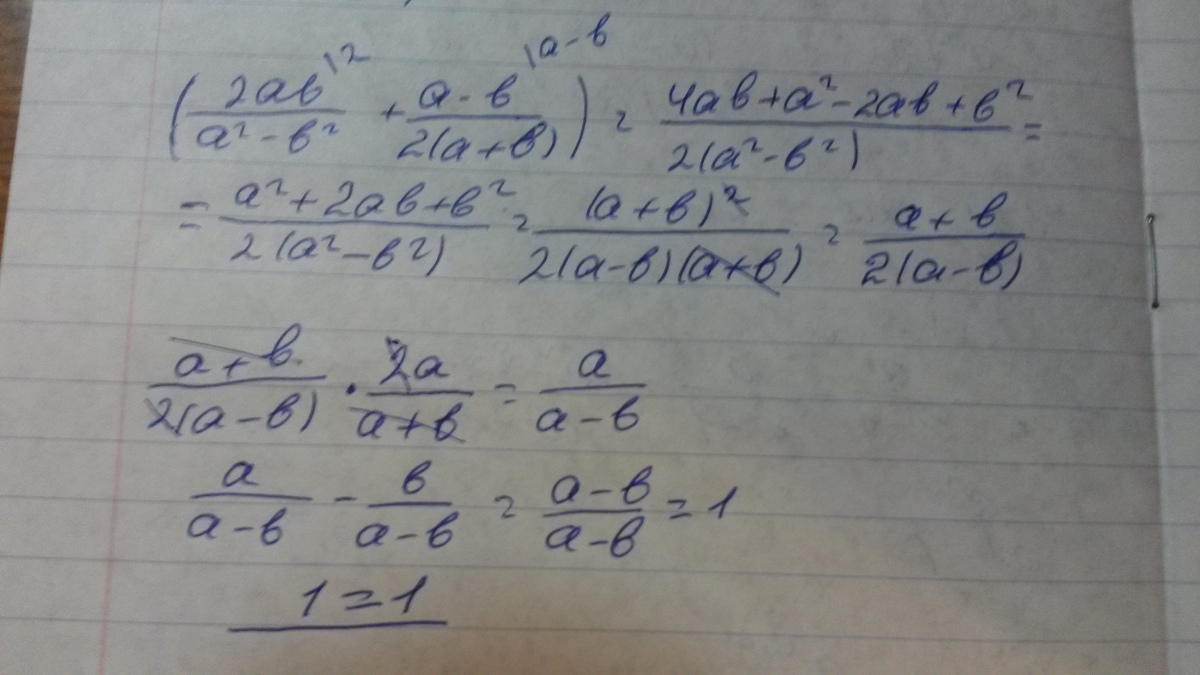
Cos t : ctg t = sin t
как доказать тождество
Решение: Ctg t = (cos t)/(sin t)
cos t : ctg t =cos t : (cos t)/(sin t) =
При деление дробь переворачивается
=cos t * (sin t)/(cos t) =
сокращаем cos t, получаем
=sin t
cos t : ctg t =cos t : (cos t)/(sin t) =cos t * (sin t)/(cos t)=sin t
Что и требовалось доказать.
Т к ctg t=sin t/cos t то получим cost:sint/cost=cos t*sin t/cos t=sin t
а sin t=sin t тождество доказанна
Доказать тождество:
б) ax-2by+ay-2bx=(a-2b)(x+y) 7класс
Решение: Приведем левую часть тождества
=(ах+ау)-(2ву+2вх)=а(х+у)-2в(х+у)=(а-2в)(х+у)
(а-2в)(х+у)=(а-2в)(х+у)Сначала выписываем левую часть, выносим общие множители за скобку. и у нас получается что левая часть = правой, следовательно, тождество верное!