тождество »
как доказать тождество - страница 31
Необходимо доказать тождество: \( \frac{1+sin2\alpha}{cos2\alpha}=tg(\frac{\pi}{4}+\alpha) \)
Решение: Решение
Применены : основное тригонометрическое тождество, формула квадрата суммы, формула сложения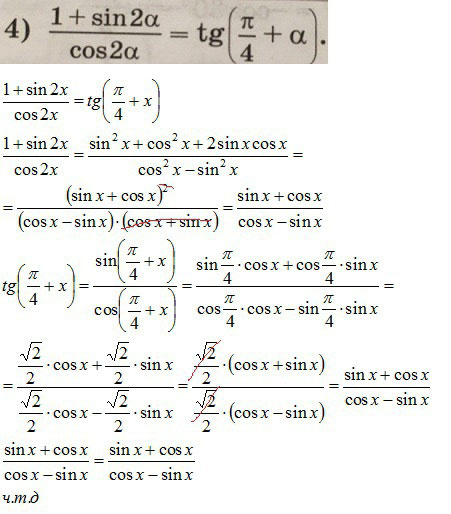
нужно доказать тождество \( \frac{1+td\alpha}{1+ctg\alpha}=tg\alpha \)
Решение: Используем свойство что tgA*ctgA = 1(1 + tgA) / (1 + ctgA) = (tgA*ctgA + tgA) / (1 + ctgA) = tgA*(ctgA + 1) / (1 + ctgA) = tgA

Доказать тождество:
(2n+1)2*-8n=(2n-1)2*
P.S. * это степень)
Решить задачу:
Одна сторона прямоугольника на 10% больше другой. Найти стороны, если периметр прямоугольника 84 см.
Решение: (2n+1)^2-8n=(2n-1)^2
4n^2+4n+1-8n=4n^2-4n+1 (по формуле сокр. умножения)
4n^2-4n+1=4n^2-4n+1, ч. т. д
периметр (P)=2(a+b)
2(a+b)=84
a+b=42
если а на 10% больше b, тогда a - 60%, b - 40%
42/100*60=25.2 см - сторона a
42-25.2=16.8 см - сторона b
ответ: 25.2 см, 16.8 см
4n2*+1-8n=4n2*+1-4n
4n2*+1-4n-4n2*-1+4n=0
0=0Доказать тождество: (4sina cosa)/(cos^2a-sin^2a)=2tg2a
Решение: $$ \frac{4\sin \alpha \cos \alpha}{\cos^2\alpha-\sin^2\alpha}=2tg2\alpha\ \ |(:2)\\\\\\ \frac{2\sin\alpha\cos\alpha}{\cos^2\alpha-\sin^2\alpha}= \frac{2}{ctg\alpha-tg\alpha} \\\\\\ \frac{2\sin\alpha\cos\alpha}{\cos^2\alpha-\sin^2\alpha}= \frac{2}{ \frac{\cos\alpha}{\sin\alpha}- \frac{\sin\alpha}{\cos\alpha}}\\\\\\ \frac{2\sin\alpha\cos\alpha}{\cos^2\alpha-\sin^2\alpha}= \frac{2}{ \frac{\cos^2\alpha-\sin^2\alpha}{\sin\alpha\cos\alpha}}\\\\\\ \frac{2\sin\alpha\cos\alpha}{\cos^2\alpha-\sin^2\alpha}=\frac{2\sin\alpha\cos\alpha}{\cos^2\alpha-\sin^2\alpha} \\ \boxed{tg 2\alpha= \frac{2tg\alpha}{1-tg^2\alpha} = \frac{2ctg\alpha}{ctg^2\alpha-1}= \frac{2}{ctg\alpha-tg\alpha} } $$
Можно доказать тождество проще:
$$ \frac{4\sin\alpha\cos\alpha}{\cos^2\alpha-\sin^2\alpha}=2tg2\alpha\\\\ \frac{2\sin2\alpha}{\cos2\alpha}=2tg2\alpha\\\\ 2tg2\alpha= 2tg2\alpha $$
Нужно доказать тождество \( \frac{2sin2α -sin4α}{2sin2α +sin4α}= tg²α \)
Решение: 2sin2α -sin4α= tg²α
2sin2α +sin4α
2sin2α-sin4α = 2sin2α -sin(2*2α) = 2sin2α -2sin2α cos2α =
2sin2α+sin4α 2sin2α +sin(2*2α) 2sin2α +2sin2α cos2α
= 2sin2α(1 -cos2α) = 1-cos2α = 1-(cos²α - sin²α) =
2sin2α(1 +cos2α) 1+cos2α 1+(cos²α - sin²α)
= 1-cos²α+sin²α = sin²α+sin²α = 2sin²α = sin²α = tg²α
1+cos²α-sin²α cos²α+cos²α 2cos²α cos²α
tg²α = tg²α - тождество доказано.