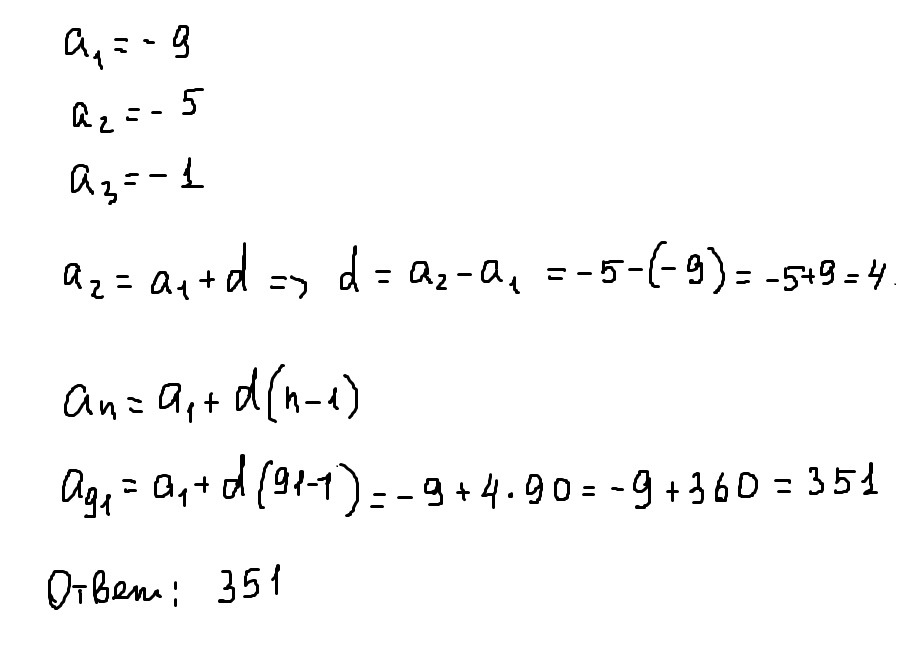n член арифметической прогрессии - страница 2
наидите число членов арифметической прогрессии
а1, а2, а2n, если а2+а4+а6+.+а2n=126 и an-2+an+4=42
Решение: $$ a_{2}+a_{4}+a_{6}+.a_{2n}=126\\ a_{n-2}+a_{n+4}=42 $$
теперь первое условие можно записать как
$$ n(a_{1}+nd)=126 $$
второе условие можно записать как
$$ 2a_{1}+(n-3)d+(n+3)d=42\\ 2a_{1}+2nd=42\\ a_{1}+nd=21 $$
теперь учитывая первое равенство получаем при делений первого на второе
$$ na_{1}+n^2d=126\\ a_{1}+nd=21\\ \\ \frac{na_{1}+n^2d}{a_{1}+nd}=6\\ \frac{n(a_{1}+nd)}{a_{1}+nd}=6\\ n=6 $$
Ответ 6Найдите число членов арифметической прогрессии \(а_1, а_2, а_{2n}, \;\;\;если\;\;\; а_2+а_4+а_6+...+а_{2n}=126 и a_{n-2}+a_{n+4}=42\)
Решение: $$ a_{2}+a_{4}+a_{6}+.a_{2n}=126\\ a_{n-2}+a_{n+4}=42\\\\ $$
теперь первое условие можно записать как
$$ n(a_{1}+nd)=126\\ $$
второе условие можно записать как
$$ 2a_{1}+(n-3)d+(n+3)d=42\\ 2a_{1}+2nd=42\\ a_{1}+nd=21 $$
теперь учитывая первое равенство получаем
$$ na_{1}+n^2d=126\\ a_{1}+nd=21\\ \\ \frac{na_{1}+n^2d}{a_{1}+nd}=6\\ \frac{n(a_{1}+nd)}{a_{1}+nd}=6\\ n=6 $$
Ответ 6
Выписаны несколько членов арифметической прогрессии: -9;-5;-1. Какое число стоит на 91 месте?
Решение: A1=-9 d=-5-(-9)=4
a91=a1+90d=-9+90*4=-9+360=351
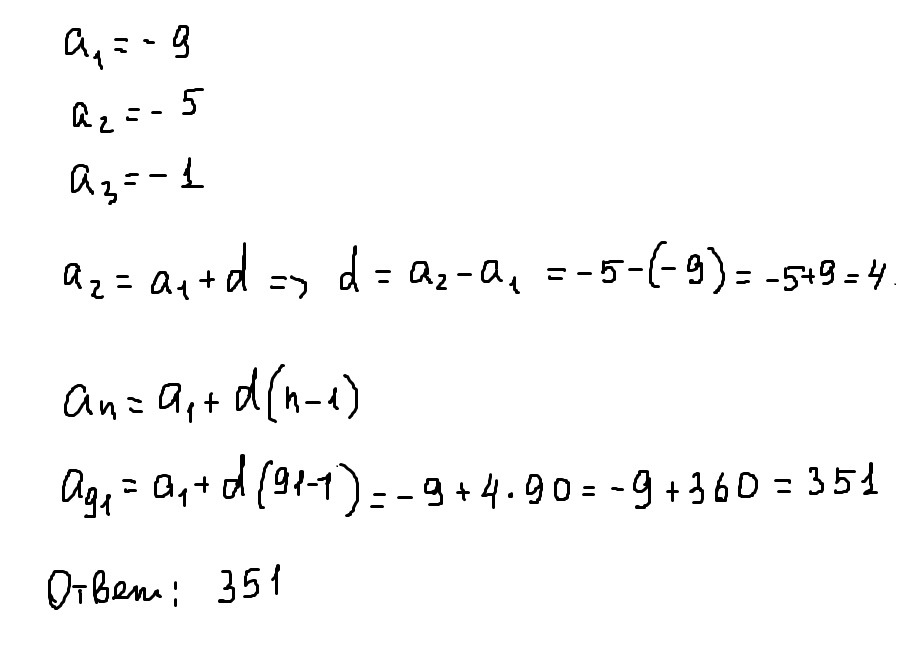
Виписали 20 членов арифметической прогрессии:6,5;8;. встретится ли среди них число 36
Решение: Если принять 18 за а1 и 4 за а2. то
находим д прогрессии =-14.
составляется ( по определению прогрессии арифм. 0 формула ан. те формула любого члена:
ан=а1-14*(н-1)
в конкретном данном случае получаем: 18+14-14н= 32-14н
для проверки принадлежности некоторого числа данной прогрессии число подставляется в роли ан и решается ураввнение относительно н - если в итоге преобразований и окажется натуральним числом, то число из этой команды.
не натуральное- извините. вы нам не подходите. :)))
Пример: -42 =32-14н 14н=74 н =74/14=37\7 увы. нацело не делитсяНет не встретится, максимальное число которое там встретится 16
выписали 30 членов арифметической прогрессии: 16, 18, встретятся ли среди них(и если да, то на каком месте) число: а) 38; б) 53; в) 70?
Решение: d=18-16=2Найдем последний 30-й член прогрессии по формуле an=a1+d(n-1):
а30=16+2*29=84
Т. к. максимальный член больше 70, то в этой прогрессии встретим числа 38 и 70, но не встретим 53, т. к. разность прогрессии - четное число и первый член прогрессии - четное число.
Найдем, какими по порядку членами являются числа 38 и 70 (из формул выше).
16+2(n-1)=38
2n-2=38-16=22
2n=22+2=24
n=12, т. е. число 38 - 12-й член прогрессии
16+2(n-1)=70
2n-2=70-16=54
2n=54+2=56
n=28, т. е. число 70 - 28-й член прогрессии
a₁=16
d=18-16=2
a) 16+2(n-1)=38
16+2n-2=38
14+2n=38
2n=38-14
2n=24
n=12
Число 38 является членом арифметической прогрессии и стоит на 12 месте
б) 16+2(n-1)=53
16+2n-2=53
14+2n=53
2n=53-14
2n=39
n=19,5
Число 53 не является членом арифметической прогрессии
в) 16+2(n-1)=70
16+2n-2=70
14+2n=70
2n=70-14
2n=56
n=28
Число 70 является членом арифметической прогрессии и стоит на 28 месте