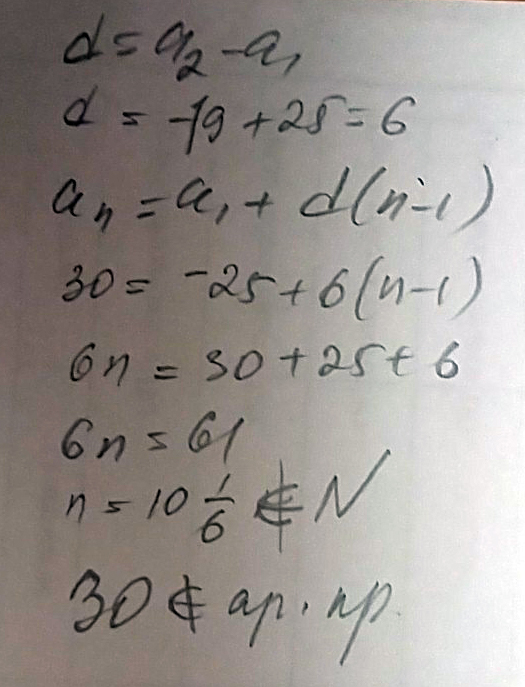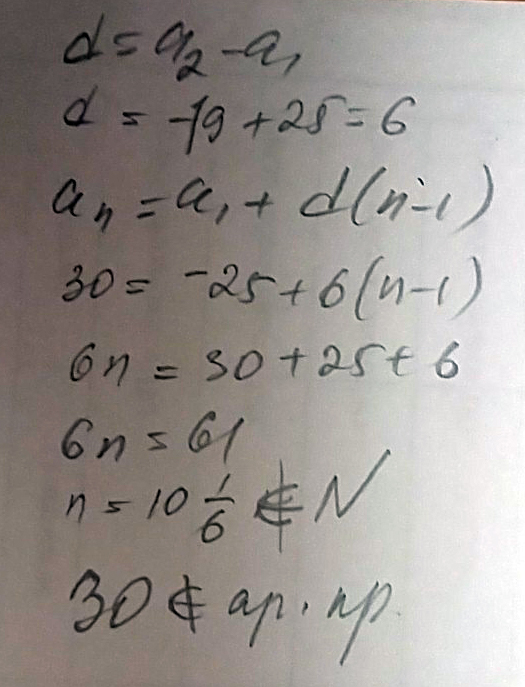n член арифметической прогрессии - страница 4

Является ли число -86 членом арифметической прогрессии в которой a1=-1 и a10=46?

а10=а1+9*d

Имея значения а1 и а10, выразим разность арифметической прогрессии d:

46=-1+9*d

$$ d=\frac{47}{9} $$

Обозначим номер члена данной арифметической прогрессии, который равен 86, за n. Тогда:

86=a1+d*(n-1)

Выразим искомое n, подставляя значения a1 и d:

$$ 86=-1+\frac{47}{9}*(n-1) $$

$$ n-1=\frac{87*9}{47} $$

$$ n=16\frac{31}{47}+1=17\frac{31}{47} $$

Т. к. n получилось нецелым числом, то число 86 не является членом данной арифметической прогрессии.

Ответ: не является.

является ли число 39 членом арифметической прогрессии если с1=-6 с9=6

c[9]=6

c[n]=c[1]+(n-1)*d

c[9]=c[1]+8d

d=(c[9]-c[1])/8

d=(6-(-6))/8=12/8=1.5

39=c[1]+(x-1)*d

39=-6+(x-1)*1.5

39+6=1.5*(x-1)

45=1.5*(x-1)

x-1=45/1.5

x-1=30

x=30+1

x=31

да 39 является 31 членом данной арифметической последовательности

является, т. к. с9=с1+d·(n-1)

  6= -6 +d· (9-1)

  -6 + d·8 = 6

  8d= 6+6

  d=12: 8

  d=1,5

  Cn=C1+d·(n-1)

  39= -6 + 1,5 · (N-1)

  -6 + 1,5N - 1,5 =39

  1,5N =39+1,5 + 6

  1,5N =46,5

  N= 31

С31=39, является, у него порядковый номер 31 (у члена прогрессии 39 )

Является ли число 39 членом арифметической прогрессии (Сn), в которой С1= -6 и С9=6

6= -6 + d· (9-1)

-6 + 8d = 6

 8d=6+6

8d=12

d= 12:8= 1,5

Cn= C1+d·(n-1)

39= -6 + 1,5 · (n-1)

-6 + 1,5 n -1,5 = 39

1,5 n = 39+1,5 +6

1,5 n = 46,5

n= 46,5 : 1,5=465: 15

n= 31

да, является число 39 членом данной прогрессии, и стоит порядковым номером 31

С31=39 

$$ d=\frac{c_9-c_1}{9-1}=\frac{6-(-6)}{8}=\frac{12}{8}=1,5 $$

$$ c_n=c_1+(n-1)\cdot d=-6+(n-1)\cdot1,5=-6+1,5n-1,5=1,5n-7,5 $$

$$ 39=1,5n-7,5 $$

$$ 1,5n=39+7,5 $$

$$ 1,5n=46,5 $$

$$ n=46,5:1,5 $$

$$ n=31 $$

$$ 39=c_{31} $$

Ответ: да, является.

Является ли число 156 членом арифметической прогрессии 2;9.

2+7=9

9+7=16

16+7=23

23+7=30

30+7=37

37+7=44

44+7=51

51+7=58

58+7=65

65+7=72

72+7=79

79+7=86

86+7=93

93+7=100

100+7=107

107+7=114

114+7=121

121+7=128

128+7=135

135+7=142

142+7=149

149+7=156

таким образом арифметическая прогрессия такая: 2,9,16,23,30,37,44,51,58,65,72,79,86,93,100,107,114,121,128,135,142,149,156

Является ли число 30 членом арифметической прогрессии -25:-19:.