прогрессия »

n член арифметической прогрессии - страница 5

  • Является ли число 12 членом арифметической прогрессии 18,15,12,


    Решение: A1 = - 18

    A2=  - 15

    разность = 3

    An=A1+b(n-1)=12

    -18+3(n-1)=12

    3n-3=30

    3n=33

    n=11

    Ответ, да является 11 членом

    Это вообще не арифметическая пргорессия. Проверь данные. Там должно быть так: -18,15,12,

    Если это так, то да, 12 является членом этой арифметической прогрессии.

  • Является ли число -59 членом арифметической прогрессии, если a1=21,d=-4?


    Решение: Нужно просто поставить в формулу известные значения. Номер никак не может быть дробью или отрицательным числом. Число 21, соответственно, может:)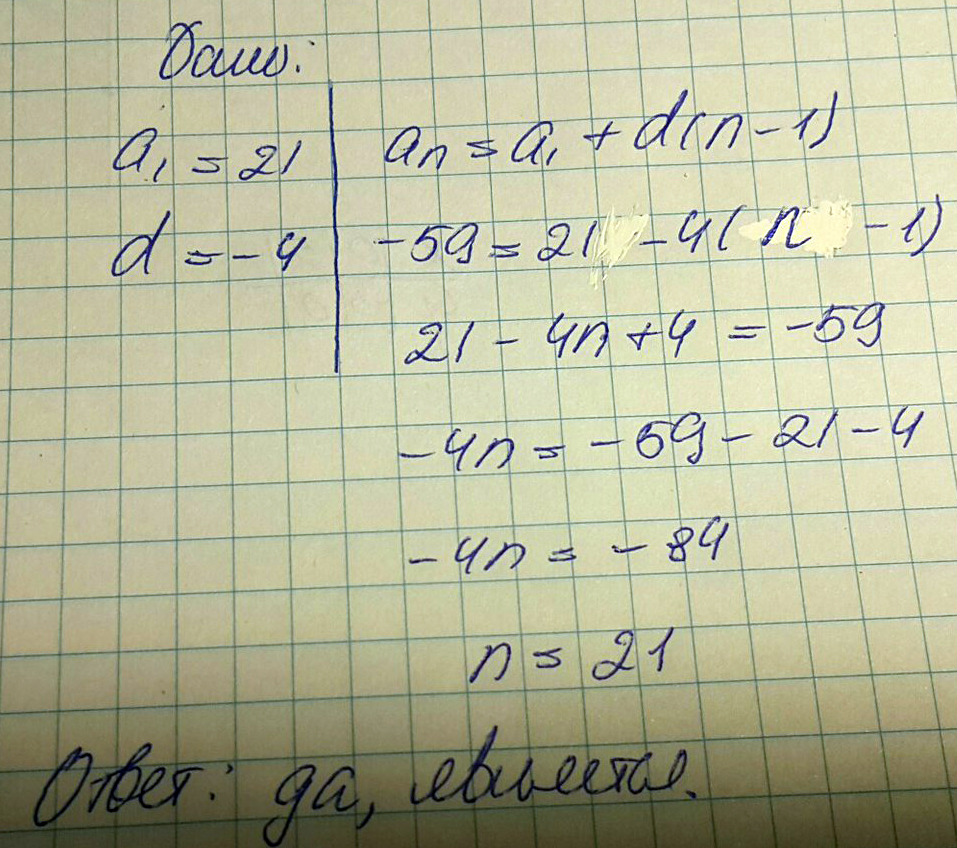

    Нужно просто поставить в формулу известные значения. Номер никак не может быть дробью или отрицательным числом. Число  соответственно может...

  • является ли число -6 членом арифметической прогрессии Сn в которойС1=30, С7=21?


    Решение: Находим d из равенства С7=С1+6d, d=-1,5, составляем уравнение для числа (-6) : -6=30+(n-1)(-1,5), где n-номер этого элемента,3n=-75, n=25, и -6 является 25-м членом прогрессии.

    Для арифметической прогрессии сn=с1+d(n-1)

    тогда с7=с1+(7-1)d

    21-30=6d

    d=-1.5

    Для cn=-6 получим: -6=30+(n-1)(-1,5)

    -36=(n-1)(-1,5)

    n-1=24

    n=25

    -6 является 25-м членом прогрессии

  • Является ли число 39 членом арифметической прогрессии, в которой с1= -6, с9=6


    Решение: $$ c_1=-6 $$
    $$ c_9=6 $$
    $$ c_n=c_1+(n-1)*d $$
    $$ c_9=c_1+(9-1)*d=c_1+8d $$
    $$ d=(c_9-c_1):8 $$
    $$ d=(6-(-6)):8=1.5 $$
    значит разность прогрессии равна 1.5
    далее проверим является ли число 39 членом данной прогрессии
    $$ 39=c_1+(n-1)*d $$
    $$ 39=-6+(n-1)*1.5 $$
    $$ 39+6=1.5(n-1) $$
    $$ 45=1.5(n-1) $$
    $$ 90=3(n-1) $$
    $$ n-1=90:3 $$
    $$ n-1=30 $$
    $$ n=30+1=31 $$
    как видим n - натуральное, n=31, значит число 39 - 31-й член данной прогрессии
    отвте: да, является

  • Является ли число 35 членом арифметической прогрессии -47;-44;. В случае утвердительного ответа укажите номер.


    Решение: Из разности первых двух членов получаем, что d=a2-a1=-44+47=3. Предполржим, что 35 является n-м членом этой прогрессии, тогда:
    35=-47+3*(n-1)
    82=3*(n-1)
    82 не делится нацело на три, значит не существует подходящего натурального числа n, и стало быть предположение не верно и число 35 не является членом данной арифм. прогрессии.

<< < 345 6 7 > >>