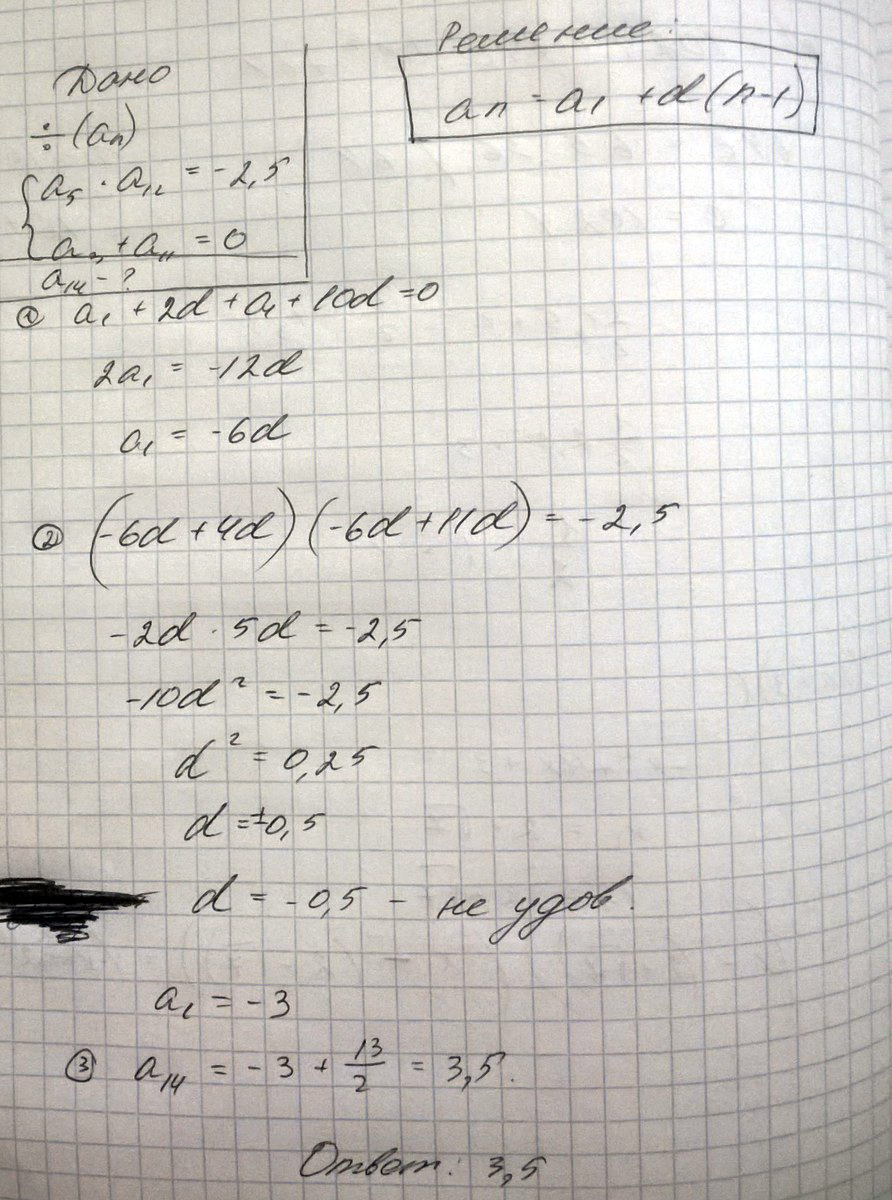прогрессия »

найти 3 члена арифметической прогрессии - страница 2

  • 1) Решить уравнение: 2 в степени 3х+5=(1/16) в степени 5-2х
    2) найти пятнадцатый член арифметической прогрессии, если сумма ее третьего и пятого членов равна 50, а сумма ее седьмого и одиннадцатого членов равна 80?


    Решение: 2^(3х+5)=(1/16)^( 5-2х)
    2^(3х+5)=(2)^( -4*(5-2х))
    3х+5= -4*(5-2х)
    3х+5= -20+8x
    5x=25
    x=5
    a3+a5=a1+2*d+a1+4d=2*a1+6*d=50
    a7+a11=2*a1+16*d=80
    ******************
    2*a1+6*d=50
    2*a1+16*d=80
    *************
    d=3
    a1=(50-6*3)/2=16
    *********
    a15=a1+14*d=16+14*3=58

    х - х х - - х х - - х х - x x x a a a d a d a d a a a d a d a d d a - a a d...

  • Сумма 3 и 9 членов арифметической прогрессии равна 6 а произведение равно 135/16 найти S15?


    Решение: Записываем формулу для третьего члена: А3 = А1 + 2d

    Записываем формулу для девятого члена: A9 = A1 + 8d

    Складывая, получаем:

    2А1 + 10d = 6 (по условию)

    (А1 + 2d)*(A1 + 8d) = 135/16

    Система из этих двух уравнений даст значения для A1 и d

    Затем их нужно будет подставить в формулу суммы первых 15 членов:

    S15 = 15*(2*A1 + 14d)/2

    Таким образом вы получите искомое значение суммы.

  • 6. Произведение пятого и двенадцатого членов возрастающей арифметической прогрессии равно -2,5, а сумма третьего и одиннадцатого членов равна нулю. Найти a14.


    Решение: A₅*a₁₂=-2,5 (a₁+4d)*(a₁+11d)=-2,5 (-6d+4d)*(-6d+11d)=-2,5 
    a₃+a₁₁=0     a₁+2d+a₁+10d=0         2a₁=-12d    a₁=-6d  
    -2d*5d=-2,5  -10d²=-2,5  d²=0,25  d=+/-0,5
    Так как арифметическая прогрессия возрастающая, d=0,5
    a₁=-6d=-3 ⇒  a₁₄=a₁+13d=-3+13*0,5=-3+6,5=3,5.

    ___________________________

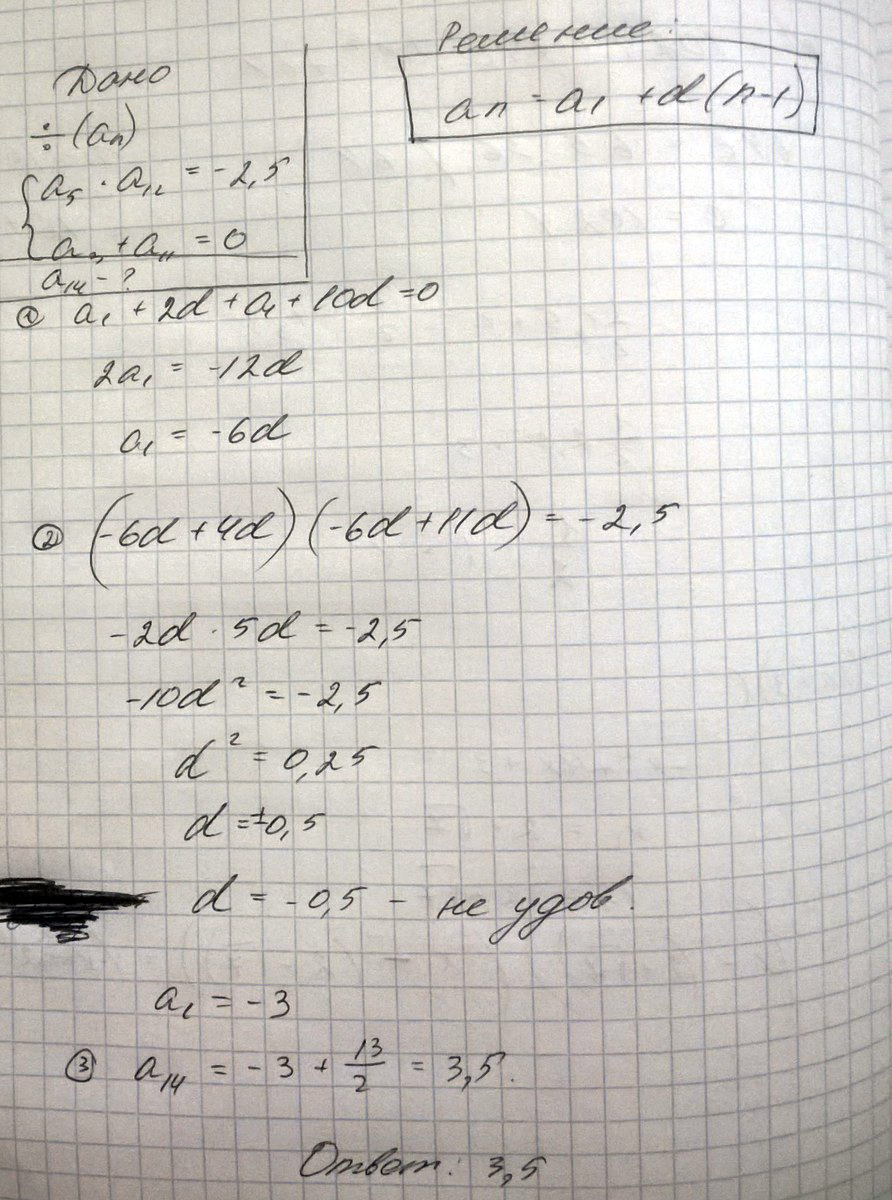
    A a -   a d a d - - d d - d d -  a a      a d a d          a - d    a - d  - d d -   - d -   d   d - Так как арифметическая прогрессия возрастающая d a - d -   a a d - - ....

  • Сума восьмого и двадцатого членов арифметической просрессии равна 48. Найти четырнадцатый член прогрессии.


    Решение: Пусть а8 - это первый член арифм прогрессии. тогда а20 будет 13 членом ариф прогресс.

     тогда полуится система: 

    а20=а8+d(13-1) а20-а8=12d

    а20+а8=48 a20+a8=48

    Сложим два выражения:

    2a20=48+12d

    a20=24+6d

    Отсюда полчаем, что a20 - это 7 член арифм прогрессии (6+1=7), тогда получаем, что в этом равенстве 24 - это 14 член арифм прогрессии ( 20-6=14 ). т. е. а14=24

  • 4. Дана арифметическая прогрессия (an):
    -148; -143,8; -139,6; -135,4,
    Найти номер наименьшего положительного члена прогрессии.
    5. По условию задания 4 найти сумму наименьшего положительного и наибольшего отрицательного членов прогрессии.


    Решение: Формула арифметической прогрессии : a_n = a_1+d(n-1), где d - разность геометрической прогрессии, а n - номер члена арифметической прогрессии. В нашей арифметической прогрессии a_1 = -148, a_2=-143.8, a_3 = -139.6 и т. д. 
    Найдём разность по формуле d=a_2 - a_1 d=-143,8 - (-148) = 4,2
    Арифметическая прогрессия возрастает от -148, до бесконечности положительных чисел.
    Первое положительное число будет стоять сразу после 0. Значит a_n >1 / Составим неравенство
    a_1 + d(n-1)>1
    d(n-1)>1-a_1
    n-1>1-(a_1:d)
    n>1-(a_1:d)+1
     n>2-(a_1:d)
    Подставляем числа
    n>2 - (-148:(-4.2)
    n> 37,238
    Значит мы можем сделать вывод, что наименьшее положительное число имеет 37 номер. 
    Давайте найдём его.a_37 = a_1 + d(37-1) = a_1+36d=-148 + 36 * 4.2=3,2 - наименьший положительный член прогрессии. Сразу же можем найти наибольший отрицательный член прогрессии 3.2 - 4.2 = -1. А сумма наибольшего с наименьшим равна -1 + 3.2 = 2.2 

<< < 12 3 4 > >>