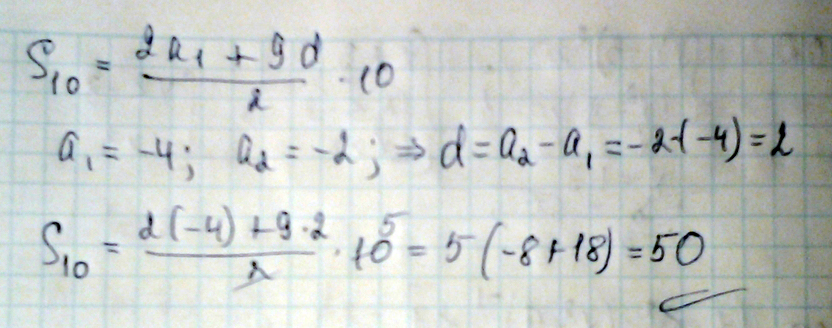прогрессия »

дана арифметическая прогрессия

  • Дана арифметическая прогрессия, в которой а2а5=112 а1\а5 =2. составить формулу n-ого члена прогрессии и определите, сколько в данной прогрессии членов, модуль которых не превосходит 10


    Решение: A₂*a₅=112 (a₁+d)(a₁+4d)=112  a₁²+5a₁d+4d²=112
    a₁/a₅=2    a₁-2*(a₁+4d)=0  a₁-2a₁-8d=0  a₁=-8d
    (-8d)²+5*(-8d)*d+4d²=112
    64d₂-40d²+4d²=112
    28d²=112
    d²=4
    d₁=-2  d₂=2  d₂∉ так как прогрессия убывающая (а₁/а₅=2) ⇒
    a₁=-8*(-2)=16  
    an=a₁+(n-1)*d
    an=16+(n-1)*(-2)
    an=16-2*(n-1)
    an=16-2n+2
    an=18-2n.
    18-2n=I10I
    18-2n=10  2n=8   n=4
    18-2n=-10   2n=28  n=14.

  • Дана арифметическая прогрессия. Найдите а51\а15, если известно, что а3\а9=4?


    Решение: По условию а3/а9 = 4, 

    Или (а1+2d)/(a1+8d) = 4.

    Разделим и числитель, и знаменатель на d:

    (t+2)/(t+8) = 4, где t = a1/d. Решим это уравнение:

    t+2 = 4t+32. t= - 10:

    а51/а15 = (а1+50d)/(a1+14d) = (t+50)/(t+14) = 10.

    Ответ: 10.

    a3/а9=(а1+2d)/(а1+8d)=4

    a1+2d=4a1+32d

    a1=-10d

    a51/а15=(a1+50d)/(а1 + 14d)= (-10d+50d)/ (-10d+14d) = 40d/4d= 10

    Ответ: 10. 

  • Дана арифметическая прогрессия:
    -4;-2;0.
    Найдите S10-


    Решение: А1=-4;
    а2=-2;
    а3=0;
    d=a2-a1=-2+4=2;
    S10=2a1+d(n-1)/2*10.
    дальше просто в формулу поставляем известные значения и всё! :)

    Применена формула суммы арифметической прогрессии

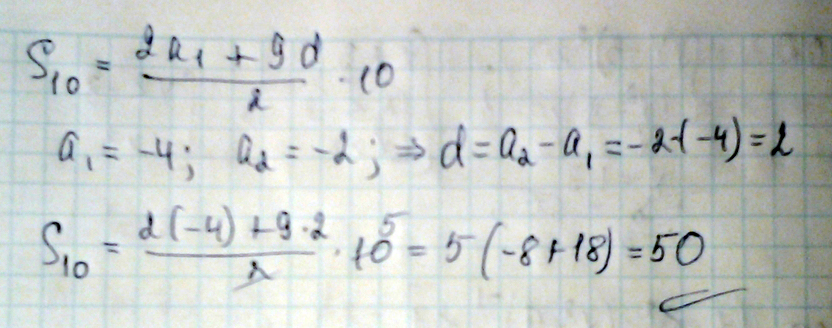
    А - а - а d a -a - S a d n- .дальше просто в формулу поставляем известные значения и вс Применена формула суммы арифметической прогрессии...

  • Дана арифметическая прогрессия (аn) : -1.4; 0.5; 2.4. найдите а21


    Решение: Любой n-ный член прогрессии можно найти по формуле an=a1+d*(n-1), где an- n-ный член прогрессии, который сейчас и будем искать, а1=-1,4 - первый член прогрессии (именно -1,4 у вас стоит на первом месте), d-разность арифм. прогрессии - разность между следующим членом и предыдущим, например между вторым и первым, четвертым т третьим и т. д. в данном случае возьму d=a2-a1=0,5 - (-1,4)=1,9
    n - номер члена прогрессии, который ищем, в данном случае n=21, тогда получим а21=-1,4 +1,9*(21-1)=-1,4 +1,9*20=36,6

  • Дана арифметическая прогрессия (an), для которой а6 = -7.8, a19 = -10.4. Найдите разность прогрессии.


    Решение: Решение:
    an=a1+d(n-1)
    Согласно этой формуле:
    a6=a1+d(6-1)
    a19=a1+d(19-1)  Подставим в эти выражения а6 и а19, получим систему уравнений:
    -7,8=a1+5d
    -10,4=a1+18d  Из первого уравнения  найдём а1 и подставим во второе уравнение:
    а1=-7,8-5d
    -10,4=(-7,8-5d)+18d
    -10,4=-7,8-5d+18d
    13d=-10,4+7,8
    13d=-2,6
    d=-2,6/13=-0,2
    Ответ: разность прогрессии d= - 0,2

1 2 3 > >>