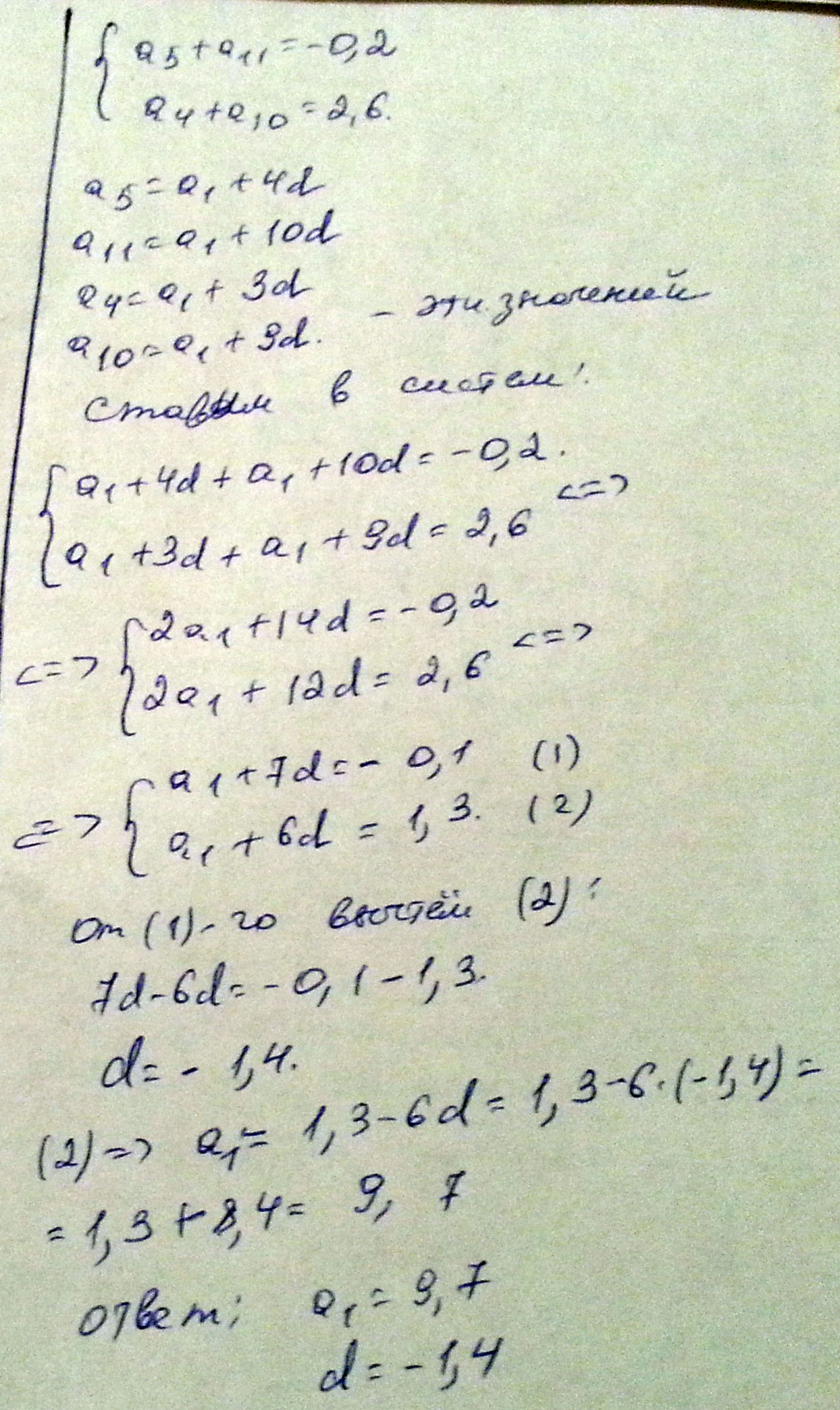прогрессия »

найти первый член и разность прогрессии - страница 22

  • Найдите первый член и разность арифметической прогрессии.
    {а5+а11=-0,2,
    {а4+а10=2,6.


    Решение: А5=а1+4d a11=a1+10d a4=a1+3d a10=a1+9d
     { a1+4d+a1+10d=-0.2
      a1+3d+a1+9d=2.6
      { 2a1+14d=-0.2
      2a1+12d=2.6 ( *-1)
      {2a1+14d=-0.2
      -2a1-12d=-2.6
      {2d=-2.8 { d=-1.4 {d=-1.4
      2a1+14d=-0.2 a1+7d=-0.1  a1=-0.1-7*-1.4=-0.1+9.8=9.7
      ответ -1,4- разность 9,7 1 член

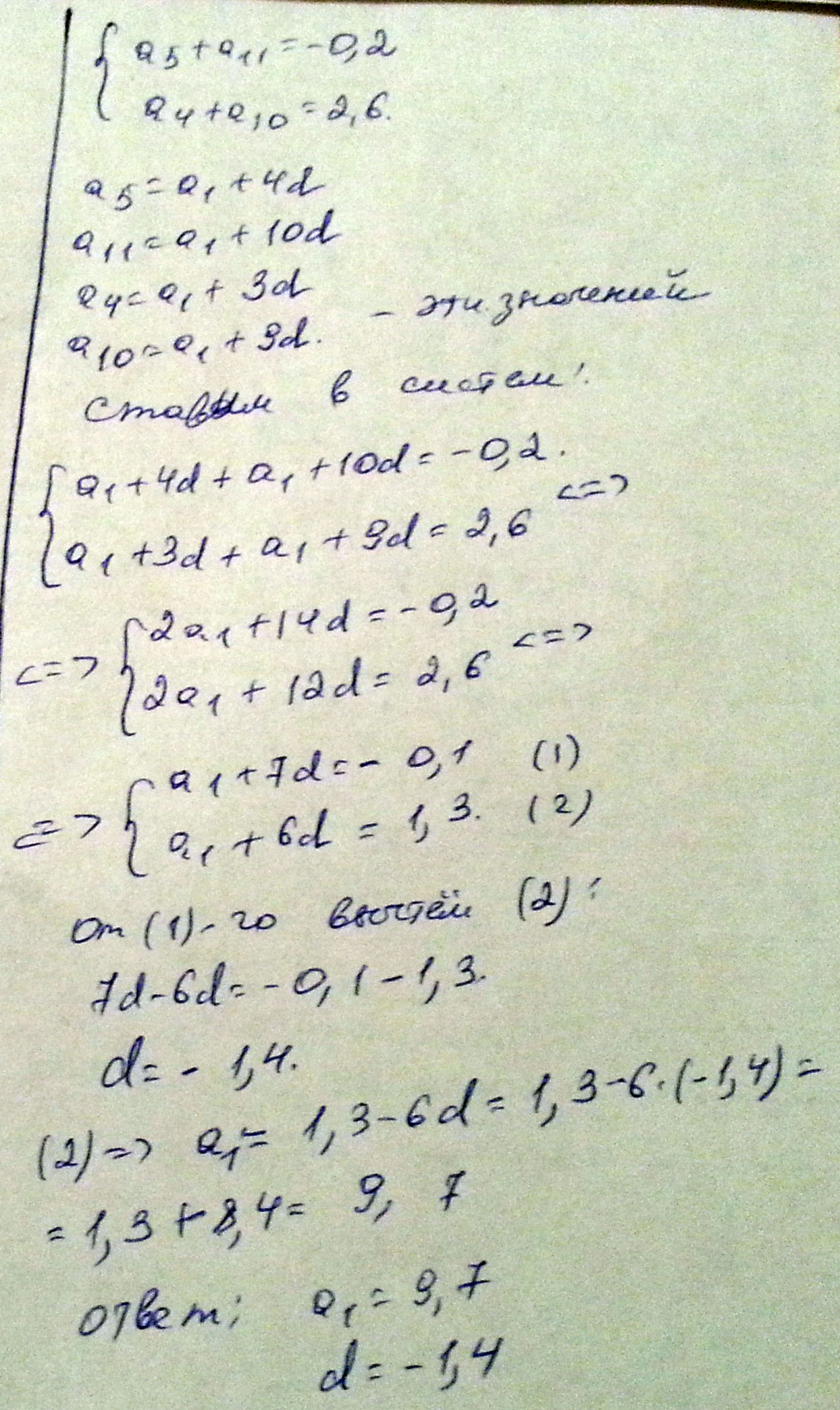
    А а d a a d a a d a a d  a d a d - .   a d a d .   a d - .   a d . -   a d - .   - a - d - .   d - . d - . d - .   a d - . a d - .   a - . - - . - . . .   ответ - - разность...

  • Найдите первый член и разность арифметической прогрессии (ап), если а1+а6=-12; а5-а2=-9


    Решение: 1). а1+а6=-12

    а6=а1+5d

    Получаем: а1+а1+5d=-12

    2а1+5d=-12 

    а1=-12-5d\2 

    2). а1-а2=-9

    а2=а1+d

    Получаем: а1-(а1+d)=-9

    а1-а1-d=-9

    d=9

    Мы нашли d. Это разность арифметической прогрессии. Подставляем в 1-ю формулу:

    а1=-12-5*9\2=-12-45\2= -57\2=-28,5

    a1+a6=-12 a1+a1+5d=-12 2a1=3 a1=1.5
    a5-a2=-9 a1+4d-(a1+d)=-9 3d=-9 d=-3

     

  • Найдите первый член и разность арифметической прогрессии
    а) 0,7, 0,9, 1,1, 1,3,
    б) -1,0,9,0,8, 0,7,


    Решение: А) разность арифметической прогресси 0,9-0,7=0,2. Находится по формуле d= an+1-an, где d-разноть, a-член (или обозначение) арифметической прогрессии, n- номер.
    б) -0,9-(-1)= -0,9+1=0,1. 
    А первый член арифметической прогрессии обычно пишется в начале, т. е в первом случае это 0,7, а во втором -1.

  • Найдите первый член и разность арифметической прогрессии (an), если а7+а3=-8, а8-а5=-6


    Решение: \({a_n} \) -  арифметическая прогрессия
    $$ a_n=a_1+(n-1)d \\ a_7=a_1+6d \\ a_3=a_1+2d \\ a_8=a_1+7d \\ a_5=a_1+4d \\ \left \{ {{a_7+a_3=-8} \atop {a_8-a_5=-6}} \right. \\ \left \{ {{a_1+6d+a_1+2d=-8} \atop {a_1+7d-a_1-4d=-6}} \right. \\ \left \{ {{2a_1+8d=-8} \atop {3d=-6}} \right. \\ \left \{ {{a_1+4d=-4} \atop {d=-2}} \right. \\ \left \{ {{a_1=-4-4d} \atop {d=-2}} \right. \\ \left \{ {{a_1=-4-4*(-2)} \atop {d=-2}} \right. \\ \left \{ {{a_1=4} \atop {d=-2}} \right. $$

  • Найдите первый член и разность арифметической прогрессии (Хn) если х16 = -7 и х26 = 55


    Решение: Пусть \(x_{1}\) - первый член прогрессии, а d - разность.

    общая формула n-ого члена арифметической прогрессии: $$ x_{n}=x_{1}+d(n-1) $$

    тогда: $$ x_{16}=x_{1}+15d \\ x_{26}=x_{1}+25d $$

    получим систему: $$ \left \{ {{x_{1}+15d=-7} \atop {x_{1}+25d=55}} \right. $$

    вычтем из первого уравнения второе, получим -10d=-62. получим d=6,2.

    подставим в первое уравнение: $$ x_{1}+15*6,2=-7 \\ x_{1}+93=-7 \\ x_1=-100 $$

<< < 202122 23 24 > >>