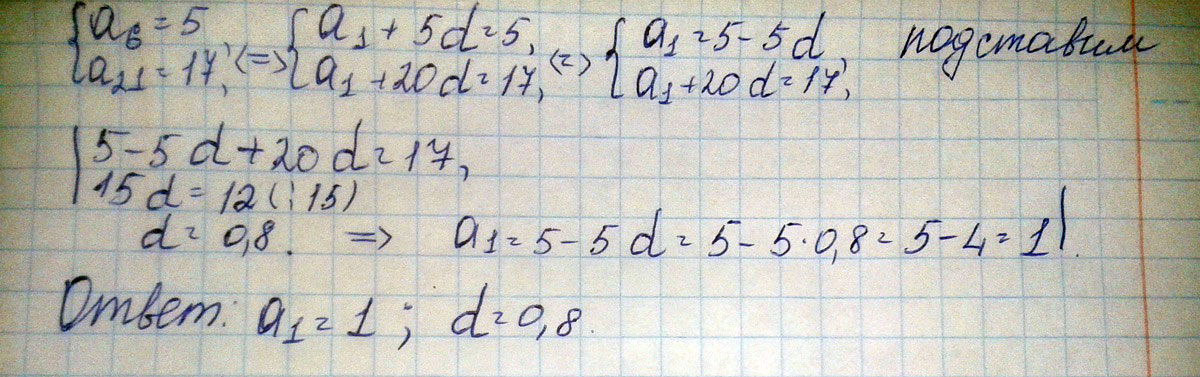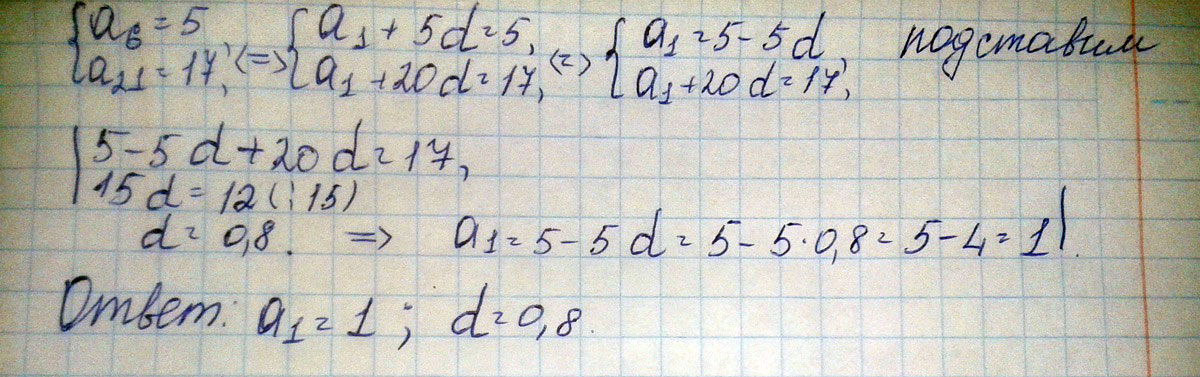прогрессия »
найти первый член и разность прогрессии - страница 20
Вычислите сумму корней уравнения: (см вложение)
2) Найти разность ар-й прогресси, если a15 =21 и S14=84
-
3) Мальчик и девочка шагами измеряли одно и то же расстояние в 1152 м. Сколько раз их следы совпали если шаг парня 72см, а шаг девушки 64 см?
Решение: Вычислите сумму корней уравнения:
x*корень(3)/(2*корень(3)-х) = x*2/(5-корень(3)*х)
x*корень(3)/(2*корень(3)-х) - x*2/(5-корень(3)*х) = 0
x*(корень(3)/(2*корень(3)-х) - 2/(5-корень(3)*х)) = 0
x1=0 или корень(3)/(2*корень(3)-х) - 2/(5-корень(3)*х) = 0
корень(3)/(2*корень(3)-х) - 2/(5-корень(3)*х) = 0
{корень(3)(5-корень(3)*х) -2(2*корень(3)-х) }/ {(2*корень(3)-х) * (5-корень(3)*х)} = 0
корень(3)(5-корень(3)*х) -2(2*корень(3)-х) = 0
корень(3)*5-3*х - 4*корень(3)+2х = 0
x2=корень(3)
x1+x2=корень(3)
ответ корень(3)
2) Найти разность ар-й прогресси, если a15 =21 и S14=84
S14=a1+a2+.+a14 = (a15-14*d) + (a15-13*d) +.( a15-1*d) = 14*a15-(1+14)*14/2*d= 14*a15-105*d
d =( 14*a15 - S14)/105 = ( 14*21 - 84)/105 = 2 - это ответ
-
3) Мальчик и девочка шагами измеряли одно и то же расстояние в 1152 м.
Сколько раз их следы совпали если шаг парня 72см, а шаг девушки 64 см?
HOK(72;64)=HOK(9*8;8*8)=9*8*8
N=1152 / (9*8*8) + 1 = 3 - это ответ (следы совпали 3 раза включая стартовое положение )
Сумма первых 12арифметической прогресси равна 354ю отношение суммы членов, стоящих на черных местах среди первых 12, к сумме членов, стоящих на нечетных местах среди 12, равна32:27. найти разность этой погрессии
Решение: $$ S_{12}=\frac{2a_1+11d}{2}\cdot 12=354\\2a_1+11d=59 $$
По условию
$$ \frac{a_2+a_4+.+a_{12}}{a_1+a_3+.+A_{11}}=\frac{32}{27},\\a_2+a_4+a_6+a_8+a_{10}+a_{12}=(a_1+d)+(a_!+3d)+(a_1+5d)+(a_1+7d)+\\+(a_1+9d)+(a_1+11d)=6a_1+36d=6(a_1+6d),\\a_1+a_3+a_5+a_7+a_9+a_{11}=a_1+(a_1+2d)+(a_1+4d)+\\+(a_1+6d)+(a_1+8d)+(a_1+10d)=6a_1+30d=6(a_1+5d)\\\frac{32}{27}=\frac{6(a_1+6d)}{6(a_1+5d)}\\32(a_1+5d)=27(a_1+6d)\\5a_1-2d=0\\ \left \{ {{5a_1=2d} \atop {2a_1+11d=59}} \right. \\a_1=\frac{2d}{5}\\2\cdot\frac{2d}{5}+11d=59\\\frac{4d+55d}{5}=59, 59d=5\cdot 59, d=5 $$Найти первый член и разность арифметической прогрессии (bn) если b16= - 37 и b6= -7
Решение: Воспользуемся формулами n-го члена ар. прогрессии и составим и решим систему.аn=а1+d(n-1)
b16=b1+15d
b6=b1+5d
b1+15d=-37
b1+5d=-7
Решим систему способом сложения, для этого второе уравнение системы умножим на -1, получим:
b1+15d=-37
-b1-5d=7
10d = -30
d=-30:10
d=-3
b1+5d=-7
b1+5(-3) = -7
b1-15=-7
b1=-7+15
b1=8
ответ: b1=8; d=-3
Найти 6 член и разность арифметической прогрессии, если a5+a7=54
ещё a2= 39
Решение: 1) a5 = 2*5 - 5² = 10 - 25 = -15 (ответ 1) )
2) а6 = 2 + (6 - 1)*(-3) = 2 - 15 = -13 (ответ 3) )
3) d = a6 - a2 / 4 = 14-4 /2 = 2,5 (ответ 1) )
4) S10 = ( 2*2 + 9*4) / 2 * 10 = 200 (ответ 4) )
Повыш. уровень.
1) Прогрессия убывающая, с разностью d= - 0,2
Первый член равен 3,
посчитаем, каким по счету будет член, равный нулю. Обозначим его аn, аn=0.
3 : 0,2 = 15,
тогда по формуле аn = а1 + (n - 1)*d найдем n:
0 = 3 + 15*(- 0,2)
0 = 3 + (16 - 1)*(- 0,2)
значит а16 равен нулю, значит в последовательности 15 положительных членов.
2) а3 = 10 => 10 = a1 + 2d
а7 = 10 => 40 = a1 + 6d получили систему.
Из второго вычтем первое уравнение, получим:
30 = 4d => d = 7,5
a1 = 10 - 2d = 10 - 15 = -5
Тогда а5= a1 + 4d = -5 + 4*7,5 = 25
3) Если рассматривать множество натуральных чисел как арифм. прогрессию с первым членом a1 = 1 и разностью d = 1, то задача сводится к нахождению разности S100 - S39,
S100 = (1+100) /2 * 100 = 5050
S39 = (1+39) /2 * 39 = 780
S100 - S39 = 5050 - 780 = 4270
4) d = а8 - а4 / 4 = 20 - 8 /4 = 12/4 = 3
Тогда по формуле аn = а1 + (n - 1)*d найдем чему равен первый член:
а4 = а1 + (4 - 1)*d
8 = а1 + 3*3
а1 = -1
Тогда 16-й член будет равен: а16 = а1 + (16 - 1)*d = -1 + 15*3 = 44
Т. о. действительно такая ар. прогрессия существует и формула общего члена такая: аn = -1 + 3(n - 1) = -1 + 3n - 3 = 3n - 4
аn = 3n - 4
5) аn = 3n - 1
а1 = 3 - 1 = 2
а2 = 6 - 1 = 5
d = а2 - а1 = 5-2 = 3
S = S54 - S13 = 4401 - 260 = 4141
S54 = (2*2 + 53*3) /2 * 54 = (4 + 159) /2 * 54 = 163 * 54 /2 = 4401
S13 = (2*2 + 12*3) /2 * 13 = (4 + 36) /2 * 13 = 20 * 13 = 260
Ответ: сумма членов прогрессии с 14 по 54 включительно равна 4141.
Найти первый член и разность арифметической прогрессии, если а6=5 а 21=17
Решение: 17=а1+20д
5=а1+5д - система (вычитание)
12=15д
отсюда д=15\12=5\4
подставляем в любое ур-ие
а1+25/4=5
а1=(-5/4)
А6=5=А1+5d
А21=17=А1+20d
A1=5-5d
5-5d+20d=17
15d= 12(:15)
d=0.8
A1=5-5d=5-5*(0.8)=5-4=1